【数学】2014高考专题复习：第4章 三角函数及三角恒等变换 第2节 三角函数的图像和性质及三角恒等变换 205页

【数学】2014 版《6 年高考 4 年模拟》 第四章 三角函数及三角恒等变换 第二节 三角函数的图象和性质及三角恒等变换 第一部分 六年高考荟萃 2013 年高考题 一、选择题 1 ．（2013 年普通高等学校招生统一考试山东数学（理）试题（含答案））将函数 sin(2 )y x   的图象沿 x 轴向左平移 8  个单位后,得到一个偶函数的图象,则 的一个可能取值为 (A) 3 4  (B) 4  (C)0 (D) 4  答案：B 将函数 y=sin（2x + ）的图像沿 x 轴向左平移 8  个单位，得到函数 sin[2( ) ] sin(2 )8 4y x x        ，因为此时函数为偶函数，所以 ,4 2 k k Z      ，即 ,4 k k Z    ，所以选 B. 2 ．（2013 年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））已知函 数  =cos sin 2f x x x ,下列结论中错误的是 (A)  y f x 的图像关于 ,0 中心对称 (B)  y f x 的图像关于直线 2x  对称 (C)  f x 的最大值为 3 2 (D)  f x 既奇函数,又是周期函数 答案：C 对于 A 选项，因为 f（2π﹣x）+f（x）=cos（2π﹣x）sin2（2π﹣x）+cosxsin2x=﹣ cosxsin2x+cosxsin2x=0，故 y=f（x）的图象关于（π，0）中心对称，A 正确； 对于 B 选项，因为 f（π﹣x）=cos（π﹣x）sin2（π﹣x）=cosxsin2x=f（x），故 y=f（x）的 图象关于 x= 不对称，故 B 正确； 对于 C 选项，f（x）=cosxsin2x=2sinxcos2x=2sinx（1﹣sin2x）=2sinx﹣2sin3x，令 t=sinx ∈ [﹣ 1，1 ] ，则 y=2t﹣2t3，t ∈ [﹣1，1 ] ，则 y′=2﹣6t2，令 y′＞0 解得 ，故 y=2t﹣ 2t3，在[ ] 上增，在[ ] 与[ ] 上减，又 y（﹣1）=0，y（ ）=， 故函数的最大值为 ，故 C 错误； 对于 D 选项，因为 f（﹣x）+f（x）=+cosxsin2x+cosxsin2x=0，故是奇函数，又 f（x+2π） =cos（2π+x）sin2（2π+x）=cosxsin2x，故 2π是函数的周期，所以函数即是奇函数，又是周 期函数，故 D 正确。 综上知，错误的结论只有 C，故选 C 3 ．（2013 年普通高等学校招生统一考试山东数学（理）试题（含答案））函数 cos siny x x x  的图象大致为 答案： D 函数 y=xcosx + sinx 为奇函数，所以图象关于原点对称，所以排除 B，C.当 x  时， ( ) 0f     ,排除 A,选 D. 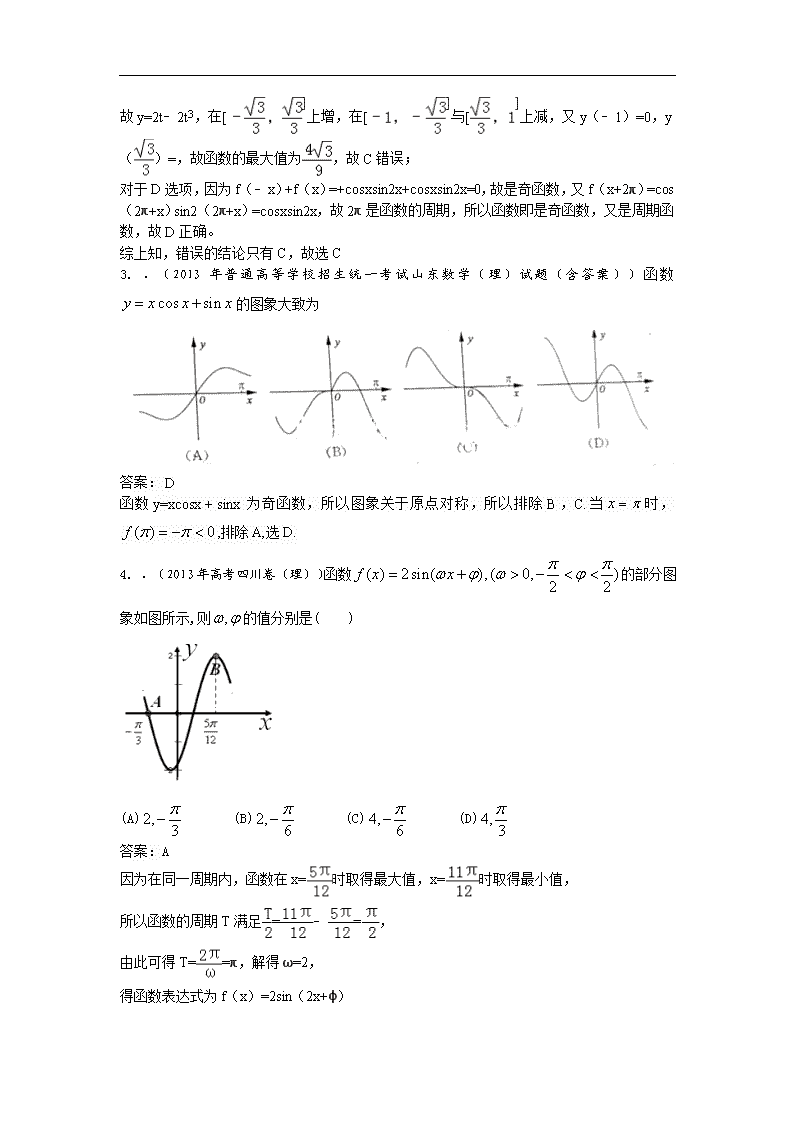4 ．（2013 年高考四川卷（理））函数 ( ) 2sin( ),( 0, )2 2f x x           的部分图 象如图所示,则 ,  的值分别是( ) (A) 2, 3  (B) 2, 6  (C) 4, 6  (D) 4, 3  答案：A 因为在同一周期内，函数在 x= 时取得最大值，x= 时取得最小值， 所以函数的周期 T 满足 = ﹣ = ， 由此可得 T= =π，解得ω=2， 得函数表达式为 f（x）=2sin（2x+φ） 又因为当 x= 时取得最大值 2， 所以 2sin（2• +φ）=2，可得 +φ= +2kπ（k ∈ Z） 因为 ，所以取 k=0，得φ=﹣ 。 选：A 5．（2013 年高考湖北卷（理））将函数  3cos siny x x x R   的图像向左平移  0m m  个长度单位后,所得到的图像关于 y 轴对称,则 m 的最小值是( ) A. 12  B. 6  C. 3  D. 5 6  答案：B 本 题 考 查 三 角 函 数 的 图 象 与 平 移 以 及 三 角 函 数 的 图 象 与 性 质 。 y= 3 cosx+sinx 2cos( )6x   ,将函数 2cos( )6y x   的图像向左平移 m（m＞0）个单位 长度后，得到 2cos( )6y x m    ，此时关于 y 轴对称，则 ,6m k k Z    ，所以 ,6m k k Z    ，所以当 0k  时，m 的最小值是 6  ，选 B. 二、填空题 6．（2013 年高考上海卷（理））已知△ABC 的内角 A、B、C 所对应边分别为 a、b、c,若 2 2 23 2 3 3 0a ab b c    ,则角 C 的大小是_______________(结果用反三角函数值表示) 答案： 1arccos 3C   7．（2013 年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯 WORD 版含附加题）） 函数 )42sin(3  xy 的最小正周期为___________. 答案： 2= =2T   8．（2013 年高考江西卷（理））函数 2sin 2 2 3siny x x  的最小正周期为T 为_________. 答案： 本 题 考 查 三 角 函 数 的 化 简 ， 以 及 三 角 函 数 的 图 象 和 性 质 。 2 1 cos2sin 2 2 3sin sin 2 2 3 sin 2 3 cos2 32 xy x x x x x        2sin(2 ) 33x    ，所以周期 2 2T    三、解答题 9．（2013 年高考陕西卷（理））已知向量 1(cos , ), ( 3sin ,cos2 ),2x x x x   a b R , 设函数 ( ) ·f x  a b . (Ⅰ) 求 f (x)的最小正周期. (Ⅱ) 求 f (x) 在 0, 2      上的最大值和最小值. 解:(Ⅰ) ( ) ·f x  a b = )62sin(2cos2 12sin2 32cos2 1sin3cos  xxxxxx . 最小正周期   2 2T . 所以 ),62sin()(  xxf 最小正周期为 . (Ⅱ) 上的图像知，在，由标准函数时，当 ]6 5,6-[sin]6 5,6-[)62(]2,0[  xyxx  . ]1,2 1[)]2(),6-([)62sin()(   ffxxf . 所以,f (x) 在 0, 2      上的最大值和最小值分别为 2 1,1  . 10．（2013 年普通高等学校招生统一考试天津数学（理）试题（含答案））已知函数 2( ) 2 sin 2 6sin cos 2cos4 1,f x x x x x x           R . (Ⅰ) 求 f(x)的最小正周期; (Ⅱ) 求 f(x)在区间 0, 2      上的最大值和最小值. 11． （ 2013 年 普通 高 等学 校 招生 统 一考 试 辽宁 数 学（ 理） 试 题（ WORD 版 ））设向量    3sin ,sin , cos ,sinx , 0, .2a x x b x x        (I)若 .a b x 求 的值； (II)设函数    , .f x a b f x  求 的最大值 12．（2013 年高考上海卷（理））(6 分+8 分)已知函数 ( ) 2sin( )f x x ,其中常数 0  ; (1)若 ( )y f x 在 2[ , ]4 3   上单调递增,求 的取值范围; (2)令 2  ,将函数 ( )y f x 的图像向左平移 6  个单位,再向上平移 1 个单位,得到函数 ( )y g x 的图像,区间[ , ]a b ( ,a b R 且 a b )满足: ( )y g x 在[ , ]a b 上至少含有 30 个零 点,在所有满足上述条件的[ , ]a b 中,求b a 的最小值. (1)因为 0  ,根据题意有 34 2 02 4 3 2             (2) ( ) 2sin(2 )f x x , ( ) 2sin(2( )) 1 2sin(2 ) 16 3g x x x       1( ) 0 sin(2 )3 2 3g x x x k         或 7 ,12x k k Z    , 即 ( )g x 的零点相离间隔依次为 3  和 2 3  , 故若 ( )y g x 在[ , ]a b 上至少含有 30 个零点,则b a 的最小值为 2 4314 153 3 3       . 13．（2013 年普通高等学校招生统一考试安徽数学（理）试题（纯 WORD 版））已知函数 ( ) 4cos sin ( 0)4f x x x          的最小正周期为 . (Ⅰ)求 的值; (Ⅱ)讨论 ( )f x 在区间 0,2 上的单调性. 解 : (Ⅰ) 2)42sin(2)12cos2(sin2)cos(sincos22   xxxxxx 12 2    .所以 1,2)42sin(2)(  xxf (Ⅱ) ；解得，令时，当 8242]4,4[)42(]2,0[   xxxx 所以 .]28[]8,0[)( 上单调递减，上单调递增；在在 xfy  14．（2013 年普通高等学校招生统一考试福建数学（理）试题（纯 WORD 版））已知函数 的周期为 ,图像的一个对称中心为 ,将函数 图像上的所有点的横坐标伸长为原来的 2 倍(纵坐标不变),在将所得图像向右平移 个单位长度后得到函数 的图像. (1)求函数 与 的解析式; (2)是否存在 ,使得 按照某种顺序成等差数列?若存 在,请确定 的个数;若不存在,说明理由. (3)求实数 与正整数 ,使得 在 内恰有 2013 个零点. 解:(Ⅰ)由函数 的周期为 , ,得 又曲线 的一个对称中心为 , 故 ,得 ,所以 将函数 图象上所有点的横坐标伸长到原来的 倍(纵坐标不变)后可得 的图 象,再将 的图象向右平移 个单位长度后得到函数 (Ⅱ)当 时, , 所以 问题转化为方程 在 内是否有解 设 , 则 因为 ,所以 , 在 内单调递增 又 , 且函数 的图象连续不断,故可知函数 在 内存在唯一零点 , 即存在唯一的 满足题意 (Ⅲ)依题意, ,令 当 ,即 时, ,从而 不是方程 的解, 所以方程 等价于关于 的方程 , 现研究 时方程解的情况 令 , 则问题转化为研究直线 与曲线 在 的交点情况 ,令 ,得 或 当 变化时, 和 变化情况如下表 当 且 趋近于 时, 趋向于 当 且 趋近于 时, 趋向于 当 且 趋近于 时, 趋向于 当 且 趋近于 时, 趋向于 故当 时,直线 与曲线 在 内有无交点,在 内有 个交点; 当 时,直线 与曲线 在 内有 个交点,在 内无交点; 当 时,直线 与曲线 在 内有 个交点,在 内有 个交 点 由函数 的周期性,可知当 时,直线 与曲线 在 内总有偶数 个交点,从而不存在正整数 ,使得直线 与曲线 在 内恰有 个交 点;当 时,直线 与曲线 在 内有 个交点,由周期 性, ,所以 综上,当 , 时,函数 在 内恰有 个零点 15．（2013 年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯 WORD 版含附加题）） 本小题满分 14 分.已知 (cos ,sin ) (cos ,sin )a b    ＝ ， ,  0 . (1)若| | 2a b   ,求证: a b  ;(2)设 (0,1)c  ,若 a b c    ,求 , 的值. 解:(1)∵ 2||  ba ∴ 2|| 2  ba 即   22 222  bbaaba , 又 ∵ 1sincos|| 2222  aa , 1sincos|| 2222  bb ∴ 222  ba ∴ 0ba ∴ ba (2)∵ )1,0()sinsin,cos(cosba   ∴      1sinsin 0coscos   即        sin1sin coscos 两边分别平方再相加得: sin221  ∴ 2 1sin  ∴ 2 1sin  ∵  0 ∴  6 1,6 5  16．（2013 年普通高等学校招生统一考试广东省数学（理）卷（纯 WORD 版））已知函数 ( ) 2 cos 12f x x      , xR . (Ⅰ) 求 6f     的值; (Ⅱ) 若 3cos 5   , 3 ,22      ,求 2 3f     . (Ⅰ) 2 cos 2 cos 2 cos 16 6 12 4 4f                            ; (Ⅱ) 2 2 cos 2 2 cos 2 cos2 sin 23 3 12 4f                               因为 3cos 5   , 3 ,22      ,所以 4sin 5    , 所以 24sin 2 2sin cos 25      , 2 2 7cos2 cos sin 25       所以 2 3f     cos2 sin 2   7 24 17 25 25 25         . 17．（2013 年高考湖南卷（理））已知函数 2( ) sin( ) cos( ). ( ) 2sin6 3 2 xf x x x g x      . (I)若 是第一象限角,且 3 3( ) 5f   .求 ( )g  的值; (II)求使 ( ) ( )f x g x 成立的 x 的取值集合. 解: (I) 5 33sin3)(sin3sin2 3cos2 1cos2 1sin2 3)(  fxxxxxxf . 5 1cos12sin2)(,5 4cos)2,0(,5 3sin 2   g且 (II) 2 1)6sin(cos2 1sin2 3cos1sin3)()(  xxxxxxgxf Zkkkxkkx  ],3 22,2[]6 52,62[6  18．（2013 年上海市春季高考数学试卷(含答案)）本题共有 2 个小题,第一小题满分 4 分,第 二小题满分 9 分. 在平面直角坐标系 xOy 中,点 A 在 y 轴正半轴上,点 nP 在 x 轴上,其横坐标为 nx ,且{ }nx 是首项为 1、公比为 2 的等比数列,记 1n n nP AP   , n N  . (1)若 3 1arctan 3   ,求点 A 的坐标; (2)若点 A 的坐标为 (0 8 2)， ,求 n 的最大值及相应 n 的值. P20 x y A P1 P3 P4 [解](1) (2) [解](1)设 (0 )A t， ,根据题意, 12n nx  .由 3 1arctan 3   ,知 3 1tan 3   , 而 34 4 3 3 4 3 2 2 34 4 3 ( ) 4tan tan( ) 321 xx t x x tt tOAP OAP xx t x x t t t             , 所以 2 4 1 32 3 t t  ,解得 4t  或 8t  . 故点 A 的坐标为 (0 4)， 或 (0 8)， . (2)由题意,点 nP 的坐标为 1(2 0)n ， , 12tan 8 2 n nOAP    . 1 1 1 1 2 1 2 2 2 18 2 8 2tan tan( ) 2 2 2 16 2 21 8 2 8 2 8 2 8 2 2 8 2 n n n n n n n n n n n OAP OAP                  . 因为16 2 2 2 22 8 2 n n   ,所以 1 2tan 42 2n   , 当且仅当16 2 2 2 8 2 n n  ,即 4n  时等号成立. 易知 0 tan2n y x  ， 在 (0 )2 ， 上为增函数, 因此,当 4n  时, n 最大,其最大值为 2arctan 4 . 2012 年高考题 一、选择题 1.【2012 高考重庆理 5】设 tan ,tan  是方程 2 3 2 0x x   的两个根，则 tan( )  的 值为 （A）-3 （B）-1 （C）1 （D）3 【答案】A 【解析】因为  tan,tan 是方程 2 3 2 0x x   的两个根，所以 3tantan   ， 2tantan  ，所以 321 3 tantan1 tantan)tan(     ，选 A. 2.【2012 高考浙江理 4】把函数 y=cos2x+1 的图象上所有点的横坐标伸长到原来的 2 倍（纵 坐标不变），然后向左平移 1 个单位长度，再向下平移 1 个单位长度，得到的图像是 【答案】A 【解析】把函数 y＝cos2x＋1 的图像上所有点的横坐标伸长到原来的 2 倍(纵坐标不变) 得：y1＝cosx＋1，向左平移 1 个单位长度得：y2＝cos(x+1)＋1，再向下平移 1 个单位长度得： y3＝cos(x+1)．令 x＝0，得：y3＞0；x＝ 12  ，得：y3＝0；观察即得答案． 3.【2012 高考新课标理 9】已知 0  ，函数 ( ) sin( )4f x x   在 ( , )2   上单调递减.则 的取值范围是（ ） ( )A 1 5[ , ]2 4 ( )B 1 3[ , ]2 4 ( )C 1(0, ]2 ( )D (0,2] 【答案】A 【解析】法 1：函数 )4sin()(   xxf 的导数为 )4cos()('   xxf ，要使函数 )4sin()(   xxf 在 ),2(  上单调递减，则有 0)4cos()('   xxf 恒成立， 则  kxk 22 3 422  ， 即  kxk 24 524  ， 所 以 Zkkxk  ，         2 4 2 4 ，当 0k 时，     4 5 4  x ，又   x2 ，所以 有      4 5,24 ，解得 4 5,2 1   ，即 4 5 2 1   ，选 A. 法 2：选 A 5 92 ( ) [ , ]4 4 4x        不合题意 排除 ( )D 3 51 ( ) [ , ]4 4 4x        合题意 排除 ( )( )B C 另： ( ) 22        ， 3( ) [ , ] [ , ]4 2 4 4 2 2x             得： 3 1 5,2 4 2 4 2 2 4              4.【2012 高考四川理 4】如图，正方形 ABCD 的边长为1，延长 BA 至 E ，使 1AE  ，连 接 EC 、 ED 则sin CED  （ ） A、 3 10 10 B、 10 10 C、 5 10 D、 5 15 【答案】B 【解析】 2EB EA AB   ， 2 2 4 1 5EC EB BC     ， 3 4 2 4EDC EDA ADC           ， 由正弦定理得 sin 1 5 sin 55 CED DC EDC CE     ， 所以 5 5 3 10sin sin sin5 5 4 10CED EDC     g g . [点评]注意恒等式 sin2α+cos2α=1 的使用，需要用α的的范围决定其正余弦值的正负情况. 5.【2012 高考陕西理 9】在 ABC 中，角 , ,A B C 所对边长分别为 , ,a b c ，若 2 2 22a b c  ， 则 cosC 的最小值为（ ） A. 3 2 B. 2 2 C. 1 2 D. 1 2  【答案】C. 【解析】由余弦定理知 2 1 4 2 42 )(2 1 2cos 22 2222 222    ab ab ab ba ab baba ab cbaC ， 故选Ｃ． 6.【2012 高考山东理 7】若 4 2        ， ， 3 7sin 2 = 8  ，则sin  （A） 3 5 （B） 4 5 （C） 7 4 （D） 3 4 【答案】D 【 解 析 】 法 1 ： 因 为 ]2,4[   ， 所 以 ],2[2   ， 02cos  ， 所 以 8 12sin12cos 2   ， 又 8 1sin212cos 2   ， 所 以 16 9sin 2  ， 4 3sin  ，选 D. 法 2：由 4 2        ， 及 3 7sin 2 = 8  可得 4 3 4 7 16 7769 16 7616 8 7312sin1cossin   ， 而当 4 2        ， 时  cossin  ，结合选项即可得 4 7cos,4 3sin   .答案应选 D。 7.【2012 高考辽宁理 7】已知sin cos 2   ， (0，π)，则 tan = (A) 1 (B) 2 2  (C) 2 2 (D) 1 【答案】A 【解析一】 sin cos 2, 2 sin( ) 2, sin( ) 14 4             3(0 ), , tan 14          ， ，故选 A 【解析二】 2sin cos 2, (sin cos ) 2, sin 2 1,            3 3(0, ), 2 (0,2 ), 2 , , tan 12 4                  ，故选 A 【点评】本题主要考查三角函数中的和差公式、倍角公式、三角函数的性质以及转化思想和 运算求解能力，难度适中。 8.【2012 高考江西理 4】若 tan + 1 tan =4,则 sin2 = A． 1 5 B. 1 4 C. 1 3 D. 1 2 【答案】D 【命题立意】本题考查三角函数的倍角公式以及同角的三角函数的基本关系式。 【解析】由 4tan 1tan   得， 4cossin cossin sin cos cos sin 22        ，即 4 2sin2 1 1   ， 所以 2 12sin  ，选 D. 【点评】本题需求解正弦值，显然必须切化弦，因此需利用公式 sintan cos   转化；另外， 2 2sin cos  在转化过程中常与“1”互相代换，从而达到化简的目的；关于正弦、余弦 的齐次分式，常将正弦、余弦转化为正切，即弦化切，达到求解正切值的目的. 体现考纲中 要求理解三角函数的基本关系式，二倍角公式.来年需要注意二倍角公式的正用，逆用等. 9.【2012 高考湖南理 6】函数 f（x）=sinx-cos(x+ 6  )的值域为 A． [ -2 ,2] B.[- 3 , 3 ] C.[-1,1 ] D.[- 3 2 , 3 2 ] 【答案】B 【解析】f（x）=sinx-cos(x+ 6  ) 3 1sin cos sin 3sin( )2 2 6x x x x      ，  sin( ) 1,16x    ， ( )f x 值域为[- 3 , 3 ]. 【点评】利用三角恒等变换把 ( )f x 化成 sin( )A x  的形式，利用  sin( ) 1,1x    ， 求得 ( )f x 的值域. 10.【2012 高考上海理 16】在 ABC 中，若 CBA 222 sinsinsin  ，则 ABC 的形状是 （ ） A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定 【答案】C 【解析】根据正弦定理可知由 CBA 222 sinsinsin  ,可知 222 cba  ，在三角形中 02cos 222  ab cbaC ，所以C 为钝角，三角形为钝角三角形，选 C. 【点评】本题主要考查正弦定理及其推理、余弦定理的运用.主要抓住所给式子的结构来选 择定理，如果出现了角度的正弦值就选择正弦定理，如果出现角度的余弦值就选择余弦定理. 本题属于中档题. 11.【2012 高考天津理 2】设 ,R 则“ 0 ”是“ ))(cos()( Rxxxf   为偶函数” 的 （A）充分而不必要条件 （B）必要而不充分条件 （C）充分必要条件 （D）既不充分与不必要条件 【答案】A 【命题意图】本试题主要考查了三角函数的奇偶性的判定以及充分条件与必要条件的判定. 【解析】函数 )cos()(  xxf 若为偶函数，则有 Zkk  , ,所以“ 0 ”是 “ )cos()(  xxf 为偶函数”的充分不必要条件，选 A. 12.【2012 高考天津理 6】在 ABC 中，内角 A，B，C 所对的边分别是 cba ,, ，已知 8b=5c， C=2B，则 cosC= （A） 25 7 （B） 25 7 （C） 25 7 （D） 25 24 【答案】A 【命题意图】本试题主要考查了正弦定理、三角函数中的二倍角公式. 考查学生分析、转化 与计算等能力. 【 解 析 】 因 为 BC 2 , 所 以 BBBC cossin2)2sin(sin  , 根 据 正 弦 定 理 有 B b C c sinsin  ， 所 以 5 8 sin sin  B C b c ， 所 以 5 4 5 8 2 1 sin2 sincos  B CB 。 又 1cos2)2cos(cos 2  BBC ，所以 25 7125 1621cos2cos 2  BC ，选 A. 13.【2012 高考全国卷理 7】已知α为第二象限角， 3 3cossin   ，则 cos2α= (A) 5- 3 （B） 5- 9 (C) 5 9 (D) 5 3 【答案】A 【命题意图】本试题主要考查了三角函数中两角和差的公式以及二倍角公式的运用。首先利 用平方法得到二倍角的正弦值，然后然后利用二倍角的余弦公式，将所求的转化为单角的正 弦值和余弦值的问题。 【 解 析 】 因 为 3 3cossin   所 以 两 边 平 方 得 3 1cossin21   ， 所 以 03 2cossin2  ， 因 为 已 知 α 为 第 二 象 限 角 ， 所 以 0cos,0sin   ， 3 15 3 5 3 21cossin21cossin   ， 所 以 )sin)(cossin(cossincos2cos 22   = 3 5 3 3 3 15  ，选 A. 二、填空题 14.【2012 高考湖南理 15】函数 f（x）=sin ( x  )的导函数 ( )y f x 的部分图像如图 4 所示，其中，P 为图像与 y 轴的交点，A,C 为图像与 x 轴的两个交点，B 为图像的最低点. （1）若 6   ，点 P 的坐标为（0， 3 3 2 ），则  ; （2）若在曲线段 ABC 与 x 轴所围成的区域内随机取一点，则该点在△ABC 内的概率 为 . 【答案】（1）3；（2） 4  【解析】（1） ( )y f x cos( )x    ，当 6   ，点 P 的坐标为（0， 3 3 2 ）时 3 3cos , 36 2     ； （2）由图知 2 2 2 TAC      ， 1 2 2ABCS AC    ，设 ,A B 的横坐标分别为 ,a b . 设 曲 线 段 ABC 与 x 轴 所 围 成 的 区 域 的 面 积 为 S 则 ( ) ( ) sin( ) sin( ) 2 b b aa S f x dx f x a b          ，由几何概型知该点在△ABC 内的概率为 2 2 4 ABCSP S     . 【点评】本题考查三角函数的图像与性质、几何概型等，（1）利用点 P 在图像上求 ， （2）几何概型，求出三角形面积及曲边形面积，代入公式即得. 15.【2012 高考湖北理 11】设△ ABC 的内角 A ， B ， C 所对的边分别为 a ， b ， c . 若 ( )( )a b c a b c ab     ，则角C  ． 【答案】 3 2 考点分析：考察余弦定理的运用. 【解析】 2 2 2 2 2 2 a =-a -ab 1 2cos = ,2 2 2 3 a b c b a b cC Cab ab          由（ +b-c）(a+b-c)=ab,得到 根据余弦定理 故 16.【2012 高考北京理 11】在△ABC 中，若 a =2，b+c=7，cosB= 4 1 ，则 b=_______。 【答案】4 【解析】在△ABC 中，利用余弦定理 c bcbc ac bcaB 4 ))((4 4 1 2cos 222  c bc 4 )(74  ，化简得： 0478  bc ，与题目条件 7 cb 联立，可解得       2 4 3 a b c . 17.【2012 高考安徽理 15】设 ABC 的内角 , ,A B C 所对的边为 , ,a b c ；则下列命题正确的 是 _____ ①若 2ab c ；则 3C  ②若 2a b c  ；则 3C  ③若 3 3 3a b c  ；则 2C  ④若 ( ) 2a b c ab  ；则 2C  ⑤若 2 2 2 2 2( ) 2a b c a b  ；则 3C  【答案】①②③ 【命题立意】本题解三角形的知识，主要涉及余弦定理与基本不等式的运算。 【解析】正确的是 _____ ① 2 2 2 2 2 1cos 2 2 2 3 a b c ab abab c C Cab ab          ② 2 2 2 2 2 24( ) ( ) 12 cos 2 8 2 3 a b c a b a ba b c C Cab ab             ③当 2C  时， 2 2 2 3 2 2 3 3c a b c a c b c a b       与 3 3 3a b c  矛盾 ④取 2, 1a b c   满足 ( ) 2a b c ab  得： 2C  ⑤取 2, 1a b c   满足 2 2 2 2 2( ) 2a b c a b  得： 3C  18.【2012 高考福建理 13】已知△ABC 得三边长成公比为 2 的等比数列，则其最大角的余 弦值为_________. 【答案】 4 2 ． 【命题立意】本题考查了解三角形和等比数列的相关知识，难度适中． 【解析】设最小边长为 a ，则另两边为 aa 2,2 . 所以最大角余弦 4 2 22 42cos 222    aa aaa 19.【2012 高考重庆理 13】设 ABC 的内角 , ,A B C 的对边分别为 , ,a b c ，且 5 3cos A ， 13 5cos B , 3b 则 c  【答案】 5 14 【 解 析 】 因 为 5 3cos A , 13 5cos B , 所 以 5 4sin A ， 13 12sin B ， 65 56 5 3 13 12 13 5 5 4)sin(sin  BAC ,根据正弦定理 C c B b sinsin  得 65 56 13 12 3 c ,解 得 5 14c . 20.【2012 高考上海理 4】若 )1,2(n 是直线l 的一个法向量，则l 的倾斜角的大小 为 （结果用反三角函数值表示）。 【答案】 2arctan 【解析】设倾斜角为 ，由题意可知，直线的一个方向向量为（1,2），则 2tan  ， ∴ = 2arctan 。 【点评】本题主要考查直线的方向向量、直线的倾斜角与斜率的关系、反三角函数的表示. 直线的倾斜角的取值情况一定要注意，属于低档题，难度较小. 21. 【 2012 高 考 全 国 卷 理 14 】 当 函 数 取 得 最 大 值 时 ， x=___________. 【答案】 6 5x 【命题意图】本试题主要考查了三角函数性质的运用，求解值 域的问题。首先化为单一三 角函数，然后利用定义域求解角的范围，从而结合三角函数图像得到最值点。 【 解 析 】 函 数 为 )3sin(2cos3sin  xxxy ， 当 20  x 时 ， 3 5 33   x ，由三角函数图象可知，当 23  x ，即 6 5x 时取得最大值，所 以 6 5x . 22.【2012 高考江苏 11】（5 分）设 为锐角，若 4cos 6 5       ，则 )122sin( a 的值为 ▲ ． 【答案】 17 250 。 【考点】同角三角函数，倍角三角函数，和角三角函数。 【解析】∵ 为锐角，即 0 2< <  ，∴ 2=6 6 2 6 3< <       。 ∵ 4cos 6 5       ，∴ 3sin 6 5       。∴ 3 4 24sin 2 2sin cos =2 =3 6 6 5 5 25                          。 ∴ 7cos 2 3 25       。 ∴ sin(2 )=sin(2 )=sin 2 cos cos 2 sin12 3 4 3 4 3 4a a a a                     24 2 7 2 17= = 225 2 25 2 50   。 三、解答题 23.【2012 高考新课标理 17】（本小题满分 12 分） 已知 , ,a b c 分别为 ABC 三个内角 , ,A B C 的对边， cos 3 sin 0a C a C b c    （1）求 A （2）若 2a  ， ABC 的面积为 3 ；求 ,b c . 【答案】（1）由正弦定理得： cos 3 sin 0 sin cos 3sin sin sin sina C a C b c A C A C B C        sin cos 3sin sin sin( ) sin 13sin cos 1 sin( 30 ) 2 30 30 60 A C A C a C C A A A A A                     （2） 1 sin 3 42S bc A bc    2 2 2 2 cos 4a b c bc A b c      24.【2012 高考湖北理 17】（本小题满分 12 分） 已 知 向 量 (cos sin , sin )x x x   a ， ( cos sin , 2 3cos )x x x    b ， 设 函 数 ( )f x   a b ( )xR 的图象关于直线 πx  对称，其中 ，  为常数，且 1( , 1)2   . （Ⅰ）求函数 ( )f x 的最小正周期； （Ⅱ）若 ( )y f x 的图象经过点 π( ,0)4 ，求函数 ( )f x 在区间 3π[0, ]5 上的取值范围. 【答案】（Ⅰ）因为 2 2( ) sin cos 2 3sin cosf x x x x x         cos2 3sin 2x x      π2sin(2 )6x    . 由直线 πx  是 ( )y f x 图象的一条对称轴，可得 πsin(2 π ) 16     ， 所以 π π2 π π ( )6 2k k     Z ，即 1 ( )2 3 k k    Z ． 又 1( , 1)2   ， k Z ，所以 1k  ，故 5 6   . 所以 ( )f x 的最小正周期是 6π 5 . （Ⅱ）由 ( )y f x 的图象过点 π( ,0)4 ，得 π( ) 04f  ， 即 5 π π π2sin( ) 2sin 26 2 6 4          ，即 2   . 故 5 π( ) 2sin( ) 23 6f x x   ， 由 3π0 5x  ，有 π 5 π 5π 6 3 6 6x    ， 所以 1 5 πsin( ) 12 3 6x    ，得 5 π1 2 2sin( ) 2 2 23 6x       ， 故函数 ( )f x 在 3π[0, ]5 上的取值范围为[ 1 2, 2 2]   . 25.【2012 高考安徽理 16】）(本小题满分 12 分) 设函数 22( ) cos(2 ) sin2 4f x x x   。 （I）求函数 ( )f x 的最小正周期； （ II ） 设 函 数 ( )g x 对 任 意 x R ， 有 ( ) ( )2g x g x  ， 且 当 [0, ]2x  时 ， 1( ) ( )2g x f x  ，求函数 ( )g x 在[ ,0] 上的解析式。 【答案】本题考查两角和与差的三角函数公式、二倍角公式、三角函数的周期等性质、分段 函数解析式等基础知识，考查分类讨论思想和运算求解能力。 【解析】 22 1 1 1( ) cos(2 ) sin cos2 sin 2 (1 cos2 )2 4 2 2 2f x x x x x x       1 1 sin 22 2 x  ， （I）函数 ( )f x 的最小正周期 2 2T    （2）当 [0, ]2x  时， 1 1( ) ( ) sin 22 2g x f x x   当 [ ,0]2x   时， ( ) [0, ]2 2x    1 1( ) ( ) sin 2( ) sin 22 2 2 2g x g x x x       当 [ , )2x    时， ( ) [0, )2x   1 1( ) ( ) sin 2( ) sin 22 2g x g x x x      得函数 ( )g x 在[ ,0] 上的解析式为 1 sin 2 ( 0)2 2( ) 1 sin 2 ( )2 2 x x g x x x            。 26.【2012 高考四川理 18】(本小题满分 12 分) 函数 2( ) 6cos 3 cos 3( 0)2 xf x x      在一个周期内的图象如图所示， A 为图 象的最高点， B 、C 为图象与 x 轴的交点，且 ABC 为正三角形。 （Ⅰ）求 的值及函数 ( )f x 的值域； （Ⅱ）若 0 8 3( ) 5f x  ，且 0 10 2( , )3 3x   ，求 0( 1)f x  的值。 【答案】本题主要考查三角函数的图像与性质、同角三角函数的关系、两角和差公式，倍角 公式等基础知识，考查基本运算能力，以及数形结合思想，化归与转化思想. [解析]（Ⅰ）由已知可得： 2( ) 6cos 3 cos 3( 0)2 xf x x      =3cosωx+ )3sin(32sin3   xx 又由于正三角形 ABC 的高为 2 3 ，则 BC=4 所以，函数 482824)(    ，得，即的周期Txf 所以，函数 ]32,32[)( 的值域为xf 。……………………6 分 （Ⅱ）因为 ，由 5 38)( 0 xf （Ⅰ）有 ， 5 38)34(sin32)( 0 0  xxf 5 4)34(sin 0  x即 由 x0 )2,2()34 x(3 2 3 10 0   ），得，（ 所以， 5 3)5 4(1)34(cos 20  x即 故  )1( 0xf  )344(sin32 0 x ]4)34(sin[32 0  x )2 2 5 3 2 2 5 4(32 4sin)34cos(4cos)34([sin32 00    xx 5 67 ………………………………………………………12 分 27.【2012 高考陕西理 16】（本小题满分 12 分） 函数 ( ) sin( ) 16f x A x    （ 0, 0A   ）的最大值为 3， 其图像相邻两条对称轴之 间的距离为 2  ， （1）求函数 ( )f x 的解析式； （2）设 (0, )2   ，则 ( ) 22f   ，求 的值。 【解析】（Ⅰ）∵函数  f x 的最大值是 3，∴ 1 3A  ，即 2A  。 ∵函数图像的相邻两条对称轴之间的距离为 2  ，∴最小正周期T  ，∴ 2  。 故函数  f x 的解析式为 ( ) 2sin(2 ) 16f x x    。 （Ⅱ）∵ ( )2f  2sin( ) 1 26     ，即 1sin( )6 2    ， ∵ 0 2   ，∴ 6 6 3       ，∴ 6 6     ，故 3   。 28.【2012 高考广东理 16】（本小题满分 12 分） 已知函数 )6cos(2)(   xxf ，（其中ω＞0，x∈R）的最小正周期为 10π． （1）求ω的值； （2）设 ]2,0[,   ， 5 6)3 55(  f ， 17 16)6 55(  f ，求 cos（α＋β）的值． 【答案】本题考查三角函数求值，三角恒等变换，利用诱导公式化简三角函数式与两角和的 余弦公式求值，难度较低。 【解析】（1） 2 110 5T       （2） 5 6 3 3 4(5 ) cos( ) sin ,cos3 5 2 5 5 5f               5 16 8 15(5 ) cos ,sin6 17 17 17f        4 8 3 15 13cos( ) cos cos sin sin 5 17 5 17 85               29.【2012 高考山东理 17】（本小题满分 12 分） 已知向量 (sin ,1), ( 3 cos , cos2 )( 0)3 Am x n A x x A    ，函数 ( )f x m n   的最大值 为 6. （Ⅰ）求 A ； （Ⅱ）将函数 ( )y f x 的图象向左平移 12  个单位，再将所得图象上各点的横坐标缩短为原 来的 1 2 倍，纵坐标不变，得到函数 ( )y g x 的图象.求 ( )g x 在 5[0, ]24  上的值域. 解：（Ⅰ） ( )  f x m n 3 sin cos cos22 3 1( sin 2 cos2 )2 2 sin(2 ) AA x x x A x x A x         因为 0A  ， 由题意知 6A  ． （Ⅱ）由（I） ( ) 6sin(2 )f x x    将 ( )y f x 的图象向左平移   个单位后得到 6sin[2( ) ] 6sin(2 )y x x         的图象； 再将得到图象上各点横坐标缩短为原来的 1 2 倍，纵坐标不变，得到 6sin(4 )y x    的图象． 因此 ( ) 6sin(4 )g x x    ， 因为 5[0 , ]x   ， 所以 74 [ , ]x       ， 所以 1sin(4 ) [ ,1]2x    ， 所以 ( )g x 在 5[0 , ]  上的值域为[ 3 , 6] ． 30.【2012 高考北京理 15】（本小题共 13 分）已知函数 x xxxxf sin 2sin)cos(sin)(  。 （1）求 )(xf 的定义域及最小正周期； （2）求 )(xf 的单调递减区间。 解（1）：sin 0 ( )x x k k Z    得：函数 ( )f x 的定义域为{ , }x x k k Z  (sin cos )sin 2( ) (sin cos ) 2cossin x x xf x x x xx     sin 2 (1 cos2 ) 2 sin(2 ) 14x x x       得： )(xf 的最小正周期为 2 2T    ； （2）函数 siny x 的单调递增区间为[2 ,2 ]( )2 2k k k Z     则 32 2 22 4 2 8 8k x k k x k                 得： )(xf 的单调递增区间为 3[ , ),( , ]( )8 8k k k k k Z       31.【2012 高考重庆理 18】（本小题满分 13 分（Ⅰ）小问 8 分（Ⅱ）小问 5 分） 设 )2cos(sin)6cos(4)( xxxxxf   ，其中 .0 （Ⅰ）求函数 )(xfy  的值域 （Ⅱ）若 )(xfy  在区间     2,2 3 x 上为增函数，求  的最大值. 解：（1）   3 14 cos sin sin cos22 2f x x x x x          2 2 22 3sin cos 2sin cos sinx x x x x        3sin 2 1x  因 1 sin 2 1x   ，所以函数  y f x 的值域为 1 3,1 3    （ 2 ） 因 siny x 在 每 个 闭 区 间  2 ,22 2k k k Z        上 为 增 函 数 ， 故   3sin 2 1f x x   0  在每个闭区间  ,4 4 k k k Z              上为增函数。 依题意知 3 ,2 2       ,4 4 k k             对某个 k Z 成立，此时必有 0k  ，于是 3 2 4 2 4            ，解得 1 6   ，故 的最大值为 1 6 。 32.【2012 高考浙江理 18】(本小题满分 14 分)在  ABC 中，内角 A，B，C 的对边分别 为 a，b，c．已知 cosA＝ 2 3 ，sinB＝ 5 cosC． (Ⅰ)求 tanC 的值； (Ⅱ)若 a＝ 2 ，求  ABC 的面积． 【答案】本题主要考查三角恒等变换，正弦定理，余弦定理及三角形面积求法等知识点。 (Ⅰ)∵cosA＝ 2 3 ＞0，∴sinA＝ 2 51 cos 3A  ， 又 5 cosC＝sinB＝sin(A＋C)＝sinAcosC＋sinCcosA ＝ 5 3 cosC＋ 2 3 sinC． 整理得：tanC＝ 5 ． (Ⅱ)由图辅助三角形知：sinC＝ 5 6 ． 又由正弦定理知： sin sin a c A C  ， 故 3c  ． (1) 对角 A 运用余弦定理：cosA＝ 2 2 2 2 2 3 b c a bc    ． (2) 解(1) (2)得： 3b  or b＝ 3 3 (舍去)． ∴  ABC 的面积为：S＝ 5 2 ． 33.【2012 高考辽宁理 17】(本小题满分 12 分) 在 ABC 中，角 A、B、C 的对边分别为 a，b，c。角 A，B，C 成等差数列。 (Ⅰ)求 cos B 的值； (Ⅱ)边 a，b，c 成等比数列，求sin sinA C 的值。 【命题意图】本题主要考查等差数列、等比数列概念、正余弦定理应用，是容易题. 【解析】（1）由已知 12 = + , + + = , = ,cos =3 2B A C A B C B B  ……6 分 （2）解法一： 2 =b ac ，由正弦定理得 2 3sin sin =sin = 4A C B 解法二： 2 =b ac ， 2 2 2 2 21 + - + -=cos = =2 2 2 a c b a c acB ac ac ，由此得 2 2+ - = ,a c ac ac 得 =a c 所以 = = = 3A B C  ， 3sin sin = 4A C …… 12 分 【点评】本题主要考查三角形的正弦定理、余弦定理、三角形内角和定理及等差、等比数列 的定义，考查转化思想和运算求解能力，属于容易题。第二小题既可以利用正弦定理把边的 关系转化为角的关系，也可以利用余弦定理得到边之间的关系，再来求最后的结果。 34.【2012 高考江西理 17】（本小题满分 12 分） 在△ABC 中，角 A,B,C 的对边分别为 a，b，c。已知 , sin( ) sin( )4 4 4A b C c B a       （1）求证： 2B C   （2）若 2a  ，求△ABC 的面积。 解：（1）证明：由 sin( ) sin( )4 4b C c B a     及正弦定理得： sin sin( ) sin sin( ) sin4 4B C C B A     ， 即 2 2 2 2 2sin ( sin sin ) sin ( sin sin )2 2 2 2 2B C C C B B    整理得：sin cos cos sin 1B C B C  ，所以sin( ) 1B C  ，又 30 , 4B C   所以 2B C   （2） 由（1）及 3 4B C   可得 5 ,8 8B C   ，又 , 24A a  所以 sin 5 sin2sin , 2sinsin 8 sin 8 a B a Cb cA A      ， 所以三角形 ABC 的面积 1 5 2 1sin 2 sin sin 2 sin cos sin2 8 8 8 8 2 4 2bc A          【点评】本题考查解三角形，三角形的面积，三角恒等变换、三角和差公式以及正弦定理的 应用.高考中，三角解答题一般有两种题型：一、解三角形：主要是运用正余弦定理来求解 边长，角度，周长，面积等；二、三角函数的图像与性质：主要是运用和角公式，倍角公式， 辅助角公式进行三角恒等变换，求解三角函数的最小正周期，单调区间，最值（值域）等. 来年需要注意第二种题型的考查. 35.【2012 高考全国卷理 17】（本小题满分 10 分） 三角形 ABC 的内角 A、B、C 的对边分别为 a、b、c，已知 cos（A-C）＋cosB=1，a=2c， 求 c. 【命题意图】本试题主要考查了解三角形的运用，给出两个公式，一个是边的关系，一个角 的关系，而求解的为角，因此要找到角的关系式为好。 【解析】由 ( )A B C B A C        ， 由正弦定理及 2a c 可得sin 2sinA C 所以 cos( ) cos cos( ) cos( ( )) cos( ) cos( )A C B A C A C A C A C           cos cos sin sin cos cos sin sin 2sin sinA C A C A C A C A C     故由 cos( ) cos 1A C B   与sin 2sinA C 可得 22sin sin 1 4sin 1A C C   而C 为三角形的内角且 2a c c  ，故 0 2C   ，所以 1sin 2C  ，故 6C  。 【点评】该试题从整体来看保持了往年的解题风格，依然是通过边角的转换，结合了三角形 的内角和定理的知识，以及正弦定理和余弦定理，求解三角形中的角的问题。试题整体上比 较稳定，思路也比较容易想，先将三角函数关系式化简后，得到 ,A C 角关系，然后结合 2a c ，得到两角的二元一次方程组，自然很容易得到角C 的值。 36.【2012 高考天津理 15】（本小题满分 13 分） 已知函数 .,1cos2)32sin()32sin()( 2 Rxxxxxf   （Ⅰ）求函数 )(xf 的最小正周期； （Ⅱ）求函数 )(xf 在区间 ]4,4[  上的最大值和最小值. 【 解 析 】 （ 1 ） 2( )=sin (2 + )+sin(2 )+2cos 13 3f x x x x   2sin 2 cos cos2 2 sin(2 )3 4x x x     函数 ( )f x 的最小正周期为 2 2T    （2） 3 22 sin(2 ) 1 1 ( ) 24 4 4 4 4 2 4x x x f x                      当 2 ( )4 2 8x x     时 ， ( ) 2maxf x  ， 当 2 ( )4 4 4x x       时 ， min( ) 1f x   【点评】该试题关键在于将已知的函数表达式化为 = sin ( + )y A x  的数学模型，再根据此 三角模型的图像与性质进行解题即可. 37.【2012 高考江苏 15】（14 分）在 ABC 中，已知 3AB AC BA BC      ． （1）求证： tan 3tanB A ； （2）若 5cos 5C  ，求 A 的值． 【 答 案 】 解 ： （ 1 ） ∵ 3AB AC BA BC      ， ∴ cos =3 cosAB AC A BA BC B    ， 即 cos =3 cosAC A BC B  。 由正弦定理，得 =sin sin AC BC B A ，∴sin cos =3sin cosB A A B  。 又 ∵ 0 < A B < ， ∴ cos 0 cos 0A> B >， 。 ∴ sin sin=3cos cos B A B A 即 tan 3tanB A 。 （2）∵ 5cos 05C ，∴ tan =1A 。∴ = 4A  。 【考点】平面微量的数量积，三角函数的基本关系式，两角和的正切公式，解三角形。 【解析】（1）先将 3AB AC BA BC      表示成数量积，再根据正弦定理和同角三角函数关 系式证明。 （2）由 5cos 5C  ，可求 tanC ，由三角形三角关系，得到  tan A B     ，从 而根据两角和的正切公式和（1）的结论即可求得 A 的值。 2011 年高考题 一、选择题 1.（山东理 6）若函数 ( ) sinf x x (ω>0)在区间 0, 3      上单调递增，在区间 ,3 2       上单 调递减，则ω= A．3 B．2 C． 3 2 D． 2 3 【答案】C 2.（山东理 9）函数 2sin2 xy x  的图象大致是 【答案】C 3.（全国大纲理 5）设函数 ( ) cos ( 0)f x x  ＞ ，将 ( )y f x 的图像向右平移 3  个单位长 度后，所得的图像与原图像重合，则 的最小值等于 A． 1 3 B．3 C． 6 D．9 【答案】C 4.（湖北理 3）已知函数 ( ) 3sin cos ,f x x x x R   ，若 ( ) 1f x  ，则 x 的取值范围为 A． | ,3x k x k k Z          B． | 2 2 ,3x k x k k Z          C． 5{ | , }6 6x k x k k Z       D． 5{ | 2 2 , }6 6x k x k k Z       【答案】B 5.（全国新课标理 11）设函数 ( ) sin( ) cos( )f x x x       ( 0,| | )2    的最小正 周期为 ，且 ( ) ( )f x f x  则 （A） ( )y f x 在 (0, )2  单调递减 （B） ( )y f x 在 3( , )4 4   单调递减 （C） ( )y f x 在 (0, )2  单调递增 （D） ( )y f x 在 3( , )4 4   单调递增 【答案】A 6.（安徽理 9）已知函数 ( ) sin(2 )f x x   ，其中 为实数，若 ( ) ( )6f x f  对 x R 恒 成立，且 ( ) ( )2f f  ，则 ( )f x 的单调递增区间是 （A） , ( )3 6k k k Z        （B） , ( )2k k k Z      （C） 2, ( )6 3k k k Z        （D） , ( )2k k k Z      【答案】C 二、填空题 7.（上海理 8）函数 sin( )cos( )2 6y x x    的最大值为 。 【答案】 2 3 4  8.（辽宁理 16）已知函数 )(xf =Atan（ x+ ）（ 2||,0   ）， y= )(xf 的部分图像如下图，则 )24( f ． 【答案】 3 三、解答题 9.（江苏 9）函数  ,,(),sin()( wAwxAxf  是常数， )0,0  wA 的部分图象如图所 示，则 f(0)= 【答案】 2 6 10（北京理 15） 已知函数 ( ) 4cos sin( ) 16f x x x    。 （Ⅰ）求 ( )f x 的最小正周期： （Ⅱ）求 ( )f x 在区间 ,6 4      上的最大值和最小值。 解：（Ⅰ）因为 1)6sin(cos4)(  xxxf 1)cos2 1sin2 3(cos4  xxx 1cos22sin3 2  xx xx 2cos2sin3  )62sin(2  x 所以 )(xf 的最小正周期为 （Ⅱ）因为 .3 2 626,46   xx 所以 于是，当 6,262   xx 即 时， )(xf 取得最大值 2； 当 )(,6,662 xfxx 时即   取得最小值—1. 11．（福建理 16） 已知等比数列{an}的公比 q=3，前 3 项和 S3= 13 3 。 （I）求数列{an}的通项公式； （II）若函数 ( ) sin(2 )( 0,0 )f x A x A p        在 6x  处取得最大值，且最大值 为 a3，求函数 f（x）的解析式。 本小题主要考查等比数列、三角函数等基础知识，考查运算求解能力，考查函数与方程思想， 满分 13 分。 解：（I）由 3 1 3 (1 3 )13 133, ,3 1 3 3 aq S    得 解得 1 1.3a  所以 1 21 3 3 .3 n n na     （II）由（I）可知 2 33 , 3.n na a 所以 因为函数 ( )f x 的最大值为 3，所以 A=3。 因为当 6x  时 ( )f x 取得最大值， 所以 sin(2 ) 1.6     又 0 , .6     故 所以函数 ( )f x 的解析式为 ( ) 3sin(2 )6f x x   12.（广东理 16） 已知函数 1( ) 2sin( ), .3 6f x x x R   （1）求 5( )4f  的值； （2）设 10 6, 0, , (3 ) , (3 2 ) ,2 2 13 5f a f            求 cos( )  的值． 解：（1） 5 1 5( ) 2sin( )4 3 4 6f     2sin 24    ； （2） 10 13 2sin 3 2sin ,13 2 3 2 6f                         6 1(3 2 ) 2sin (3 2 ) 2sin 2cos ,5 3 6 2f                         5 3sin ,cos ,13 5     2 2 5 12cos 1 sin 1 ,13 13            2 2 3 4sin 1 cos 1 ,5 5           故 3 12 5 4 56cos( ) cos cos sin sin .5 13 13 5 65              13.（湖北理 16） 设 ABC 的内角 A、B、C、所对的边分别为 a、b、c，已知 11. 2.cos .4a b C   （Ⅰ）求 ABC 的周长 （Ⅱ）求  cos A C 的值 本小题主要考查三角函数的基本公式和解斜三角形的基础知识，同时考查基本运算能力。（满 分 10 分） 解：（Ⅰ） 2 2 2 12 cos 1 4 4 44c a b ab C        2.c  ABC 的周长为 1 2 2 5.a b c      （Ⅱ） 2 21 1 15cos , sin 1 cos 1 ( ) .4 4 4C C C       15 sin 154sin 2 8 a CA c     ,a c A C   ，故 A 为锐角， 2 215 7cos 1 sin 1 ( ) .8 8A A      7 1 15 15 11cos( ) cos cos sin sin .8 4 8 8 16A C A C A C         14.（四川理 17） 已知函数 7 3( ) sin( ) cos( ),4 4f x x x x R      （1）求 ( )f x 的最小正周期和最小值； （2）已知 4 4cos( ) ,cos( ) ,(0 )5 5 2a             ，求证： 2[ ( )] 2 0f    解析： 7 7 3 3( ) sin cos cos sin cos cos sin sin4 4 4 4 2 sin 2 cos 2sin( )4 f x x x x x x x x              max2 , ( ) 2T f x   （2） 4cos( ) cos cos sin sin (1)5 4cos( ) cos cos sin sin (2)5 cos cos 0 0 cos 02 2                                        2( ) 2 ( ( )) 2 0f f      15.（天津理 15） 已知函数 ( ) tan(2 ),4f x x   （Ⅰ）求 ( )f x 的定义域与最小正周期； （II）设 0, 4      ，若 ( ) 2cos2 ,2f   求 的大小． 本小题主要考查两角和的正弦、余弦、正切公式，同角三角函数的基本关系，二倍角的正弦、 余弦公式，正切函数的性质等基础知识，考查基本运算能力.满分 13 分. （I）解：由 2 ,4 2x k k Z      ， 得 ,8 2 kx k Z    . 所以 ( )f x 的定义域为 { | , }8 2 kx R x k Z     ( )f x 的最小正周期为 .2  （II）解：由 ( ) 2cos2 ,2 af a 得 tan( ) 2cos2 ,4a a  2 2 sin( )4 2(cos sin ), cos( )4 a a a a       整理得 sin cos 2(cos sin )(cos sin ).cos sin a a a a a aa a     因为 (0, )4a  ，所以 sin cos 0.a a  因此 2 1 1(cos sin ) , sin 2 .2 2a a a  即 由 (0, )4a  ，得 2 (0, )2a  . 所以 2 , .6 12a a  即 16.（重庆理 16） 设 a R ，     2cos sin cos cos 2f x x a x x x       满足  03f f     ，求函数 ( )f x 在 11[ , ]4 24   上的最大值和最小值. 解： 2 2( ) sin cos cos sinf x a x x x x   sin 2 cos2 .2 a x x  由 3 1( ) (0) 1, 2 3.3 2 2 2 af f a       得 解得 因此 ( ) 3sin 2 cos2 2sin(2 ).6f x x x x     当 [ , ] ,2 [ , ], ( )4 3 6 3 2x x f x      时 为增函数， 当 11 3[ , ] ,2 [ , ], ( )3 24 6 2 4x x f x      时 为减函数， 所以 11( ) [ , ] ( ) 2.4 4 3f x f   在 上的最大值为 又因为 11( ) 3, ( ) 2,4 24f f   故 11( ) [ , ]4 24f x  在 上的最小值为 11( ) 2.24f   2010 年高考题 一、选择题 1. （ 2010 全 国 卷 2 理 ） （ 7 ） 为 了 得 到 函 数 sin(2 )3y x   的 图 像 ， 只 需 把 函 数 sin(2 )6y x   的图像 （A）向左平移 4  个长度单位 （B）向右平移 4  个长度单位 （C）向左平移 2  个长度单位 （D）向右平移 2  个长度单位 【答案】B 【命题意图】本试题主要考查三角函数图像的平移. 【 解 析 】 sin(2 )6y x   = sin 2( )12x  ， sin(2 )3y x   = sin 2( )6x   ， 所 以 将 sin(2 )6y x   的图像向右平移 4  个长度单位得到 sin(2 )3y x   的图像，故选 B. 2.（2010 陕西文）3.函数 f (x)=2sinxcosx 是 (A)最小正周期为 2π的奇函数 （B）最小正周期为 2π的偶函数 (C)最小正周期为π的奇函数 （D）最小正周期为π的偶函数 【答案】C 解析：本题考查三角函数的性质 f (x)=2sinxcosx=sin2x，周期为π的奇函数 3.（2010 辽宁文）（6）设 0  ,函数 sin( ) 23y x    的图像向右平移 4 3  个单位后 与原图像重合，则 的最小值是 （A） 2 3 （B） 4 3 （C） 3 2 （D） 3 【答案】 C 解析：选 C.由已知，周期 2 4 3, .3 2T       4.（2010 辽宁理）（5）设 >0,函数 y=sin( x+ 3  )+2 的图像向右平移 3 4 个单位后与原 图像重合，则 的最小值是 （A） 2 3 (B) 4 3 (C) 3 2 (D)3 【答案】C 【命题立意】本题考查了三角函数图像的平移变换与三角函数的周期性，考查了同学们对知 识灵活掌握的程度。 【 解 析 】 将 y=sin(  x+ 3  )+2 的 图 像 向 右 平 移 3 4 个 单 位 后 为 4sin[ ( ) ] 23 3y x      4sin( ) 23 3x      ，所以有 4 3  =2k ,即 3 2 k  ， 又因为 0  ，所以 k≥1,故 3 2 k  ≥ 3 2 ，所以选 C 5.（2010 重庆文）（6）下列函数中，周期为 ，且在[ , ]4 2   上为减函数的是 （A） sin(2 )2y x   （B） cos(2 )2y x   （C） sin( )2y x   （D） cos( )2y x   【答案】 A 解析：C、D 中函数周期为 2 ，所以错误 当 [ , ]4 2x   时， 32 ,2 2x        ，函数 sin(2 )2y x   为减函数 而函数 cos(2 )2y x   为增函数，所以选 A 6.（2010 重庆理） （6）已知函数  sin ( 0, )2y x        的部分图 象如题（6）图所示，则 A.  =1  = 6  B.  =1  =- 6  C.  =2  = 6  D.  =2  = - 6  解 析 ： 2 T 由 五 点 作 图 法 知 232   ， = - 6  7.（2010 山东文）（10）观察 2 '( ) 2x x ， 4 ' 3( ) 4x x ， '(cos ) sinx x  ，由归纳推理可 得：若定义在 R 上的函数 ( )f x 满足 ( ) ( )f x f x  ，记 ( )g x 为 ( )f x 的导函数，则 ( )g x = （A） ( )f x (B) ( )f x (C) ( )g x (D) ( )g x 【答案】D 8.（2010 四川理）（6）将函数 siny x 的图像上所有的点向右平行移动 10  个单位长度， 再把所得各点的横坐标伸长到原来的 2 倍（纵坐标不变），所得图像的函数解析式是 （A） sin(2 )10y x   （B） sin(2 )5y x   （C） 1sin( )2 10y x   （D） 1sin( )2 20y x   解析：将函数 siny x 的图像上所有的点向右平行移动 10  个单位长度，所得函数图象的解 析式为 y＝sin(x－ 10  ) 再把所得各点的横坐标伸长到原来的 2 倍（纵坐标不变），所得图像的函数解析式是 1sin( )2 10y x   . 【答案】C 9.（2010 天津文）（8） 5y Asin x x R 6 6          右图是函数 （ + ）（ ）在区间 - ， 上的图象，为 了 得 到 这 个 函数的图象，只要将 y sin x x R （ ）的图象上所有的点 (A)向左平移 3  个单位长度，再把所得各点的横坐标缩短到 原来的 1 2 倍，纵坐标不变 (B) 向左平移 3  个单位长度，再把所得各点的横坐标伸长 到原来的 2 倍，纵坐标不变 (C) 向左平移 6  个单位长度，再把所得各点的横坐标缩短到原来的 1 2 倍，纵坐标不变 (D) 向左平移 6  个单位长度，再把所得各点的横坐标伸长到原来的 2 倍，纵坐标不变 【答案】A 【解析】本题主要考查三角函数的图像与图像变换的基础知识，属于中等题。 由图像可知函数的周期为 ，振幅为 1，所以函数的表达式可以是 y=sin(2x+ ).代入（- 6  ， 0）可得 的一个值为 3  ，故图像中函数的一个表达式是 y=sin(2x+ 3  )，即 y=sin2(x+ 6  )， 所以只需将 y=sinx（x∈R）的图像上所有的点向左平移 6  个单位长度，再把所得各点的横 坐标缩短到原来的 1 2 倍，纵坐标不变。 【温馨提示】根据图像求函数的表达式时，一般先求周期、振幅，最后求 。三角函数图像 进行平移变换时注意提取 x 的系数，进行周期变换时，需要将 x 的系数变为原来的 1  10.（2010 福建文） 11.（2010 四川文）（7）将函数 siny x 的图像上所有的点向右平行移动 10  个单位长度， 再把所得各点的横坐标伸长到原来的 2 倍（纵坐标不变），所得图像的函数解析式是 （A） sin(2 )10y x   （B） y  sin(2 )5x  （C） y  1sin( )2 10x  （D） 1sin( )2 20y x   【答案】C 解析：将函数 siny x 的图像上所有的点向右平行移动 10  个单位长度，所得函数图象的解 析式为 y＝sin(x－ 10  ) 再把所得各点的横坐标伸长到原来的 2 倍（纵坐标不变），所 得图像的函数解析式是 1sin( )2 10y x   . 12.（2010 湖北文）2.函数 f(x)= 3sin( ),2 4 x x R  的最小正周期为 A. 2  B.x C.2 D.4 【答案】D 【解析】由 T=| 2 1 2  |=4π，故 D 正确. 13.（2010 福建理）1． cos13 计算sin43 cos43 -sin13 的值等于（ ） A． 1 2 B． 3 3 C． 2 2 D． 3 2 【答案】A 【解析】原式= 1sin (43 -13 )=sin30 = 2    ，故选 A。 【命题意图】本题考查三角函数中两角差的正弦公式以及特殊角的三角函数，考查基础 知识，属保分题。 二、填空题 1.（2010 浙江理）（11）函数 2( ) sin(2 ) 2 2 sin4f x x x   的最小正周期是 __________________ . 解析：   242sin2 2       xxf 故最小正周期为π，本题主要考察了三角恒等变换及 相关公式，属中档题 2.（2010 浙江文）（12）函数 2( ) sin (2 )4f x x   的最小正周期是 。 答案 2  3.（2010 福建文）16.观察下列等式： ① cos2a=2 2cos a -1; ② cos4a=8 4cos a - 8 2cos a + 1; ③ cos6a=32 6cos a - 48 4cos a + 18 2cos a - 1; ④ cos8a=128 8cos a - 256 6cos a + 160 4cos a - 32 2cos a + 1; ⑤ cos10a= m 10cos a - 1280 8cos a + 1120 6cos a + n 4cos a + p 2cos a - 1． 可以推测，m – n + p = ． 【答案】962 【解析】因为 12 2 , 38 2 , 532 2 , 7128 2 , 所以 92 512m   ；观察可得 400n   ， 50p  ，所以 m – n + p =962。 【命题意图】本小题考查三角变换、类比推理等基础知识，考查同学们的推理能力等。 4.（2010 山东理） 5.（2010 福建理）14．已知函数 f(x)=3sin( x- )( >0)6   和 g(x)=2cos(2x+ )+1 的图象 的对称轴完全相同。若 x [0, ]2  ，则 f(x) 的取值范围是 。 【答案】 3[- ,3]2 【解析】由题意知， 2  ，因为 x [0, ]2  ，所以 52x- [- , ]6 6 6    ，由三角函数图象知： f(x) 的最小值为 33sin (- )=-6 2  ，最大值为3sin =32  ，所以 f(x) 的取值范围是 3[- ,3]2 。 6.（2010 江苏卷）10、定义在区间      20 , 上的函数 y=6cosx 的图像与 y=5tanx 的图像的交 点为 P，过点 P 作 PP1⊥x 轴于点 P1，直线 PP1 与 y=sinx 的图像交于点 P2,则线段 P1P2 的长为 ____________。 解析 考查三角函数的图象、数形结合思想。线段 P1P2 的长即为 sinx 的值， 且其中的 x 满足 6cosx=5tanx，解得 sinx= 2 3 。线段 P1P2 的长为 2 3 三、解答题 1.（2010 湖南文）16. （本小题满分 12 分） 已知函数 2( ) sin 2 2sinf x x x  （I）求函数 ( )f x 的最小正周期。 (II) 求函数 ( )f x 的最大值及 ( )f x 取最大值时 x 的集合。 2.（2010 浙江理）（18）(本题满分 l4 分)在△ABC 中,角 A、B、C 所对的边分别为 a,b,c， 已知 1cos2 4C   (I)求 sinC 的值； (Ⅱ)当 a=2， 2sinA=sinC 时，求 b 及 c 的长． 解析：本题主要考察三角变换、正弦定理、余弦定理等基础知识，同事考查运算求解能力。 （Ⅰ）解：因为 cos2C=1-2sin2C= 1 4  ，及 0＜C＜π 所以 sinC= 10 4 . （Ⅱ）解：当 a=2，2sinA=sinC 时，由正弦定理 a c sin A sin C  ，得 c=4 由 cos2C=2cos2C-1= 1 4  ，J 及 0＜C＜π得 cosC=± 6 4 由余弦定理 c2=a2+b2-2abcosC，得 b2± 6 b-12=0 解得 b= 6 或 2 6 所以 b= 6 b= 6 c=4 或 c=4 3.（2010 江西理）17.（本小题满分 12 分） 已知函数     21 cot sin sin sin4 4f x x x m x x               。 (1) 当 m=0 时，求  f x 在区间 3 8 4       ， 上的取值范围； (2) 当 tan 2a  时，   3 5f a  ，求 m 的值。 【解析】考查三角函数的化简、三角函数的图像和性质、已知三角函数值求值问题。依托三 角函数化简，考查函数值域，作为基本的知识交汇问题，考查基本三角函数变换，属于中等 题. 解：（1）当 m=0 时， 2 2cos 1 cos2 sin 2( ) (1 )sin sin sin cossin 2 x x xf x x x x xx       1[ 2 sin(2 ) 1]2 4x    ，由已知 3[ , ]8 4x   ，得 22 [ ,1]4 2x    从而得： ( )f x 的值域为 1 2[0, ]2  （2） 2cos( ) (1 )sin sin( )sin( )sin 4 4 xf x x m x xx       化简得： 1 1( ) [sin 2 (1 )cos2 ]2 2f x x m x    当 tan 2  ，得： 2 2 2 2sin cos 2tan 4sin 2 sin cos 1 tan 5 a a aa a a a     ， 3cos2 5a  ， 代入上式，m=-2. 4.（2010 浙江文）（18）（本题满分）在△ABC 中，角 A，B，C 所对的边分别为 a,b,c,设 S 为△ABC 的面积，满足 2 2 23 ( )4S a b c   。 （Ⅰ）求角 C 的大小； （Ⅱ）求sin sinA B 的最大值。 5.（2010 北京文）（15）（本小题共 13 分） 已知函数 2( ) 2cos2 sinf x x x  （Ⅰ）求 ( )3f  的值； （Ⅱ）求 ( )f x 的最大值和最小值 解：（Ⅰ） 22( ) 2cos sin3 3 3f     = 3 11 4 4     （Ⅱ） 2 2( ) 2(2cos 1) (1 cos )f x x x    23cos 1,x x R   因为  cos 1,1x  ,所以，当 cos 1x   时 ( )f x 取最大值 2；当 cos 0x  时， ( )f x 去最小值-1。 6.（2010 北京理）（15）（本小题共 13 分） 已知函数 (x)f 22cos2 sin 4cosx x x   。 （Ⅰ）求 ( )3f  的值； （Ⅱ）求 (x)f 的最大值和最小值。 解：（I） 22 3 9( ) 2cos sin 4cos 13 3 3 3 4 4f            （II） 2 2( ) 2(2cos 1) (1 cos ) 4cosf x x x x     = 23cos 4cos 1x x  = 22 73(cos )3 3x   , x R 因为 cos x  [ 1,1] ， 所以，当 cos 1x   时， ( )f x 取最大值 6；当 2cos 3x  时， ( )f x 取最小值 7 3  7.（2010 广东理）16、（本小题满分 14 分） 已知函数 ( ) sin(3 )( 0, ( , ),0f x A x A x          在 12x  时取得最大值 4． (1) 求 ( )f x 的最小正周期； (2) 求 ( )f x 的解析式； (3) 若 f ( 2 3 α + 12  )=12 5 ,求 sinα． 3sin(2 )2 5    ， 3cos2 5   ， 2 31 2sin 5   ， 2 1sin 5   ， 5sin 5    ． 8.（2010 广东文） 9.（2010 湖北文）16.（本小题满分 12 分） 已经函数 2 2cos sin 1 1( ) , ( ) sin 2 .2 2 4 x xf x g x x   (Ⅰ)函数 ( )f x 的图象可由函数 ( )g x 的图象经过怎样变化得出？ （Ⅱ）求函数 ( ) ( ) ( )h x f x g x  的最小值，并求使用 ( )h x 取得最小值的 x 的集合。 10.（2010 湖南理）16．（本小题满分 12 分） 已知函数 2( ) 3sin 2 2sinf x x x  ． （Ⅰ）求函数 ( )f x 的最大值； （II）求函数 ( )f x 的零点的集合。 2009 年高考题 一、选择题 1.(2009 年广东卷文)函数 1)4(cos2 2  xy 是 A．最小正周期为 的奇函数 B. 最小正周期为 的偶函数 C. 最小正周期为 2  的奇函数 D. 最小正周期为 2  的偶函数 答案 A 解析 因为 22cos ( ) 1 cos 2 sin 24 2y x x x          为奇函数, 2 2T    , 所以选 A. 2.（2009 全国卷Ⅰ理）如果函数  cos 2y x ＝3 ＋ 的图像关于点 4 3      ，0 中心对称，那么 | | 的最小值为（ ） A . 6  B. 4  C. 3  D. 2  答案 C 解析: 函数  cos 2y x ＝3 ＋ 的图像关于点 4 3      ，0 中心对称 42 3 k      42 ( )3k k Z      由此易得 min| | 3   .故选 C 3.（2009 全国卷Ⅰ理）若 4 2x   ，则函数 3tan 2 tany x x 的最大值为 。 答案 -8 解析:令 tan ,x t 14 2x t     , 4 4 3 2 2 2 4 2 2 2tan 2 2 2 2tan 2 tan 81 1 1 1 1 11 tan 1 ( )2 4 4 x ty x x x t t t t               4..（2009 浙江理）已知 a 是实数，则函数 ( ) 1 sinf x a ax  的图象不可能．．．是 ( ) 答案 D 解析 对于振幅大于 1 时，三角函数的周期为 2 , 1, 2T a Ta      ，而 D 不符合要求，它 的振幅大于 1，但周期反而大于了 2 ． 5..（2009 浙江文）已知 a 是实数，则函数 ( ) 1 sinf x a ax  的图象不可能．．．是（ ） 【命题意图】此题是一个考查三角函数图象的问题，但考查的知识点因含有参数而丰富，结 合图形考查使得所考查的问题形象而富有深度． 答案 D 解析 对于振幅大于 1 时，三角函数的周期为 2 , 1, 2T a Ta      ，而 D 不符合要求， 它的振幅大于 1，但周期反而大于了 2 ． 6.(2009 山东卷理)将函数 sin 2y x 的图象向左平移 4  个单位, 再向上平移1 个单位,所得 图象的函数解析式是( ). A. cos2y x B. 22cosy x C. )42sin(1  xy D. 22siny x 答案 B 解析 将函数 sin 2y x 的图象向左平移 4  个单位,得到函数 sin 2( )4y x   即 sin(2 ) cos22y x x   的图象,再向上平移 1 个单位,所得图象的函数解析式为 21 cos2 2cosy x x   ,故选 B. 【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析 式的基本知识和基本技能,学会公式的变形. 7.(2009 山东卷文)将函数 sin 2y x 的图象向左平移 4  个单位, 再向上平移1 个单位,所得 图象的函数解析式是( ). A. 22cosy x B. 22siny x C. )42sin(1  xy D. cos2y x 答案 A 解析 将函数 sin 2y x 的图象向左平移 4  个单位,得到函数 sin 2( )4y x   即 sin(2 ) cos22y x x   的图象,再向上平移 1 个单位,所得图象的函数解析式为 21 cos2 2cosy x x   ,故选 A. 【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析 式的基本知识和基本技能,学会公式的变形. 8.（2009 安徽卷理）已知函数 ( ) 3sin cos ( 0)f x x x     ， ( )y f x 的图像与直线 2y  的两个相邻交点的距离等于 ，则 ( )f x 的单调递增区间是 A. 5[ , ],12 12k k k Z     B. 5 11[ , ],12 12k k k Z     C.[ , ],3 6k k k Z     D. 2[ , ],6 3k k k Z     答案 C 解析 ( ) 2sin( )6f x x   ，由题设 ( )f x 的周期为T  ，∴ 2  ， 由 2 2 22 6 2k x k        得， ,3 6k x k k z       ，故选 C 9..（2009 安徽卷文）设函数 ，其中 ，则 导数 的取值范围是 A. B. C. D. 答案 D 解析 2 1(1) sin 3 cos xf x x       sin 3 cos 2sin( )3       5 20, sin( ) ,1 (1) 2,212 3 2 f                     ，选 D 10.（2009 江西卷文）函数 ( ) (1 3 tan )cosf x x x  的最小正周期为 A． 2 B． 3 2  C． D． 2  答案：A 解析 由 ( ) (1 3 tan )cos cos 3sin 2sin( )6f x x x x x x       可得最小正周期为 2 ,故选 A. 11.（2009 江西卷理）若函数 ( ) (1 3 tan )cosf x x x  ，0 2x   ，则 ( )f x 的最大值为 A．1 B． 2 C． 3 1 D． 3 2 答案：B 解析 因为 ( ) (1 3 tan )cosf x x x  = cos 3sinx x = 2cos( )3x  当 3x  是，函数取得最大值为 2. 故选 B 12.(2009 湖北卷理)函数 cos(2 ) 26y x    的图象 F 按向量 a 平移到 'F , 'F 的函数解析 式为 ( ),y f x 当 ( )y f x 为奇函数时，向量 a 可以等于 .( , 2)6A   .( ,2)6B  .( , 2)6C   .( ,2)6D  答案 B 解析 直接用代入法检验比较简单.或者设 ( , )a x y v ，根据定义 cos[2( ) ] 26y y x x       ，根据 y 是奇函数，对应求出 x ， y 13.（2009 全国卷Ⅱ理）若将函数  tan 04y x        的图像向右平移 6  个单位长度 后，与函数 tan 6y x      的图像重合，则 的最小值为 A． 1 6 B. 1 4 C. 1 3 D. 1 2 解析： 6tan tan[ ( ] ta)64 4 6ny x y x x                      向右平移 个单位 164 ( )6 6 2k k k Z           ， 又 min 10 2     .故选 D 答案 D 14..（2009 福建卷理）函数 ( ) sin cosf x x x 最小值是 ( ) A．-1 B. 1 2  C. 1 2 D.1 答案 B 解析 ∵ 1( ) sin 22f x x ∴ min 1( ) 2f x   .故选 B 15.（2009 辽宁卷理）已知函数 ( )f x =Acos( x  )的图象如图所示， 2( )2 3f    ，则 (0)f =( ) A. 2 3  B. 2 3 C.－ 1 2 D. 1 2 解析 由图象可得最小正周期为2π 3 于是 f(0)＝f(2π 3 ),注意到2π 3 与π 2 关于7π 12 对称 所以 f(2π 3 )＝－f(π 2 )＝ 2 3 答案 B 16.（2009 全国卷Ⅰ文）如果函数 3cos(2 )y x   的图像关于点 4( ,0)3  中心对称，那么  的最小值为 A. 6  B. 4  C. 3  D. 2  【解析】本小题考查三角函数的图象性质，基础题。 解: 函数  cos 2y x ＝3 ＋ 的图像关于点 4 3      ，0 中心对称 42 3 2k       13 ( )6k k Z     由此易得 min| | 6   .故选 A 17.（2009 湖北卷文）函数 2)62cos(  xy 的图像 F 按向量 a 平移到 F/，F/的解析式 y=f(x), 当 y=f(x)为奇函数时，向量 a 可以等于 A. )2,6(  B. )2,6( C. )2,6(   D. )2,6(  答案 D 解析 由平面向量平行规律可知，仅当 ( ,2)6a   时， F ： ( ) cos[2( ) ] 26 6f x x      = sin 2x 为奇函数，故选 D. 18.(2009 湖南卷理)将函数 y=sinx 的图象向左平移 ( 0   ＜2 ) 的单位后，得到函数 y=sin ( )6x  的图象，则 等于 （D） A． 6  B． 5 6  C. 7 6  D.11 6  答案 D 解析 由函数 siny x 向左平移 的单位得到 sin( )y x   的图象，由条件知函数 sin( )y x   可化为函数 sin( )6y x   ，易知比较各答案，只有 11sin( )6y x   sin( )6x   ，所以选 D 项 19.（2009 天津卷理）已知函数 ( ) sin( )( , 0)4f x x x R     的最小正周期为 ，为 了得到函数 ( ) cosg x x 的图象，只要将 ( )y f x 的图象 A 向左平移 8  个单位长度 B 向右平移 8  个单位长度 C 向左平移 4  个单位长度 D 向右平移 4  个单位长度 【考点定位】本小题考查诱导公式、函数图象的变换，基础题。 解析：由题知 2 ，所以 )8(2cos)42cos()]42(2cos[)42sin()(   xxxxxf ，故选择 A 答案 A 二、填空题 20.（2009 江苏卷）函数 sin( )y A x   （ , ,A   为常数， 0, 0A   ）在闭区间[ ,0] 上的图象如图所示，则 = . 答案 3 解析 考查三角函数的周期知识 3 2T  ， 2 3T  ，所以 3  ， 21（2009 宁夏海南卷理）已知函数 y=sin（ x+ ）（ >0, -   < ）的图像如图所 示，则  =________________ 答案： 9 10  解析：由图可知，  5 4 4, , 2 ,12 5 5 8 9,5 10 T x                    把 代入y=sin 有： 1=sin 22.（2009 宁夏海南卷文）已知函数 ( ) 2sin( )f x x   的图像如图所示，则 7 12f      。 答案 0 解析 由图象知最小正周期 T＝ 3 2 （ 44 5   ）＝ 3 2 ＝  2 ，故 ＝3，又 x＝ 4  时，f（x） ＝0，即 2   43sin( ）＝0，可得 4   ，所以， 7 12f      2 )412 73sin(   ＝0 23.(2009 湖南卷理)若 x∈(0, 2  )则 2tanx+tan( 2  -x)的最小值为 答案 2 2 解析 由 (0, )2x  ，知 1tan 0,tan( ) cot 0,2 tan         所以 12tan tan( ) 2tan 2 2,2 tan         当且仅当 tan 2 时取等号，即最小值是 2 2 24.（2009 年上海卷理）函数 22cos sin 2y x x  的最小值是_____________________ . 答案 1 2 解析 ( ) cos2 sin 2 1 2 sin(2 ) 14f x x x x       ，所以最小值为：1 2 25.（2009 年上海卷理）当 时10  x ，不等式 kxx  2sin  成立，则实数 k 的取值范围是 _______________. 答案 k≤1 解析 作出 2sin1 xy  与 kxy 2 的图象，要使不等式 kxx  2sin  成立，由图可知须 k≤1 26．（2009 年上海 卷理）已知函数 xxxf tansin)(  .项数为 27 的等差数列 na 满足      22  ，na ，且公差 0d .若 0)()()( 2721  afafaf ， 则当 k =____________是， 0)( kaf . 答案 14 解析 函数 xxxf tansin)(  在 ( )2 2   ， 是增函数，显然又为奇函数，函数图象关于原 点对称，因为 14262271 2aaaaa  ， 所以 1 27 2 26 14( ) ( ) ( ) ( ) ( ) 0f a f a f a f a f a       ，所以当 14k  时， 0)( kaf . 27.（2009 上海卷文）函数 2( ) 2cos sin 2f x x x  的最小值是 。 答案 1 2 解析 ( ) cos2 sin 2 1 2 sin(2 ) 14f x x x x       ，所以最小值为：1 2 28.（2009 辽宁卷文）已知函数 ( ) sin( )( 0)f x x     的图象如图所示， 则 ＝ 解析 由图象可得最小正周期为4π 3 ∴T＝2π ω ＝4π 3  ω＝ 2 3 答案 2 3 三、解答题 29.（2009 全国卷Ⅰ理）在 ABC 中，内角 A、B、C 的对边长分别为 a 、b 、 c ，已知 2 2 2a c b  ，且sin cos 3cos sin ,A C A C 求 b 分析:此题事实上比较简单,但考生反应不知从何入手.对已知条件(1) 2 2 2a c b  左侧是 二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2) sin cos 3cos sin ,A C A C 过多的关注两角和与差的正弦公式,甚至有的学生还想用现在 已经不再考的积化和差,导致找不到突破口而失分. 解法一：在 ABC 中 sin cos 3cos sin ,A C A C 则由正弦定理及余弦定理 有: 2 2 2 2 2 2 3 ,2 2 a b c b c aa cab bc      化简并整理得： 2 2 22( )a c b  .又由已知 2 2 2a c b  24b b  .解得 4 0(b b 或 舍）. 解法二:由余弦定理得: 2 2 2 2 cosa c b bc A   .又 2 2 2a c b  , 0b  。 所以 2 cos 2b c A  …………………………………① 又sin cos 3cos sinA C A C ， sin cos cos sin 4cos sinA C A C A C   sin( ) 4cos sinA C A C  ，即sin 4cos sinB A C 由正弦定理得sin sinbB Cc  ，故 4 cosb c A ………………………② 由①，②解得 4b  。 评析:从 08 年高考考纲中就明确提出要加强对正余弦定理的考查.在备考中应注意总结、提 高自己对问题的分析和解决能力及对知识的灵活运用能力.另外提醒：两纲中明确不再考的 知识和方法了解就行，不必强化训练。 30.（2009 北京文）（本小题共 12 分）已知函数 ( ) 2sin( )cosf x x x  . （Ⅰ）求 ( )f x 的最小正周期； （Ⅱ）求 ( )f x 在区间 ,6 2      上的最大值和最小值. 解析 本题主要考查特殊角三角函数值、诱导公式、二倍角的正弦、三角函数在闭区间上的 最值等基础知识，主要考查基本运算能力． 解（Ⅰ）∵    2sin cos 2sin cos sin 2f x x x x x x    ， ∴函数 ( )f x 的最小正周期为 . （Ⅱ）由 26 2 3x x          ，∴ 3 sin 2 12 x   ， ∴ ( )f x 在区间 ,6 2      上的最大值为 1，最小值为 3 2  . 31.（2009 北京理）（本小题共 13 分） 在 ABC 中，角 , ,A B C 的对边分别为 , , , 3a b c B  ， 4cos , 35A b  。 （Ⅰ）求sinC 的值； （Ⅱ）求 ABC 的面积. 解析 本题主要考查三角形中的三角函数变换及求值、诱导公式、三角形的面积公式等基础 知识，主要考查基本运算能力． 解（Ⅰ）∵A、B、C 为△ABC 的内角，且 4,cos3 5B A  ， ∴ 2 3,sin3 5C A A   ， ∴ 2 3 1 3 4 3sin sin cos sin3 2 2 10C A A A         . （Ⅱ）由（Ⅰ）知 3 3 4 3sin ,sin5 10A C   ， 又∵ , 33B b  ，∴在△ABC 中，由正弦定理， ∴ sin 6 sin 5 b Aa B   . ∴△ABC 的面积 1 1 6 3 4 3 36 9 3sin 32 2 5 10 50S ab C        32.（2009 江苏卷） 设向量 (4cos ,sin ), (sin ,4cos ), (cos , 4sin )a b c           （1）若 a  与 2b c  垂直，求 tan( )  的值； （2）求| |b c  的最大值; （3）若 tan tan 16   ，求证： a  ∥b  . 【解析】 本小题主要考查向量的基本概念，同时考查同角三角函数的基本关系式、二倍角 的正弦、两角和的正弦与余弦公式，考查运算和证明得基本能力。满分 14 分。 33.(2009 山东卷理)(本小题满分 12 分)设函数 f(x)=cos(2x+ 3  )+sin 2 x. (1) 求函数 f(x)的最大值和最小正周期. (2) 设 A,B,C 为  ABC 的三个内角，若 cosB= 3 1 ， 1( )2 4 cf   ，且 C 为锐角，求 sinA. 解: （1） f(x)=cos(2x+ 3  )+sin 2 x.= 1 cos2 1 3cos2 cos sin 2 sin sin 23 3 2 2 2 xx x x      所以函数 f(x)的最大值为1 3 2  ,最小正周期 . （2） ( )2 cf = 1 3 sin2 2 C =－ 4 1 , 所以 3sin 2C  , 因为 C 为锐角, 所以 3C  , 又因为在  ABC 中, cosB= 3 1 , 所以 2sin 33B  , 所以 2 1 1 3 2 2 3sin sin( ) sin cos cos sin 23 2 3 2 6A B C B C B C          . 【命题立意】:本题主要考查三角函数中两角和差的弦函数公式、二倍角公式、三角函数的 性质以及三角形中的三角关系. 34.(2009 山东卷文)(本小题满分 12 分)设函数 f(x)=2 )0(sinsincos2cossin 2   xxx 在 x 处取最小值. （1） 求 .的值; （2） 在  ABC 中, cba ,, 分别是角 A,B,C 的对边,已知 ,2,1  ba 2 3)( Af ,求 角 C.. 解: （1） 1 cos( ) 2sin cos sin sin2f x x x x     sin sin cos cos sin sinx x x x     sin cos cos sinx x   sin( )x   因为函数 f(x)在 x 处取最小值，所以 sin( ) 1    ,由诱导公式知sin 1  ,因为 0    ,所以 2   .所以 ( ) sin( ) cos2f x x x   （2）因为 2 3)( Af ,所以 3cos 2A  ,因为角 A 为  ABC 的内角,所以 6A  .又因为 ,2,1  ba 所以由正弦定理,得 sin sin a b A B  ,也就是 sin 1 2sin 2 2 2 b AB a     , 因为b a ,所以 4 B 或 4 3B . 当 4 B 时, 7 6 4 12C       ;当 4 3B 时, 3 6 4 12C       . 【命题立意】:本题主要考查了三角函数中两角和差的弦函数公式、二倍角公式和三角函数 的性质,并利用正弦定理解得三角形中的边角.注意本题中的两种情况都符合. 35.(2009 全国卷Ⅱ文）（本小题满分 12 分）设△ABC 的内角 A、B、C 的对边长分别为 a、b、 c， 2 3cos)cos(  BCA , acb 2 ，求 B. 解析：本题考查三角函数化简及解三角形的能力，关键是注意角的范围对角的三角函数值的 制约，并利用正弦定理得到 sinB= 2 3 (负值舍掉)，从而求出 B= 3  。 解：由 cos（A  C）+cosB= 3 2 及 B=π  （A+C） cos（A  C）  cos（A+C）= 3 2 ， cosAcosC+sinAsinC  （cosAcosC  sinAsinC）= 3 2 , sinAsinC= 3 4 . 又由 2b =ac 及正弦定理得 2sin sin sin ,B A C 故 2 3sin 4B  ， 3sin 2B  或 3sin 2B   （舍去）， 于是 B= 3 π 或 B= 2 3 π. 又由 2b ac 知 ab  或 cb  所 以 B= 3 π。 36.(2009 江西卷文）（本小题满分 12 分） 在△ ABC 中， , ,A B C 所对的边分别为 , ,a b c ， 6A  ， (1 3) 2c b  ． （1）求C ； （2）若 1 3CB CA    ，求 a ,b ， c ． 解：（1）由 (1 3) 2c b  得 1 3 sin 2 2 sin b B c C    则有 5 5sin( ) sin cos cos sin6 6 6 sin sin C C C C C        = 1 3 1 3cot2 2 2 2C    得 cot 1C  即 4C  . （2） 由 1 3CB CA    推出 cos 1 3ab C   ；而 4C  , 即得 2 1 32 ab   , 则有 2 1 32 (1 3) 2 sin sin ab c b a c A C           解得 2 1 3 2 a b c        37.（2009 江西卷理）△ ABC 中， , ,A B C 所对的边分别为 , ,a b c ， sin sintan cos cos A BC A B   ,sin( ) cosB A C  . （1）求 ,A C ； （2）若 3 3ABCS   ,求 ,a c . 解：(1) 因为 sin sintan cos cos A BC A B   ，即 sin sin sin cos cos cos C A B C A B   ， 所以sin cos sin cos cos sin cos sinC A C B C A C B   ， 即 sin cos cos sin cos sin sin cosC A C A C B C B   ， 得 sin( ) sin( )C A B C   . 所以C A B C   ,或 ( )C A B C    (不成立). 即 2C A B  , 得 3C  ，所以. 2 3B A   又因为 1sin( ) cos 2B A C   ，则 6B A   ，或 5 6B A   （舍去） 得 5,4 12A B   (2) 1 6 2sin 3 32 8ABCS ac B ac     ， 又 sin sin a c A C  , 即 2 3 2 2 a c ， 得 2 2, 2 3.a c  38.（2009 全国卷Ⅱ理）设 ABC 的内角 A 、 B 、C 的对边长分别为 a 、b 、 c ， 3cos( ) cos 2A C B   ， 2b ac ，求 B 。 分析：由 3cos( ) cos 2A C B   ，易想到先将 ( )B A C   代入 3cos( ) cos 2A C B   得 3cos( ) cos( ) 2A C A C    。 然后利用两角和与差的余弦公式展开得 3sin sin 4A C  ； 又由 2b ac ，利用正弦定理进行边角互化，得 2sin sin sinB A C ，进而得 3sin 2B  . 故 2 3 3B   或 。大部分考生做到这里忽略了检验，事实上，当 2 3B  时，由 1cos cos( ) 2B A C     ，进而得 3cos( ) cos( ) 2 12A C A C      ，矛盾，应舍去。 也可利用若 2b ac 则b a b c 或 从而舍去 2 3B  。不过这种方法学生不易想到。 评析：本小题考生得分易，但得满分难。 39.(2009 陕西卷理)（本小题满分 12 分） 已知函数 ( ) sin( ),f x A x x R    （其中 0, 0,0 2A      ）的图象与 x 轴的交 点中，相邻两个交点之间的距离为 2  ，且图象上一个最低点为 2( , 2)3M   . (Ⅰ)求 ( )f x 的解析式；（Ⅱ）当 [ , ]12 2x   ，求 ( )f x 的值域. 解（1）由最低点为 2( , 2)3M   得 A=2. 由 x 轴上相邻的两个交点之间的距离为 2  得 2 T = 2  ，即T  ， 2 2 2T      由点 2( , 2)3M   在图像上的 2 42sin(2 ) 2, ) 13 3         即sin( 故 4 2 ,3 2k k Z      112 6k     又 (0, ), , ( ) 2sin(2 )2 6 6f x x       故 （2） 7[ , ], 2 [ , ]12 2 6 3 6x x        　　　　 当 2 6x  = 2  ，即 6x  时， ( )f x 取得最大值 2；当 72 6 6x    即 2x  时， ( )f x 取得最小值-1，故 ( )f x 的值域为[-1,2] 40.（2009 湖北卷文）在锐角△ABC 中，a、b、c 分别为角 A、B、C 所对的边，且 Aca sin23  (Ⅰ)确定角 C 的大小： （Ⅱ）若 c＝ 7 ,且△ABC 的面积为 2 33 ,求 a＋b 的值。 解（1）由 3 2 sina c A 及正弦定理得， 2sin sin sin3 a A A c C   3sin 0, sin 2A C  Q ABCQ 是锐角三角形， 3C   （2）解法 1： 7, .3c C  Q 由面积公式得 1 3 3sin , 62 3 2ab ab  即 　　　　　　　　① 由余弦定理得 2 2 2 22 cos 7, 73a b ab a b ab     即 　　　　② 由②变形得 25, 5a b  2（a+b) 故 解法 2：前同解法 1，联立①、②得 2 2 2 27 6 6 a b ab a b ab ab         ＝１３　 消去 b 并整理得 4 213 36 0a a   解得 2 24 9a a 或 所以 2 3 3 2 a a b b        或 故 5a b  41.(2009 湖南卷理)在 ABC ，已知 22 3 3AB AC AB AC BC       ，求角 A，B，C 的 大小. 解：设 , ,BC a AC b AB c   由 2 3AB AC AB AC      得 2 cos 3bc A bc ，所以 3cos 2A  又 (0, ),A  因此 6A  由 23 3AB AC BC   得 23bc a ，于是 2 3sin sin 3sin 4C B A   所以 5 3sin sin( )6 4C C   ， 1 3 3sin ( cos sin )2 2 4C C C   ，因此 22sin cos 2 3sin 3,sin 2 3 cos2 0C C C C C     ，既sin(2 ) 03C   由 A= 6  知 50 6C   ，所以 3  ， 42 3 3C    ，从而 2 0,3C   或 2 ,3C    ，既 ,6C  或 2 ,3C  故 2, , ,6 3 6A B C     或 2, ,6 6 3A B C     42.（2009 福建卷文）.c.o.m 已知函数 ( ) sin( ),f x x   其中 0  ，| | 2   （I）若 cos cos, sin sin 0,4 4     求 的值； （Ⅱ）在（I）的条件下，若函数 ( )f x 的图像的相邻两条对称轴之间的距离等于 3  ，求 函数 ( )f x 的解析式；并求最小正实数 m ，使得函数 ( )f x 的图像象左平移 m 个单位所对应 的函数是偶函数。 解法一： （I） 由 3cos cos sin sin 04 4     得 cos cos sin sin 04 4     即 cos( ) 04    又| | ,2 4      （Ⅱ）由（I）得， ( ) sin( )4f x x   依题意， 2 3 T  又 2 ,T   故函数 ( )f x 的图像向左平移 m 个单位后所对应的函数为 ( ) sin 3( ) 4g x x m       ( )g x 是偶函数当且仅当3 ( )4 2m k k Z     即 ( )3 12 km k Z    从而，最小正实数 12m  解法二： （I）同解法一 （Ⅱ）由（I）得， ( ) sin( )4f x x   依题意， 2 3 T  又 2T   ，故 3, ( ) sin(3 )4f x x      函数 ( )f x 的图像向左平移 m 个单位后所对应的函数为 ( ) sin 3( ) 4g x x m       ( )g x 是偶函数当且仅当 ( ) ( )g x g x  对 x R 恒成立 亦即sin( 3 3 ) sin(3 3 )4 4x m x m       对 x R 恒成立。 sin( 3 )cos(3 ) cos( 3 )sin(3 )4 4x m x m       sin3 cos(3 ) cos3 sin(3 )4 4x m x m     即 2sin3 cos(3 ) 04x m   对 x R 恒成立。 cos(3 ) 04m    故3 ( )4 2m k k Z     ( )3 12 km k Z     从而，最小正实数 12m  43.（2009 重庆卷理）（本小题满分 13 分，（Ⅰ）小问 7 分，（Ⅱ）小问 6 分．） 设函数 2( ) sin( ) 2cos 14 6 8 x xf x       ． （Ⅰ）求 ( )f x 的最小正周期． （Ⅱ）若函数 ( )y g x 与 ( )y f x 的图像关于直线 1x  对称，求当 4[0, ]3x 时 ( )y g x 的最大值． 解：（Ⅰ） ( )f x =sin cos cos sin cos4 6 4 6 4x x x      = 3 3sin cos2 4 2 4x x  = 3sin( )4 3x  故 ( )f x 的最小正周期为 T = 2 4   =8 (Ⅱ)解法一： 在 ( )y g x 的图象上任取一点 ( , ( ))x g x ，它关于 1x  的对称点 (2 , ( ))x g x . 由题设条件，点 (2 , ( ))x g x 在 ( )y f x 的图象上，从而 ( ) (2 ) 3sin[ (2 ) ]4 3g x f x x      = 3sin[ ]2 4 3x    = 3 cos( )4 3x  当 30 4x  时， 2 3 4 3 3x      ，因此 ( )y g x 在区间 4[0, ]3 上的最大值为 max 33 cos 3 2g   解法二： 因区间 4[0, ]3 关于 x = 1 的对称区间为 2[ ,2]3 ，且 ( )y g x 与 ( )y f x 的图象关于 x = 1 对称，故 ( )y g x 在 4[0, ]3 上的最大值为 ( )y f x 在 2[ ,2]3 上的最大值 由（Ⅰ）知 ( )f x ＝ 3sin( )4 3x  当 2 23 x  时， 6 4 3 6        因此 ( )y g x 在 4[0, ]3 上的最大值为 max 33sin 6 2g   . 44.（2009 重庆卷文）（本小题满分 13 分，（Ⅰ）小问 7 分，（Ⅱ）小问 6 分．） 设函数 2 2( ) (sin cos ) 2cos ( 0)f x x x x       的最小正周期为 2 3  ． （Ⅰ）求 的最小正周期． （Ⅱ）若函数 ( )y g x 的图像是由 ( )y f x 的图像向右平移 2  个单位长度得到，求 ( )y g x 的单调增区间． 解：（Ⅰ） 2 2 2 2( ) (sin cos ) 2cos sin cos sin 2 1 2cos2f x x x x x x x x              sin 2 cos2 2 2 sin(2 ) 24x x x         依题意得 2 2 2 3     ，故 的最小正周期为 3 2 . （Ⅱ）依题意得: 5( ) 2 sin 3( ) 2 2 sin(3 ) 22 4 4g x x x            由 52 3 2 ( )2 4 2k x k k Z      ≤ ≤ 解得 2 2 7 ( )3 4 3 12k x k k Z    ≤ ≤ 故 ( )y g x 的单调增区间为: 2 2 7[ , ] ( )3 4 3 12k k k Z     45.（2009 上海卷文）（本题满分 14 分）本题共有 2 个小题，第 1 小题满分 6 分，第 2 小 题满分 8 分 . 已知ΔABC 的角 A、B、C 所对的边分别是 a、b、c，设向量 ( , )m a b ， (sin ,sin )n B A ， ( 2, 2)p b a   . （1） 若 m  // n  ，求证：ΔABC 为等腰三角形； （2） 若 m  ⊥ p  ，边长 c = 2，角 C = 3  ，求ΔABC 的面积 . 证明：（1） // , sin sin ,m n a A b B uv v Q 即 2 2 a ba bR R    ，其中 R 是三角形 ABC 外接圆半径， a b ABC 为等腰三角形 解（2）由题意可知 // 0, ( 2) ( 2) 0m p a b b a    uv uv 即 a b ab   由余弦定理可知， 2 2 24 ( ) 3a b ab a b ab      2( ) 3 4 0ab ab  即 4( 1)ab ab   舍去 1 1sin 4 sin 32 2 3S ab C       2008 年高考题 一、选择题 1.（2008 山东）函数 ln cos ( )2 2y x x     的图象是 （ ） 答案：A 解析 本题考查复合函数的图象。 ln cos 2 2y x x        是偶函数，可排除 B,D; 由 cos 1 ln cos 0x x   排除 C,选 A 2.（海南、宁夏理科卷）已知函数 2sin( )( 0)y x     )在区间 0 2， 的图像如下：那 么 ＝（ ） A．1 B．2 C． 2 1 D． 3 1 答案：B 解析 由图象知函数的周期T  ，所以 2 2T    3、（2008 广东）已知函数 2( ) (1 cos2 )sin ,f x x x x R   ，则 ( )f x 是（ ） A、最小正周期为 的奇函数 B、最小正周期为 2  的奇函数 C、最小正周期为 的偶函数 D、最小正周期为 2  的偶函数 答案：D 解析 2 2 2 21 1 cos4( ) (1 cos2 )sin 2cos sin sin 22 4 xf x x x x x x      4.（2008 海南、宁夏文科卷）函数 ( ) cos2 2sinf x x x  的最小值和最大值分别为（ ） y x2π 1 1 O A. －3，1 B. －2，2 C. －3， 3 2 D. －2， 3 2 解析 ∵   2 2 1 31 2sin 2sin 2 sin 2 2f x x x x          ∴当 1sin 2x  时，  max 3 2f x  ，当sin 1x   时，  min 3f x   ；故选Ｃ； 答案：C 5.（2007 福建）已知函数 ( ) sin ( 0)f x x       的最小正周期为  ，则该函数的图 象（ ） A．关于点 0     ， 对称 B．关于直线 x   对称 C．关于点 0     ， 对称 D．关于直线 x   对称 答案 A 6.（2007 广东）若函数 2 1( ) sin ( )2f x x x   R ，则 ( )f x 是（ ） A．最小正周期为 π 2 的奇函数 B．最小正周期为 π 的奇函数 C．最小正周期为 2π 的偶函数 D．最小正周期为 π 的偶函数 答案 D 7.（2007 海南、宁夏）函数 πsin 2 3y x     在区间 π π2     ， 的简图是（ ） 答案 A 8.（2007 浙江）若函数 ( ) 2sin( )f x x   ， xR （其中 0  ， 2   ）的最小正周 期是  ，且 (0) 3f  ，则（ ） A． 1 2 6    ， B． 1 2 3    ， C． 2 6    ， D． 2 3    ， 答案 D 二、填空题 12.（2008 江苏卷） ( ) cos( )6f x wx   的最小正周期为 5  ，其中 0w  ，则 w  答案：10 解析 本小题考查三角函数的周期公式。 2 105T ww      13.（广东理科卷）已知函数 ( ) (sin cos )sinf x x x x  ， xR ，则 ( )f x 的最小正周期 是 ． 答案： 解析 2 1 cos2 1( ) sin sin cos sin 22 2 xf x x x x x    ,所以函数的最小正周期 2 2T    。 14.（2007 安徽）函数 π( ) 3sin 2 3f x x     的图象为C ，如下结论中正确的是__________ （写出所有正确结论的编号．．）． ①图象 C 关于直线 11 π12x  对称； ②图象 C 关于点 2π 03      ， 对称； ③函数 ( )f x 在区间 π 5π 12 12     ， 内是增函数； ④由 3sin 2y x 的图角向右平移 π 3 个单位长度可以得到图象C 答案 ①②③ 15.（2007 四川）下面有五个命题： ①函数 y=sin4x-cos4x 的最小正周期是 . ②终边在 y 轴上的角的集合是{a|a= Zkk  ,2 ｝. ③在同一坐标系中，函数 y=sinx 的图象和函数 y=x 的图象有三个公共点. ④把函数 .2sin36)32sin(3 的图象得到的图象向右平移 xyxy  ⑤函数 .0)2sin( 〕上是减函数，在〔  xy 其中真命题的序号是 答案 ① ④ 三、解答题 16.（2008 山东）已知函数 f(x)＝ )0,0)(cos()sin(3   πxx 为偶函 数，且函数 y＝f(x)图象的两相邻对称轴间的距离为 .2 π （Ⅰ）求 f（ 8 π ）的值； （Ⅱ）将函数 y＝f(x)的图象向右平移 6 π 个单位后，再将得到的图象上各点的横坐标伸长到 原来的 4 倍，纵坐标不变，得到函数 y＝g(x)的图象，求 g(x)的单调递减区间. 解（Ⅰ）f(x)＝ )cos()sin(3   xx ＝        )cos(2 1)sin(2 32  xx ＝2sin(  x - 6 π ) 因为 f(x)为偶函数， 所以对 x∈R,f(-x)=f(x)恒成立， 因此 sin（-  x - 6 π ）＝sin(  x - 6 π ). 即-sin x cos( - 6 π )+cos x sin( - 6 π )=sin x cos( - 6 π )+cos x sin( - 6 π ), 整理得 sin x cos( - 6 π )=0.因为 ＞0，且 x∈R,所以 cos（ - 6 π ）＝0. 又因为 0＜ ＜π，故  - 6 π ＝ 2 π .所以 f(x)＝2sin( x + 2 π )=2cos x . 由题意得 2 2 2      ，所以 2　＝ 故 f(x)=2cos2x. 因为 .24cos2)8(  f （Ⅱ）将 f(x)的图象向右平移个 6  个单位后，得到 )6( xf 的图象，再将所得图象横坐标 伸长到原来的 4 倍，纵坐标不变，得到 )64(  f 的图象. 所以 ( ) ( ) 2cos 2( ) 2cos ( ).4 6 4 6 2 3g x f f              当 2 22 3k k       (k∈Z), 即 4kπ＋≤ 3 2 ≤x≤4kπ+ 3 8 (k∈Z)时，g(x)单调递减. 因此 g(x)的单调递减区间为      3 84,3 24  kk (k∈Z) 17.（2008 广东）已知函数 ( ) sin( )( 0 0 π)f x A x A     ， ， xR 的最大值是 1， 其图像经过点 π 1 3 2M      ， ． （1）求 ( )f x 的解析式； （2）已知 π0 2       ， ， ，且 3( ) 5f   ， 12( ) 13f   ，求 ( )f   的值． 解（1）依题意有 1A  ，则 ( ) sin( )f x x   ，将点 1( , )3 2M  代入得 1sin( )3 2    ， 而 0    ， 5 3 6      ， 2   ，故 ( ) sin( ) cos2f x x x   ； （2）依题意有 3 12cos ,cos5 13    ，而 , (0, )2    ， 2 23 4 12 5sin 1 ( ) ,sin 1 ( )5 5 13 13         ， 3 12 4 5 56( ) cos( ) cos cos sin sin 5 13 5 13 65f                  18.（2007 湖北）已知函数 2 π( ) cos 12f x x     ， 1( ) 1 sin 22g x x  ． （I）设 0x x 是函数 ( )y f x 图象的一条对称轴，求 0( )g x 的值． （II）求函数 ( ) ( ) ( )h x f x g x  的单调递增区间． 解：（I）由题设知 1 π( ) [1 cos(2 )]2 6f x x   ． 因为 0x x 是函数 ( )y f x 图象的一条对称轴，所以 0 π2 6x  πk ， 即 0 π2 π 6x k  （ k Z ）． 所以 0 0 1 1 π( ) 1 sin 2 1 sin( π )2 2 6g x x k     ． 当 k 为偶数时， 0 1 π 1 3( ) 1 sin 12 6 4 4g x          ， 当 k 为奇数时， 0 1 π 1 5( ) 1 sin 12 6 4 4g x      ． （II） 1 π 1( ) ( ) ( ) 1 cos 2 1 sin 22 6 2h x f x g x x x             1 π 3 1 3 1 3cos 2 sin 2 cos2 sin 22 6 2 2 2 2 2x x x x                    1 π 3sin 22 3 2x      ． 当 π π π2 π 2 2 π2 3 2k x k  ≤ ≤ ，即 5π ππ π12 12k x k ≤ ≤ （ k Z ）时， 函数 1 π 3( ) sin 22 3 2h x x      是增函数， 故函数 ( )h x 的单调递增区间是 5π ππ π12 12k k     ， （ k Z ）． 第二部分 四年联考汇编 2013-2014 年联考题 一、选择题 1、（绵阳市南山中学 2014 届高三上学期 12 月月考）要得到函数 xy cos3 的图象，只需 将函数 )62sin(3  xy 的图象上所有点的( ) A. 横坐标缩短到原来的 2 1 （纵坐标不变）,所得图象再向左平移 3 2 个单位长度. B. 横坐标缩短到原来的 2 1 （纵坐标不变），所得图象再向右平移 6  个单位长度. C. 横坐标伸长到原来的 2 倍(纵坐标不变),所得图象再向左平移 3 2 个单位长度. D. 横坐标伸长到原来的 2 倍(纵坐标不变)，所得图象再向右平移 6  个单位长度. 答案：C 2、（雅安中学 2014 届高三上学期 12 月月考）已知 3cossin cossin   xx xx ，则 xtan 的值是 A. 3 B . —3 C. 2 D. -2 答案：C 3、（成都七中 2014 届高三上期中考试）已知 ，则 =（ ） A． B． C． D． 答案：C 4、（绵阳市高中 2014 届高三 11 月第一次诊断性考试）已知函数 其中 k＞0，若当自变量 x 在任何两个整数间（包括整数本身）变化 时，至少含有 2 个周期，则 最小的正整数 k 为 A、50 B、51 C、12 D、13 答案：B 5、（成都石室中学 2014 届高三上学期期中）函数 )2sin(sin xxy   的最小正周期是（ ） A. B.  C. 2π D. 4π 答案：B 6、（成都市 2014 届高三上学期摸底）若 2costan 3, sin cos     则 的值为 A． -1 B． 1 2 C．l D．2 答案：B 7、（树德中学高 2014 届高三上学期期中）已知 3cos2 2   ，则 的值为 A． B． C． 3 2 D． 3 2  答案：D 8、（泸州市 2014 届高三第一次教学质量诊断）将函数 ( ) sin(2 )( )2 2f x x        的图象 向右平移 ( 0)   个单位长度后得到函数 ( )g x 的图象，若 ( )f x 、 ( )g x 的图象都经过点 3(0, )2P ，则 的值可以是 A． 5 3  B． 5 6  C． 2  D． 6  答案：B 9、（乐山市第一中学 2014 届高三 10 月月考）已知函数  =cos sin 2 ,f x x x 下列结论中正确的是 （ ） A、    ,0y f x  的图像关于 中心对称 B、   2y f x x  的图像关于 对称 C、   3 2f x 的最大值为 D、  f x 既是奇函数，又是周期函数 答案：C 10、（德阳中学 2014 届高三“零诊”考试） 把函数 sin(5 )2y x   的图象向右平移 4  个单位，再把所得函数图象上各点的横坐标缩短 为原来的 1 2 ，所得的函数解析式为( ) A． 3sin(10 )4y x   B． 7sin(10 )2y x   C． 7sin(10 )4y x   D． 3sin(10 )2y x   答案：C 11、（乐山市第一中学 2014 届高三 10 月月考）为了得到函数 Rxxy  ),63sin(2  的图像， 4 4sin cos 2 3 2 3  只需把函数 Rxxy  ,sin2 的图像上所有的点（ ） （A）向左平移 6  个单位长度，再把所得各点的横坐标缩短到原来的 3 1 倍（纵坐标不变） （B）向右平移 6  个单位长度，再把所得各点的横坐标缩短到原来的 3 1 倍（纵坐标不变） （C）向左平移 6  个单位长度，再把所得各点的横坐标伸长到原来的 3 倍（纵坐标不变） （D）向右平移 6  个单位长度，再把所得各点的横坐标伸长到原来的 3 倍（纵坐标不变） 答案：C 12、（泸州市 2014 届高三第一次教学质量诊断）函数 2 1( ) (1 )sinf x xx   的图象大致为 A． B． C． D． 答案：A 13、（绵阳市高中 2014 届高三 11 月第一次诊断性考试）下列不等式中，正确的是 A、sin1°＞cos1 B、sin1＞cos1° C、sin1＜sin2 D、sin2＜sin3 答案：C 14、（什邡中学高中 2014 届高三上学期第二次月考）将函数 ( ) sinf x x 图象上所有点的 横坐标伸长到原来的 2 倍，再向右平移 6  个单位长度，得到函数 ( )y g x 的图象，则 ( )y g x 图象的解析式是（ ） A． ( ) sin(2 )6g x x   B． ( ) sin(2 )3g x x   C． 1( ) sin( )2 12g x x   D． 1( ) sin( )2 6g x x   答案：X 15、（资阳市2014届高三上学期第一次诊断性考试） ABC 中，若 2 2 2sin sin sin sin sin 0B C A B C    ，则 A  （A） 2 3  （B） 5 6  （C） 3  （D） 6  答案：A 16、（资阳市 2014 届高三上学期第一次诊断性考试）若把函数 siny x （ 0  ）的图象 向左平移 3  个单位后与函数 cosy x 的图象重合，则 的值可能是 （A） 1 3 （B） 1 2 （C） 3 2 （D） 2 3 答案：C 17、（雅安中学 2014 届高三上学期 12 月月考）在ΔABC 中，角 A，B，C 所对的边的长分别为 cba ,, ， 若 CcBbAa sinsinsin  ，则 ΔABC 的形状是 A.锐角三角 B.直角三角形 C.钝角三角形 D.正三角形 答案：C 18、（绵阳市高中 2014 届高三 11 月第一次诊断性考试）已知 ,  都是锐角，且 5 4cos ,sin( )5 5      ，则 tan  为 A、2 B、－ 2 11 C、－ 2 11 或 2 D、 2 11 或－2 答案：A 二、填空题 1、（成都七中 2014 届高三上期中考试）已知 ， ，则 = ． 答案： 或 2、（成都七中 2014 届高三上期中考试）ΔABC 中，B=120º，AC=3，AB= ，则ΔABC 的面积为 ． 答案： 3、（成都七中 2014 届高三上期中考试）在平面直角坐标系中，已知角 的顶点在坐标原 点，始边在 轴的非负半轴上，终边经过点 ，则 答案： 4 、 （ 德 阳 中 学 2014 届 高 三 “ 零 诊 ” 考 试 ） 已 知 2 2 )4sin( )2cos(      ， 则 _______sincos   答案： 1 2  5、（乐山市第一中学 2014 届高三 10 月月考） 函数 ( ) sin( ),( , ,f x A x A     是常数， 0, 0)A   的部分图象如图所示，则 0f ( )  答案： 2 6 6、（乐山市第一中学 2014 届高三 10 月月考）设 为锐角， 若 4cos 6 5       ，则 )122sin( a 的值为 ． 答案： 17 250 7、（什邡中学高中 2014 届高三上学期第二次月考）设θ为第二象限角，若 tan(θ＋π 4)＝1 2 ， 则 sinθ＋cosθ＝ ． 答案： 10 5  8、（资阳市 2014 届高三上学期第一次诊断性考试）在平面直角坐标系中，角α的顶点与原 点重合，始边与x 轴的非负半轴重合，若角α终边经过点 (2,4)P ，则 tan( )4    ___________. 答案：－3 三、解答题， 1、（绵阳市南山中学 2014 届高三上学期 12 月月考） 已知函数 2 1cos2sin2 3)( 2  xxxf ， x R ． （I）若 ]4 3,24 5[ x ，求函数 ( )f x 的最大值和最小值，并写出相应的 x 的值； （II）设 ABC 的内角 A 、 B 、 C 的对边分别为 a 、b 、 c ，满足 3c  ， ( ) 0f C  且 sin 2sinB A ，求 a 、b 的值. 解（Ⅰ） 3 1 cos2 1( ) sin 2 sin(2 ) 12 2 2 6 xf x x x       …….............3 分 令 ,62  xt     3 4,4 t   1sin  ttf 。 当 2 t 即 3 x 时，   0max xf 当 3 4t 即 4 3x 时，   12 3 min xf ； ……6 分 （Ⅱ） ( ) sin(2 ) 1 06f C C     ，则sin(2 ) 1 06C    ， ……............7 分 0 C   , 0 2 2C   ,所以 1126 6 6C      ， 所以 2 6 2C    ， 3C  …….....................................................................9 分 因为sin 2sinB A ，所以由正弦定理得 2b a ……..................................10 分 由余弦定理得 2 2 2 2 cos 3c a b ab    ，即 2 2 2 3c a b ab    ……...........11 分 由①②解得： 1a  ， 2b  ……..........................................................12 分 2、（成都七中 2014 届高三上期中考试） ΔABC 中， ， . （1）求证： ; （2）若 a、b、c 分别是角 A、B、C 的对边， ，求 c 和ΔABC 的面积. （1）证明：由 ，得 ……….2 分 由 ，得 , ∴ , ∴ , ∴ , ∴ …………………6 分 （2）解:由（1）得 ，由 ，得 . 由正弦定理得 , 由 得 ，从而 ……10 分 ∴ ………………..12 分 3、（成都高新区 2014 届高三 10 月统一检测） 已知函数 ， ． （Ⅰ）求函数 的最小值和最小正周期； （Ⅱ）设 的内角 、 、 的对边分别为 、 、 ，满足 ， 且 ，求 、 的值. 解 （Ⅰ） ……3 分 则 的最小值是 ， 最小正周期是 ； ……6 分 （Ⅱ） ，则 ， ……7 分 , ,所以 ， 所以 ， ……9 分 因为 ，所以由正弦定理得 ……10 分 由余弦定理得 ，即 ……11 分 由①②解得： ， ……12 分 4、（成都石室中学 2014 届高三上学期期中） 已知 ABC 中，角 A B C、 、 的对边分别为 a b c、 、 ，且有 ( 2 )cos cosa c B b C  。 （1）求角 B 的大小； （2）设向量 8(cos2 1,cos ), (1, )5A A m = n = ，且 m n ，求 tan( )4 A  的值。 ( 2 )cos cosa c B b C  ( 2 sin sin )cos sin cosA C B B C   2 sin cos sin cos sin cos sin( ) sinA B B C C B B C A      sin 0A  2cos 2B  4B   ………………6 分 (2) 8cos2 1 cos 05m n A A      2 4(cos ) cos 05A A   4cos 0 cos 5A A  或者 cos 0 0,A m  当 时， 舍（不舍 扣 2 分） 4cos tan( ) 75 4A A  当 时， ………………12 分 5、（树德中学高 2014 届高三上学期期中） 已知函数 ( ) sin( )f x A x   （其中 0, 2A   ）的图象如图所示． (1) 求函数 ( )f x 的解析式； (2) 设函数 ( ) 4 14g x f x        ，且  lg ( ) 0g x  ， 求 ( )g x 的单调区间． 【解析】 (1)由图象可知 1A  ， 7 4 12 3 4 T      ，T  ，即 2   ，所以 2  ，所 以 ( ) sin(2 )f x x   ， ………………2 分 7 7 7( ) sin(2 ) sin( ) 112 12 6f           ，即sin( ) 16    ， 所以 2 ,6 2 k k Z      ，即 2 ,3 k k Z    ， ………………3 分 又 2   ，所以 3   ，所以 ( ) sin(2 )3f x x   ； ………………4 分 (2)由(1)得， ( ) sin(2 )3f x x   ，所以 ( ) 4 1 4sin 2 1 4sin 2 14 4 3 2 3g x f x x x                                       4sin 2 1 4sin 2 16 6x x                  ． ………………6 分 又由  lg ( ) 0g x  ，得 ( ) 1g x  ， ∴ 4sin 2 1 16x       ，∴ 1sin 2 6 2x      ， ∴ 52 2 2 ,6 6 6k x k k Z         ………………8 分 其中当 2 2 2 ,6 6 2k x k k Z         时，g(x)单调递增，即 ,6k x k k Z     ，∴ g(x)的单调增区间为 , ,6k k k Z      ………10 分 又∵ 当 52 2 2 ,2 6 6k x k k Z         时，g(x)单调递减， 即 ,6 3k x k k Z       ；∴ ( )g x 的单调减区间为 , ,6 3k k k Z       ．…12 分 综上所述， g(x)的单调增区间为 , ,6k k k Z      ； ( )g x 的 单 调 减 区 间 为 , ,6 3k k k Z       ． ………………13 分 6、（成都外国语学校 2014 届高三 11 月月考） 已知函数 ．（1）求 的 值； （2）若对于任意的 ，都有 ，求实 数 的取值范围． 则 c 的取值范围为 3[ , )2  ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ ┄12 分 7、（达州市普通高中 2014 届高三第一次诊断检测） 如图所示，图象为函数 ( ) sin( )f x A x   ( 0, 0,A   | | , )2 x R   的部分图象如图所示 （1）求 )(xf 的解析式． （2）已知 ( ) 3 ( ) ( ),4g x f x f x   且 tan 3,  求 ( )g x 的值。 π[0, ]2x( )f x cc 2 2π( ) cos ( ) sin6f x x x  π( )12f 解 :(1) 由 图 像 知 1A  , ( )2 3 6 2 T       ,∴ T  ∴ 2 2T    又 2 ( ) 06      得 3   ∴ ( ) sin(2 )3f x x   ……………………6 分 (2)∵ ( ) sin(2 )3f x x   ∴ ( ) 3sin[2( ) ] sin(2 )4 3 3g x x x       3sin(2 ) sin(2 )6 3x x     3(sin 2 cos cos2 sin ) sin 2 cos cos2 sin6 6 3 3x x x x       = x2sin2 ……………………………………………10 分 ∵ tan 3  ∴ ( ) 2sin 2 3g    ……………..12 分 8、（德阳中学 2014 届高三“零诊”考试） 已知函数 wxwxwxxf 2cos2 1cossin3)(  ， ,0w x R 且函数 ( )f x 的最小正周期为 (1)求 w 的值和函数 ( )f x 的单调增区间；(2)在 ABC 中， 角 A、B、C 所对的边分别是 a 、b 、c ，又 4( )2 3 5 Af   ， 2b  ， ABC 的面积等于3 ， 求边长 a 的值． 解：（1）因为 )62sin()(  wxxf ………2 分 由 ( )f x 的最小正周期为 ，得 1w ………3 分 2 2 22 6 2k x k k z         即 6 3k x k k z       ………5 分 所以，函数的增区间为 ,6 3k k k z        ………6 分 （2） 4( )2 3 5 Af    0,A  4 3cos , sin5 5A A   ………8 分 1 3sin 3, 2, sin2 5S bc A b A    5c  ………10 分 由余弦定理 2 2 2 2 cos 13a b c bc A    13a  ………12 分 9、（乐山市第一中学 2014 届高三 10 月月考） 已知函数 23 1( ) sin sin2 2 2 xf x x    ( 0  )的最小正周期为  . (Ⅰ)求 的值及函数 ( )f x 的单调递增区间; (Ⅱ)当 [0, ]2x  时,求函数 ( )f x 的取值范围. 解：(Ⅰ) 3 1 cos 1( ) sin2 2 2 xf x x     3 1sin cos2 2x x   sin( )6x   因为 ( )f x 最小正周期为  ,所以 2  所以 ( ) sin(2 )6f x x   . 由 2 2 22 6 2k x k         , k Z ,得 3 6k x k       . 所以函数 ( )f x 的单调递增区间为[ ,3 6k k     ], k Z (Ⅱ)因为 [0, ]2x  ,所以 72 [ , ]6 6 6x     , 所以 1 sin(2 ) 12 6x     所以函数 ( )f x 在[0, ]2  上的取值范围是[ 1 ,12  ] 10、（乐山市第一中学 2014 届高三 10 月月考）某兴趣小组测量电视塔 AE 的高度 H(单位： m），如示意图，垂直放置的标杆 BC 的高度 h =4m，仰角∠ABE= ，∠ADE=  。 （1）该小组已经测得一组 、  的值，tan =1.24，tan  =1.20，请据此算出 H 的值； （2）该小组分析若干测得的数据后，认为适当调整标杆到电视塔的距离 d（单位：m），使  与  之差较大，可以提高测量精确度。若电视塔的实际高度为 125m，试问 d 为多少时， -  最大？ 解：（1）由 H tanAD  得 HAD tan  ，同理： HAB tan ， BD tan h  。 ∵ AD － AB=DB ， 故 得 H H tan tan tan h     ， 解 得 ： tan 4 1.24H 124tan tan 1.24 1.20 h        。因此，算出的电视塔的高度 H 是 124m。 （2）由题设知 ABd  ，得 H H Htan , tan AD DB h h d d       ， 2 H H tan tantan( ) H H H(H )1 tan tan H(H )1 h hd hd d h hd h dd d d                 ∵ ( ) 2 ( )H H hd H H hd    ， （ 当 且 仅 当 ( ) 125 121 55 5d H H h     时，取等号），∴当 55 5d  时， tan( )  最大。 ∵ 0 2     ，则 0 2     ，∴当 55 5d  时， －  最大。 故所求的 d 是55 5 m。 11、（泸州市 2014 届高三第一次教学质量诊断） 在△ABC 中，角 A 、 B 、 C 的对边分别为 a 、 b 、 c ，设 S 为△ABC 的面积，满足 2 2 24 3( )S a b c   ． (Ⅰ)求角 C 的大小； (Ⅱ)若 tan 21 tan A c B b   ，且 8AB BC     ，求 c 的值． 解：(Ⅰ) 1 sin2S ab C ，且 2 2 2 2 cosa b c ab C   .··························································· 2 分 因为 2 2 24 3( )S a b c   ， 所以 14 sin 2 3 cos2 ab C ab C  ，···························································· ··· 3 分 所以 tan 3C  ，················································································ ··· 4 分 因为 0 C   ， 所以 π 3C  ；························································································· 6 分 （Ⅱ）由 tan 21 tan A c B b   得： cos sin sin cos 2 cos sin A B A B c A B b   ， ···································································7 分 即 sin 2 cos sin C c A B b  ，················································································ 8 分 又由正弦定理得 1cos 2A  ，·································································· ··· 9 分 ∴ 60A   ， ∴△ABC 是等边三角形，····································································· ··10 分 ∴ cos120 8AB BC c c       ，································································11 分 所以 4c  .························································································· ··12 分 12、（绵阳市高中 2014 届高三 11 月第一次诊断性考试） 已知函数 （I）求函数 f（x）的定义域及最大值； （II）求使 f（x）≥0 成立的 x 的取值集合。 解：（Ⅰ） cosx≠0 知 x≠kπ，k∈Z， 即函数 f (x)的定义域为{x|x∈R，且 x≠kπ，k∈Z}．………………………3 分 又∵ xxxxxx xxxxxf 2sin2 2cos12cossin2sin2cos )cos(sincossin2)( 2  )2cos2(sin1 xx  )42sin(21  x ， ∴ 21)( max xf ． ……………………………………………………………8 分 （II）由题意得1 2 sin(2 )4 πx  ≥0，即 sin(2 )4 πx  ≤ 2 2 ， 解得 32 4 πkπ  ≤ 2 4 πx  ≤ 92 4 πkπ  ，k∈Z， 整理得 4 πkπ  ≤x≤ kπ π ，k∈Z． 结合 x≠kπ，k∈Z 知满足 f(x)≥0 的 x 的取值集合为 {x| 4 πkπ  ≤x< kπ π ，k∈Z}．………………………………………………12 分 13、（绵阳市高中 2014 届高三 11 月第一次诊断性考试） 安通驾校拟围着一座山修建一条环形训练道路 OASBCD，道路的平面图如图所示（单 位：km），已知曲线 ASB 为函数 的图 象，且最高点为 S（1,2），折线段 AOD 为固定线路，其中 AO＝ 3 ，OD＝4，折线段 BCD 为可变线路， 但为保证驾驶安全，限定∠BCD＝120°。 （I）求 的值； （II）应如何设计，才能使折线段道路 BCD 最长？ 解：（I）由已知 A=2， 且有 3)0sin(2   ，即 2 3sin  ， 由| |< 2  得 3   ． 又∵ 最高点为(1，2)， ∴ ，2)3sin(2   解得 6   ． ∴ )36sin(2   xy ．…………………………………………………………6 分 （II）∵ B 点的横坐标为 3，代入函数解析式得 2sin( 3 )6 3B π πy    =1， ∴ 2)34(1 22 BD ．…………………………………………………8 分 在△BCD 中，设∠CBD=θ，则∠BDC=180º-120º-θ=60º-θ． 由正弦定理有 )60sin(sin120sin   BCCDBD ， ∴ sin3 62CD ， )60sin(3 62 BC ， …………………………………9 分 ∴ )]60sin([sin3 62   CDBC ]sin2 1cos2 3[sin3 62   )3sin(3 62   ． ∴ 当且仅当 6   时，折线段 BCD 最长，最长为 3 62 千米．…………12 分 14、（什邡中学高中 2014 届高三上学期第二次月考） 已知函数 2( ) 3sin cos cosf x x x x    的周期为 2 ，其中 0  ． （Ⅰ）求 的值及函数 ( )f x 的单调递增区间； （Ⅱ）在 ABC 中，设内角 A、B、C 所对边的长分别为 a、b、c，若 3a  ， 2c  ， f(A)= 3 2 ，求 b 的值． 15、（资阳市 2014 届高三上学期第一次诊断性考试） 已知函数 2( ) 2sin( )cos sin cos 3sin3f x x x x x x    （ xR ）. （Ⅰ）求 ( )f x 在[0 ], 内的单调递增区间； （Ⅱ）在 ABC 中，B 为锐角，且 ( ) 3f B  ， 4 3AC  ，D 是 BC 边上一点，AB AD ， 试求 AD DC 的最大值． 【解】（Ⅰ） 21 3( ) 2( sin cos )cos sin cos 3sin2 2f x x x x x x x    2 22sin cos 3(cos sin )x x x x   sin 2 3cos2x x  2sin(2 )3x   .··························2 分 由 2 2 22 3 2k x k         ，得 5 12 12k x k       （ Zk  ）.·····················3 分 取 0k  ，得 5 12 12x    ，又 [0 ]x  , ，则 5[0 ]12x  , ；····································· 4 分 取 1k  ，得 11 17 12 12x   ，又 [0 ]x  , ，则 11[ ]12x   , .·····································5 分 ∴ ( )f x 在[0 ]， 上的单调递增区间是 5[0 ]12 , ， 11[ ]12  , .······································ 6 分 （Ⅱ）由 ( ) 3f B  得 3sin(2 )3 2B   .又 0 2B   ，则 223 3 3B      ，从而 2 3 3B    ，∴ 3B  .···················································································8 分 由 AB AD 知 ABD 是正三角形， AB AD BD  ，∴ AD DC BD DC BC    ， 在 ABC 中，由正弦定理，得 4 3 sinsin 3 BC BAC   ，即 8sinBC BAC  . ∵ D 是 BC 边上一点，∴ 2 3 3BAC    ，∴ 3 sin 12 BAC   ，知 4 3 8BC  . 当 2 6BAC C   ， 时， AD CD 取得最大值 8.················································ 12 分 【另】在 ACD 中，由正弦定理，得 4 3 2sin sin( ) sin3 3 AD DC C C    ，∴ 8sinAD C ， 8sin( )3CD C  ，则 8sin 8sin( )3AD DC C C    3 18(sin cos sin )2 2C C C   [ 3 18( cos sin )2 2C C  8sin( )3C   ．∵ 2 3ADC   ，∴ 0 3C   ， 2 3 3 3C     ， 当 3 2C    ，即 6C  时， AD DC 取得最大值 8.·············································12 分[ 2012-2013 年联考题 （一） 1【云南省昆明一中 2013 届高三新课程第一次摸底测试理】在△ABC 中的内角 A、B、C 所 对的边分别为 a，b，c，若 2 cos , 2 cos ,b c A c b A  则△ABC 的形状为 A．直角三角形 B．锐角三角形 C．等边三角形 D．等腰直角三角形 【答案】C 【 解 析 】 由 正 弦 定 理 得 sin 2sin cos ,sin 2sin cos ,B C A C B A  ， 即 sin( ) 2sin cos sin cos cos sinA C C A A C A C    ，即 sin cos cos sin 0A C A C  ， 所以sin( ) 0,A C A C   ，同理可得 A B ，所以三角形为等边三角形，选 C. 2. 【 云 南 省 昆 明 一 中 2013 届 高 三 新 课 程 第 一 次 摸 底 测 试 理 】 函 数 cos(2 ) [ , ]6 2y x     在区间 的简图是 【答案】B 【解析】将 cos2y x 的图象向左平移 12  个单位得到函数 cos2( ) cos(2 )12 6y x x     的图象，选 B. 3.【云南省昆明一中 2013 届高三新课程第一次摸底测试理】化简 2 sin 4 4sin ( ) tan( )4 4      则 A．sin 2 B． cos2 C．sin D． cos 【答案】A 【解析】 2 24sin ( ) tan( ) 4cos ( ) tan( ) 4cos( )sin( )4 4 4 4 4 4                   2sin( 2 ) 2cos22      ， 所 以 2 sin 4 sin 4 2sin 2 cos2 sin 22cos2 2cos24sin ( ) tan( )4 4               ，选 A. 4.【云南省玉溪一中 2013 届高三第三次月考 理】函数 ]),0[)(26sin(2   xxy 为增 函数的区间是( ) A. ]3,0[  B. ]12 7,12[  C. ]6 5,3[  D. ],6 5[  【答案】C 【 解 析 】 因 为 2sin( 2 ) 2sin(2 )6 6y x x      ， 由 32 2 2 ,2 6 2k x k k Z         ，解得 5 ,3 6k x k k Z       ，即函数的增区 间为 5[ , ]3 6k k k Z     ，所以当 0k  时，增区间为 5[ , ]3 6   ，选 C. 5. 【 云 南 省 玉 溪 一 中 2013 届 高 三 第 四 次 月 考 理 】 已 知 函 数 ( ) 2sin( )f x x   ( 0,0 π)    的图象如图所示，则 等于（ ） A． 1 3 B．1 C． 3 2 D． 2 【答案】C 【解析】由图象可知 15 3 12 2 8 8 8 T      ,所以 3T  ，又 2 3T    ，所以 2 3   ， 选 C. 6.【云南省玉溪一中 2013 届高三第四次月考理】在 ABC 中，若 cos cos cos2 2 2 a b c A B C  ， 则 ABC 的形状是（ ） A．等腰三角形 B．等边三角形 C．直角三角形 D．等腰直角三角形 【答案】B 【 解 析 】 由 正 弦 定 理 可 知 sin cos ,sin cos ,sin cos ,2 2 2 A B CA B C   由 sin 2sin cos cos2 2 2 A A AA   ，因为 cos 02 A  ，所以 1sin 2 2 A  ，因为 0 A   ，所以 0 2 2 A   ，所以 2 6 A  ，即 3A  .同理可得 ,3 3B C   ，所以三角形为等边三角形， 选 B. 7.【云南省玉溪一中 2013 届高三上学期期中考试理】函数 3 ( ) cos( )2 2 6y sin x x     的最大值为 ( ) A. 4 13 B. 4 13 C. 2 13 D. 13 【答案】C 【解析】 3 3 3 1( ) cos( ) cos cos sin2 2 6 2 2 2y sin x x x x x        1= 3 cos sin2x x ,所以函数的最大值为 2 21 1 13 13( 3) ( ) 32 4 4 2      ，选 C. 8.【云南师大附中 2013 届高三高考适应性月考卷（三）理科】对于函数 1 1( ) (sin cos ) | cos sin |2 2f x x x x x    ，下列说法正确的是（ ） A．该函数的值域是 1,1 B．当且仅当 2 2 ( )2k x k k Z     时， ( ) 0f x  C．当且仅当 2 ( )2x k k Z   时，该函数取最大值 1 D．该函数是以 为最小正周期的周期函数 【答案】B 【解析】 sin sin cos( ) cos sin cos x x xf x x x x    ， ＜ ， ， ≥ ，由图象知，函数值域为 21 2      ， ，A 错；当且仅当 π2 π ( )4x k k  Z 时，该函数取得最大值 2 2 ， C 错；最小正周期为 2π ，D 错. 9.【天津市耀华中学 2013 届高三第一次月考理科】在△ABC 中，a，b，c 分别是角 A，B，C 的对边，a= 3 ，b= 2 ，且 1+2cos(B+C)=0，则 BC 边上的高等于 A、 3 -1 B、 3 +1 C、 3-1 2 D、 3+1 2 【答案】D 【解析】由1 2cos( ) 0B C   ，得 11 2cos 0,cos 2A A   ，所以 3A  。有正弦定理 得 sin sin a b A B  ，即 3 2 sinsin 3 B  ，得 2sin 2B  ，因为b a ，所以 B A ，即 4B  。 由余弦定理得 2 2 2 2 cosa b c bc A   得 23 2 2c c   ，即 2 2 1 0c c   ，解得 2 6 2c  ，所以 BC 边上的高为 2 6 2 1 3sin 2 2 2h c B      ，选 D. 10.【天津市耀华中学 2013 届高三第一次月考理科】把函数 = ( )y sin x x R 的图象上所有的 点向左平行移动 3  个单位长度，再把所得图象上所有点的横坐标缩短到原来的 1 2 倍(纵坐标 不变)，得到的图象所表示的函数是 A、 = (2 - ), R3y sin x x  B、 = ( + ), R2 6 xy sin x  C、 = (2 + ), R3y sin x x  D、 2= (2 + ), R3y sin x x  【答案】C 【解析】把函数 = ( )y sin x x R 的图象上所有的点向左平行移动 3  个单位长度,得到函数 sin( )3y x   ，再把所得图象上所有点的横坐标缩短到原来的 1 2 倍(纵坐标不变)，得到函 数 sin(2 )3y x   ，所以选 C. 11.【天津市新华中学 2012 届高三上学期第二次月考理】 把函数 sin(2 )4y x   的图 象向右平移 8  个单位，再把所得图象上各点的横坐标缩短到原来的一半，则所得图象对应 的函数解析式是 A. y=sin（4x+ 8 3 ） B. y=sin（4x+ 8  ） C. y=sin4x D. y=sinx 【答案】C 【 解 析 】 把 函 数 sin(2 )4y x   的 图 象 向 右 平 移 8  个 单 位 ， 得 到 函 数 sin[2( ) ) sin 28 4y x x     ，再把所得图象上各点的横坐标缩短到原来的一半，则所得 图象对应的函数解析式是 sin[2(2 )] sin 4y x x  ，选 C. 12.【天津市天津一中 2013 届高三上学期一月考 理】在∆ABC 中,A,B,C 为内角,且 sin cos sin cosA A B B ,则∆ABC 是 A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等腰或直角三角形 【答案】D 【解析】由 sin cos sin cosA A B B 得 sin 2 sin 2 sin( 2 )A B B   ，所以 2 2A B 或 2 2A B  ，即 A B 或 2A B   ，所以三角形为等腰或直角三角形，选 D. 13.【天津市天津一中 2013 届高三上学期一月考 理】函数 f(x)=sin2x-4sin3xcosx(x∈R)的 最小正周期为 A. 8  B. 4  C. 2  D.π 【答案】C 【解析】 2 2 1( ) sin 2 2sin 2 sin sin 2 (1 2sin ) sin 2 cos2 sin 42f x x x x x x x x x      ,所 以函数的周期为 2 2 4 2T       ，选 C. 14.【天津市天津一中 2013 届高三上学期一月考 理】设函数 sin( )3y x   (x∈R),则 f(x) A.在区间[-π, 2  ]上是减函数 B.在区间 2 7[ , ]3 6   上是增函数 C.在区间[ 8  , 4  ]上是增函数 D.在区间 5[ , ]3 6   上是减函数 【答案】B 【解析】当 2 7 3 6x   时， 2 7 3 3 3 6 3x         ，即 3 3 2x      ，此时函数 sin( )3y x   单调递减，所以 sin( )3y x   在区间 2 7[ , ]3 6   上是增函数，选 B. 15.【山东省烟台市莱州一中 2013 届高三 10 月月考（理）】 tan 和       4tan 是方程 02  qpxx 的两根，则 p、q 之间的关系是 A. 01 qp B. 01 qp C. 01 qp D. 01 qp 【答案】D 【解析】根据根与系数之间的关系可得 tan tan = ,tan tan =4 4p q       （ ） （ ） ，所 以 tan( ) tan4tan( )4 11 tan( ) tan4 p q                 ，即 tan 14 1 p q    ，所以 01 qp ， 选 D. 16. 【 山 东 省 烟 台 市 莱 州 一 中 2013 届 高 三 10 月 月 考 （ 理 ） 】 已 知    ,13 5cos,5 3cos  、  都是锐角，则 cos = A. 65 63 B. 65 33 C. 65 33 D. 65 63 【答案】C 【 解 析 】 因 为 ,  是 锐 角 ， 所 以 0      ， 又   5cos 013      ， 所 以 2       ，所以   12sin 13    ， 4sin 5   . 又 cos cos( ) cos( )cos sin( )sin                5 3 12 4 33 13 5 13 5 65       ， 选 C. 17.【山东省烟台市莱州一中 2013 届高三 10 月月考（理）】如果函数   xy 2cos3 的 图像关于点      0,3 4 中心对称，那么  的最小值为 A. 6  B. 4  C. 3  D. 2  【答案】A 【解析】函数关于点 4( ,0)3  对称，则有 43cos(2 ) 03     ，即 8cos( ) 03    ，所以 2cos( ) 03    ，即 2 2 ,3 2 k k Z      ，即 2 ,6 k k Z     ，所以当 0k  时， 6   ，此时  最小，选 A. 18.【山东省烟台市莱州一中 2013 届高三 10 月月考（理）】函数     bxAxf  sin 的 图象如下，则      201110 fffS  等于 A.0 B.503 C.1006 D.2012 【答案】D 【解析】由图象可知，函数的最大值为 3 2A b  ，最小值为 1 2A b   ，解得 1 , 12A b  ， 函数的周期 4T  ，即 2 4T    ，所以 2   ，所以   1 sin 12 2f x x       ，当 0x  时，   10 sin 1 12f    ，所以sin 0  ，所以 0  ，即   1 sin 12 2f x x  .在一个 周 期 内 (0) (1) (2) (3) 4f f f f    ， 所 以      0 1 2011 503 [ (0) (1) (2) (3)]S f f f f f f f        503 4 2012   ， 选 D. 19.【山东省烟台市莱州一中 20l3 届高三第二次质量检测 （理）】已知 2sin 3   ，则  cos 3 2  等于 A. 5 3  B. 1 9 C. 1 9  D. 5 3 【答案】C 【解析】     2cos 3 2 cos 2 cos2 (1 2sin )             2 4 11 2sin 1 2 9 9          ，选 C. 20.【山东省烟台市莱州一中 20l3 届高三第二次质量检测 （理）】函数    sinf x x   （ 其中 ＞ 0,  ＜ 2  ）的图象如图所示，为了得到   sing x x 的图象，可以将  f x 的 图象 A.向右平移 6  个单位长度 B.向右平移 3  个单位长度 C.向左平移 6  个单位长度 D.向左平移 3  个单位长度 【答案】A 【解析】由图象知 7 4 12 3 4 T      ，所以周期T  ，又 2T    ，所以 2  ，所 以    sin 2f x x   ，又 7 7( ) sin(2 ) 112 12f        ，即 7sin( ) 16     ，所以 7 3 2 ,6 2 k k Z      ，即 2 ,3 k k Z    ，所以当 0k  时， 3   ，所以   sin 2 3f x x      ，又   sin 2 sin[2 ] sin[2( ) ]3 3 6 3g x x x x          ，所以要 得到   sing x x 的图象只需将 ( )f x 的图象向右平移 6  个单位长度，选 A. 21.【山东省烟台市莱州一中 20l3 届高三第二次质量检测 （理）】2009 年北京庆阅兵式上 举行升旗仪式，如图，在坡度为 15°的观礼台上，某一列座位与旗杆在同一个垂直于地面 的平面上，在该列的第一排和最后一排测得旗杆顶端的仰角分别为 60°和 30°，且第一排 和 最 后 一 排 的 距 离 为 10 6 米 ， 则 旗 杆 的 高 度 为 ______ 米 。 【答案】30 【 解 析 】 设 旗 杆 的 高 度 为 x 米 ， 如 图 ， 可 知 0 0180 60 15 105ABC      ， 030 15 45CAB     ， 所 以 180 105 45 30ACB        ，根据正弦定理可知 sin 45 sin30 BC AB  ，即 20 3BC  ， 所以sin 60 20 3 x x BC   ，所以 320 3 302x    米。 22. 【 山 东 省 烟 台 市 莱 州 一 中 2013 届 高 三 10 月 月 考 （ 理 ） 】 若 ,2tan  则  cossin _________. 【答案】 2 5 【解析】 2 2 sin cos sin cossin cos 1 sin cos          2 tan 2 2 1 tan 1 4 5      . 23.【山东省烟台市莱州一中 2013 届高三 10 月月考（理）】关于函数   xxxf 2cos2sin  有下列命题： ①函数  xfy  的周期为 ； ②直线 4 x 是  xfy  的一条对称轴； ③点      0,8  是  xfy  的图象的一个对称中心； ④将  xfy  的图象向左平移 4  个单位，可得到 xy 2sin2 的图象.其中真命题的序号 是______.（把你认为真命题的序号都写上） 【答案】①③ 【解析】   sin 2 cos2 2 sin(2 )4f x x x x     ，所以周期T  ，所以①正确，当 4 x 时 ， 2 sin(2 ) 2 sin4 4 4 4f            不 是 最 值 ， 所 以 ② 不 正 确. 2 sin(2 ) 08 8 4f           ，所以③正确.将  xfy  的图象向左平移 4  个单位， 得到 2 sin[2( ) ] 2 sin(2 )4 4 4y x x       ，所以④不正确，综上正确的命题为①③. 24.【天津市天津一中 2013 届高三上学期一月考 理】已知 3sin cos 8x x  ,且 ( , )4 2x   , 则 cos sinx x  _________. 【答案】 1 2  【 解 析 】 因 为 ( , )4 2x   ， 所 以 sin cosx x ， 即 cos sin 0x x  ， 所 以 2 1(cos sin ) 1 2sin cos 4x x x x    ，所以 1cos sin 2x x   。 25.【天津市天津一中 2013 届高三上学期一月考 理】函数 ( ) sin(2 )3f x x   (x∈R)的图 象为 C,以下结论中: ①图象 C 关于直线 11 12x  对称; ②图象 C 关于点 2( ,0)3  对称; ③函数 f(x)在区间 5( , )12 12   内是增函数; ④由 3sin 2y x 的图象向右平移 3  个单位长度可以得到图象 C. 则正确的是 .(写出所有正确结论的编号) 【答案】①②③ 【解析】当 11 12x  时， 11 11 11 3) sin(2 )=sin( )=sin( )= 112 12 3 6 3 2f          （ ，所以 为 最 小 值 ， 所 以 图 象 C 关 于 直 线 11 12x  对 称 ， 所 以 ① 正 确 。 当 2 3x  时 ， 2 2) sin(2 )=sin =03 3 3f      （ ，所以图象 C 关于点 2( ,0)3  对称;所以②正确。 2 22 2k x k       ， 当 5 12 12x    时 ， 526 6x    ， 所 以 526 3 3 6 3x          ，即 22 3 2x      ，此时函数单调递增，所以③正确。 3sin 2y x 的图象向右平移 3  个单位长度，得到 23sin 2( ) 3sin(2 )3 3y x x     ， 所以④错误，所以正确的是①②③。 26.【天津市新华中学 2012 届高三上学期第二次月考理】在△ABC 中，若 sinA=2sinBcosC 则△ABC 的形状为________。 【答案】等腰三角形 【 解 析 】 在 三 角 形 中 sin sin( ) sin cos cos sinA B C B C B C    ， 即 sin cos cos sin 2sin cosB C B C B C  ，所以sin cos cos sin sin( ) 0B C B C B C    ， 所以 B C ，即三角形为等腰三角形。 27.【天津市耀华中学 2013 届高三第一次月考理科】函数 ( )= ( + )( , ,f x Asin x A    为常数， A>0,  >0) 的 部 分 图 象 如 图 所 示 ， 则 f(0) 的 值 是 ； 【答案】 6 2 【解析】由图象可知 72, 4 12 3 4 TA       ,所以T  ，又 2T    ，所以 2  ， 所以函数 ( )= 2 (2 + )f x sin x  ，由 7 7 7( )= 2 (2 + )= 2 ( + )= 212 12 6f sin sin     ， 得 7( + )= 16sin    ， 所 以 7 3+ = 26 2 k ,k Z    ， 即 = 23 k ,k Z   ， 所 以 ( )= 2 (2 + )3f x sin x  ， 3 6(0)= 2 23 2 2f sin     。 28.【天津市耀华中学 2013 届高三第一次月考理科】在△ABC 中，a，b，c 分别是角 A，B，C 的对边，若 2 2 2+ =2012a b c ，则 ( + ) tan A tan B tanC tan A tan B  的值为 ； 【答案】 2011 2 【解析】 ( + ) sin Asin B tan A tan B cos Acos B sinC sin A sin BtanC tan A tan B cosC cos A cos B    （ ） 2= = sin Asin B sin Asin BcosC sin Asin BcosCcos Acos B sinC sin Acos B cos Asin B sinC sin A B sin C cosC cos Acos B    （ ） 2 2 2 2 2 2 2 2012 2011= 2 2 2 ab a b c c c c ab c      。 29.【云南师大附中 2013 届高三高考适应性月考卷（三）理科】在锐角△ABC 中，角 A、B、 C 所对的边分别为 a、b、c，若 b=2，B= 3  且 sin2A+sin(A+C)=sinB，则△ABC 的面积 为 。 【答案】 3 【解析】 sin 2 sin sin( ) 2sin cos sin( ) sin( )A B A C A A A C A C        ， ， 2sin cos 2cos sin . cos 0 π 1 3sin sin 2 2 3.3 2 2ABC A A A C ABC A A C A C B S                 △ △ 是锐角三角形， ， ，即 ， 30【山东省临沂市 2013 届高三上学期期中考试理】在△ABC 中，若 1cos ,3A  则 2sin cos22 B C A  的值为 . 【答案】 1 9  【解析】 2 2sin cos2 sin cos22 2 B C AA A    2 21 coscos cos2 2cos 12 2 A AA A     , 因为 1cos ,3A  所以 2 1sin cos22 9 B C A    31.【 北京四中 2013 届高三上学期期中测验数学（理）】已知函数 ，给 出下列四个说法： ①若 ，则 ； ② 的最小正周期是 ； ③ 在区间 上是增函数； ④ 的图象关于直线 对称． 其中正确说法的序号是______. 【答案】③④ 【解析】函数 1( ) sin cos sin 22f x x x x  ，若 1 2( )= ( )f x f x ，即 1 2 1 1sin 2 = sin 22 2x x ， 所 以 1 2sin 2 = sin 2x x ， 即 1 2sin 2 =sin( 2 )x x ， 所 以 1 22 = 2 2x x k  或 1 22 = 2 2 ,x x k k Z    ，所以①错误； 2,  所以周期 2T    ，所以②错误；当 4 4x    时 ， 22 2x    ， 函 数 递 增 ， 所 以 ③ 正 确 ； 当 3 4x  时 ， 3 1 3 1 3 1( ) sin 2 )= sin =4 2 4 2 2 2f     （ 为最小值，所以④正确，所以正确的有 2 个. 32.【 北京四中 2013 届高三上学期期中测验数学（理）】定义一种运算 ， 令 ，且 ， 则函数 的最大值是______. 【答案】 5 4 【解析】令 ，则 ∴由运算定义可知， ∴当 1sin 2x  ，即 6x  时，该函数取得最大值 5 4 . 由图象变换可知， 所求函数 的最大值与函数 在区间 上的最大值相同. 33. 【 山 东 省 德 州 市 乐 陵 一 中 2013 届 高 三 10 月 月 考 数 学 理 】 若 α 是 锐 角 ， 且 1sin( ) , cos6 3    则 的值是 . 【答案】 2 6 1 6  【 解 析 】 ∵  是 锐 角 ，  0 2   , 6 6 3       , 所 以 2 2 2cos( ) 1 sin ( )6 6 3        ， cos cos[( ) ] cos( )cos sin( )sin6 6 6 6 6 6                2 2 3 1 1 2 6 1 3 2 3 2 6      . 34. 【 山 东 省 德 州 市 乐 陵 一 中 2013 届 高 三 10 月 月 考 数 学 理 】 函 数 ( ) sin( )( 0, 0)f x A x A      的 图 象 如 图 所 示 ， 则 (1) (2) (3) (2011)f f f f    的值等于 【答案】 2( 2 1) 【解析】由图知， 2A  ， 6 2 42 T    ，所以周期 28 , 4T      ，又 (2) 2f  ， 所以 2sin( 2 ) 24     ，所以 sin( ) 12    ，即 2 ,2 2 k k Z      ，所以 2 ,k k Z   ， 所 以 ( ) 2sin( 2 ) 2sin( )4 4f x x k x    ， 又 2 8(1) (2) (8) 2(sin sin sin ) 04 4 4f f f            ， 所 以 (1) (2) (2011) (1) (2) (3) 2( 2 1)f f f f f f        . 35.【山东省实验中学 2013 届高三第一次诊断性测试理】在△ABC 中，角 A，B，C 的对边为 a，b，c，若 3, 2, 45a b B    ，则角 A= 。 【答案】 60 或120 【解析】由正弦定理可知 sin sin a b A B  ，即 3 2 2sin sin 45A   ，所以 3sin 2A  ，因为 a b ，所以 45A   ,所以 60A   或 120A   。 36.【山东省德州市乐陵一中 2013 届高三 10 月月考数学理】如图，测量河对岸的塔高 AB 时， 可 以 选 与 塔 底 B 在 同 一 水 平 面 内 的 两 个 测 点 C 与 D ， 测 得 015 , 30BCD BDC     ,CD=30 ， 并 在 点 C 测 得 塔 顶 A 的 仰 角 为 60. 则 塔 高 AB=__________. 【答案】15 6 【解析】因为 015 , 30BCD BDC     ,所以 135CBD   ，在三角形 BCD 中，根据正 弦定理可知 sin sin CD BC CBD BDC  ,即 0 30 sin135 sin30 BC  ，解得 15 2BC  ，在直角 ABC 中， tan 60 3AB BC   ，所以 3 3 15 2 15 6AB BC    . 37.【山东省聊城市东阿一中 2013 届高三上学期期初考试 】在△ABC 中，若∠A:∠B:∠ C=1:2:3,则 cba :: 【答案】 1 3： ：2 【解析】因为∠A:∠B:∠C=1:2:3,则可知 A,B,C 分别为 0 0 030 ,60 ,90 , ，根据直角三角形中 边的比例关系可知， : : 1: 3 : 2a b c  38. 【 山 东 省 聊 城 市 东 阿 一 中 2013 届 高 三 上 学 期 期 初 考 试 】 已 知   tan)0,2(,3 1)2sin( ，则 【答案】． 22 【解析】因为 1 1 2 2sin( ) , ( ,0)2 3 2 3 3           ，cos ,sin 则 tan 2 2   。 54【山东省临沂市 2013 届高三上学期期中考试理】已知下列四个命题： ①若 4tan 2, sin 2 5   则 ； ②函数 2( ) lg( 1 )f x x x   是奇函数； ③“ a b ”是“ 2 2a b ”的充分不必要条件； ④在△ABC 中，若sin cos sinA B C ，则△ABC 是直角三角形. 其中所有真命题的序号是 . 【答案】①②④ 【 解 析 】 2 2 2 2sin cos 2tan 4sin 2 sin cos 1 tan 5          ， 所 以 ① 正 确 ； 2 2 1( ) lg( 1 ) lg( ) ( ) 1 f x x x f x x x           为奇函数，所以②正确；由 2 2a b 可 知 a b ，所以“ a b ”是“ 2 2a b ”的充要条件，所以③不正确；由sin cos sinA B C 得 sin cos sin( ) sin cos cos sinA B A B A B A B    , 所 以 cos sin 0A B  ， 所 以 cos 0A  ，即 2A  ，所以△ABC 是直角三角形，所以④正确，所以真命题的序号是①② ④. 39. 【 山 东 省 实 验 中 学 2013 届 高 三 第 二 次 诊 断 性 测 试 理 】 在 ABC 中 ， BABA tantan33tantan  ， 且 4 3cossin  AA ， 则 此 三 角 形 为 . 【答案】等边三角形 【 解 析 】 由 BABA tantan33tantan  得 ， tan tan 3 3 tan tanA B A B     ， 所 以 tan tantan( ) 31 tan tan A BA B A B     ， 即 tan( ) 3 tanC C      ， 所 以 tan 3, 3C C   。 由 4 3cossin  AA 得 sin 0,cos 0A A  ， 3sin 2 2A  ，得 2 3A  或 22 3A  ，所以 6A  或 3A  。当 6A  时， 3 6 2B       ，此时 tan B 不存在，不成立，舍去。当 6A  时， 3 3 3B       ，此时 A B C  ，三角形为等边三角形。 40.【山东省师大附中 2013 届高三 12 月第三次模拟检测理】在 ABC 中，sin ,sin ,sinA B C 依次成等比数列，则 B 的取值范围是 【答案】 (0, ]3  【解析】因为sin ,sin ,sinA B C 依次成等比数列，所以 2sin sin sinA C B ，即 2ac b ， 所 以 2 2 2 2 2 2 2 1cos 2 2 2 2 a c b a c ac a cB ac ac ac         ， 所 以 2 2 1 2 1 1cos 2 2 2 2 2 a c acB ac ac      ，所以 0 3B   ，即 B 的取值范围是 (0, ]3  。 41.【山东省烟台市 2013 届高三上学期期中考试理】 在 ABC 中，若sin 2cos cosA B C , 则 tan tanB C  __________. 【答案】2 【解析】在 ABC 中， CBCBCBA sincoscossin)sin(sin  ,coscos2 CB 两 边同除以 cos cosB C 得 tan tan 2B C  . 42.【山东省烟台市 2013 届高三上学期期中考试理】函数 ）（  2,0),3sin(2  xxy 的单 调递增区间为 【答案】 ]6 11 6 5[  ， 【 解 析 】 由 )3sin(2)3sin(2   xxy 知 当  322  xk  k22 3  即 )(26 1126 5 Zkkxk   时， y 为增函数. )2,0( x ,∴函数的增区间为 ]6 11,6 5[  . （二） 1.【山东省泰安市 2013 届高三上学期期中考试数学理】（本小题满分 12 分） 已知函数    22sin cos 2 3sin 3 0f x x x x       ，直线 1 2,x x x x  是函数  y f x 的图像的任意两条对称轴，且 1 2x x 的最小值为 2  . （I）求 的值； （II）求函数  f x 的单调增区间； （III）若   2 3f   ，求 5sin 46      的值. 【答案】 2.【山东省师大附中 2013 届高三 12 月第三次模拟检测理】(本题满分 12 分)设函数   sin cosf x x x  ，         2 'g x f x f x f x      （Ⅰ）求  g x 的周期和最大值 （Ⅱ）求  g x 的单调递增区间 【答案】（1） ，-------------------------------2 分 ----------------------------------4 分 -------------------------------6 分 的周期 ----------------------7 分 -------------------------8 分 （2）由 得 所以 ---------------------10 分 的增区间为 -------------------12 分 3.【山东省师大附中 2013 届高三 12 月第三次模拟检测理】(本题满分 12 分) 在 ABC 中， 0120 ,A  （Ⅰ）若三边长构成公差为 4 的等差数列，求 ABC 的面积 （Ⅱ）已知 AD 是 ABC 的中线，若 2AB AC    ，求| |AD  的最小值 【答案】解：（1） ，设三边为 ，--------------1 分 由余弦定理： ---------------2 分 即 -------------------------3 分 所以 --------------------------------4 分 -----------------6 分 （2） ----------------------7 分 --------------------8 分 因为 ，所以 --------10 分 ----11 分 所以 ----------12 分 4.【山东省师大附中 2013 届高三上学期期中考试数学理】（本题满分 12 分）已知函数   23sin cos cos .f x x x x  （I）求  f x 的最小正周期和单调递增区间； （II）当 0, 2x      时，求函数  f x 的最大值和最小值及相应的 x 的值. 【答案】 5.【山东省师大附中 2013 届高三上学期期中考试数学理】（本题满分 12 分）已知 ABC 的 三内角 A，B，C 所对三边分别为 a，b，c，且 2sin .4 10A     （I）求 tanA 的值； （II）若 ABC 的面积 24, 6S b  ，求 a 的值. 【答案】 6.【山东省师大附中 2013 届高三上学期期中考试数学理】（本题满分 12 分）设函数   sin cos ,f x x x x x R   . （I）当 0x  时，求函数  f x 的单调区间； （II）当  0,2013x  时，求所有极值的和. 【 答 案 】 7.【山东省实验中学 2013 届高三第三次诊断性测试理】（本小题满分 12 分）在 ABC 内， cba ,, 分别为角 A，B，C 所对的边，a,b,c 成等差数列，且 a=2c。 （1）求 Acos 的值；（Ⅱ）若 4 153ABCS ，求 b 的值。 【答案】解：（Ⅰ）因为 a,b,c 成等差数列，所以 a+c=2b， ……………………2 分 又 ca 2 ，可得 cb 2 3 ， …………………………4 分 所以 4 1 2 32 44 9 2cos 2 222222     c ccc bc acbA ，……………………6 分 （Ⅱ）由（Ⅰ） ),0(,4 1cos  AA ，所以 4 15sin A ， ……………………8 分 因为 AbcSS ABCABC sin2 1,4 153   ， 所以 4 153 4 15 2 3 2 1sin2 1 2  cAbcS ABC ，………………………………10 分 得 3,2,42  bcc 即 . …………………………12 分 8.【山东省青岛市 2013 届高三上学期期中考试理】（本小题满分 12 分） 已知向量 2 2(cos sin ,sin )a x x x    ， ( 3,2cos )b x ， 设函数 ( ) ( R)f x a b x    的图象关于直线 2x  对称，其中 为常数，且 (0,1)  . （Ⅰ）求函数 ( )f x 的表达式； （Ⅱ）若将 ( )y f x 图象上各点的横坐标变为原来的 1 6 ，再将所得图象向右平移 3  个单位， 纵坐标不变，得到 ( )y h x 的图象， 若关于 x 的方程 ( ) 0h x k  在区间[0, ]2  上有且只 有一个实数解，求实数 k 的取值范围. 【答案】 由直线 2x  是 ( )y f x 图象的一条对称轴，可得 2sin( ) 23     ， 所以 ( )3 2k k z      ，即 1 ( )6k k z    ． 又 (0,1)  ， k z ，所以 0k  ，故 1 6   . 9.【山东省青岛市 2013 届高三上学期期中考试理】（本小题满分 12 分） 在 ABC 中， cba ,, 分别是角 CBA ,, 的对边，已知 bcacb 23)(3 222  ． （Ⅰ）若 CB cos2sin  ，求 Ctan 的大小； （Ⅱ）若 2a ， ABC 的面积 2 2S ，且 cb  ，求 cb, ． 【答案】 10.【北京市东城区普通校 2013 届高三 12 月联考数学（理）】（本小题满分13分） 已知：在 ABC 中, a 、 b 、 c 分别为角 A 、 B 、 C 所对的边，且角 C 为锐角， 1cos2 4C   （Ⅰ）求 Csin 的值； （Ⅱ）当 2a ， CA sinsin2  时，求b 及 c 的长． 【答案】解：（Ⅰ）解：因为 cos2C=1-2sin2C= 1 4  ，及 20  C 所以 sinC= 10 4 ． ………………………… 4 分 （Ⅱ）解：当 a=2，2sinA=sinC 时，由正弦定理 a c sin A sin C  ，得 c=4 ………7 分 由 cos2C=2cos2C-1= 1 4  ，及 20  C 得 cosC= 6 4 ………………………9 分 由余弦定理 c2=a2+b2-2abcosC，得 b2－ 6 b-12=0 …………………… 12 分 解得 b=2 6 ……………………13 分 11.【北京市东城区普通校 2013 届高三 12 月联考数学（理）】（本小题满分13分） 已 知 ： 函 数 ( ) sin( )( 0,| | )2f x M x M       的 部 分 图 象 如 图 所 示． （Ⅰ）求 函 数 ( )f x 的 解 析 式； （Ⅱ）在△ ABC 中，角 CBA 、、 的 对 边 分 别 是 cba 、、 ，若 (2 )cos cos , ( )2 Aa c B b C f  求 的 取 值 范 围． 【答案】解：（Ⅰ）由图像知 1M ， )(xf 的最小正周期   )612 5(4T ，故 2 …… 2 分 将点 )1,6( 代入 )(xf 的解析式得 1)3sin(  ，又 2||   故 6   所以 )62sin()(  xxf ……………… 5 分 （Ⅱ）由 CbBca coscos)2(  得 CBBCA cossincos)sinsin2  所以 ACBBA sin)sin(cossin2  ……………………8 分 因为 0sin A 所以 2 1cos B 3 B 3 2 CA ………………9 分 )6sin()2(  AAf 3 20  A 6 5 66   A ……………………11 分 1)6sin()2(2 1  AAf ……………………13 分 12.【 北京四中 2013 届高三上学期期中测验数学（理）】（本小题满分 13 分） 如图，在平面直角坐标系 中，以 轴为始边 作两个锐角 ，它们的终边分别与单位圆交于 两点．已知 的横坐标分别为 ． （1）求 的值； （2）求 的值． 【答案】 （Ⅰ）由已知得： ． ∵ 为锐角 ∴ ． ∴ ． ∴ ．--------------------6 分 （Ⅱ）∵ ∴ ． 为锐角， ∴ ， ∴ ． -----------13 分 13.【 北京四中 2013 届高三上学期期中测验数学（理）】（本小题满分 13 分） 已知函数 . （1）求 函数图象的对称轴方程； （2）求 的单调增区间. （3）当 时,求函数 的最大值，最小值. 【答案】 （I） . …3 分 令 . ∴ 函数图象的对称轴方程是 ……5 分 （II） 故 的单调增区间为 …8 分 (III) , …… 10 分 . …… 11 分 当 时,函数 的最大值为 1,最小值为 . … 13 分 14.【 山东省滨州市滨城区一中 2013 届高三 11 月质检数学理】设 ABC 的内角 A、B、C 的对应边分别为 cba 、、 已知 4 1cos,2,1  Cba （1）求 ABC 的边长。 （2）求 )cos( CA  的值 【答案】（1）由余弦定理得： Cabbac cos2222  ————————————2 分 =1+4—2×1×2× 4 1 =4 ∵c>0 ∴c=2———————————————4 分 （2） 16 15 4 11cos1sin 2 22      CC  C0 4 15sin  C ——————————————6 分 由正弦定理得： C c A a sinsin  4 15 2 sin 1  A 即： 8 15sin A解得， ———————————————————8 分 64 49 8 151sin1cos 2 22       AA 在三角形 ABC 中 ba  BA  为锐角A 8 7cos  A ———————————————————10 分 BACACA sinsincoscos)cos(  —————————————11 分 16 11 4 15 8 15 4 1 8 7  ———————————12 分 15.【 山东省滨州市滨城区一中 2013 届高三 11 月质检数学理】（本题满分 12 分）在△ABC 的三个内角 A、B、C 所对的边分别 a、b、c， 2 , 2 sin .3B a c A  设函数 2( ) sin 2 4cos cosf x x A x  （1）求角 C 的大小； （2）求函数 )(xf 的单调递增区间 【答案】解 xAxxf ACC CA CAACA AcaB 2coscos42sin)(2 46,30 ,2 1sin0sin 23,sinsin2sin sin2,3 21      ）（ 分 分 ）（    分5cos2 342sin 2  xx )2 2cos1(322sin xx  = 分732cos32sin  xx 分（ 83)32sin2  x 分令 9,223222  Zkkxk  分111212 5   kxk 分）的增区间为 12,12,12 5(      Zkkkxf  16.【山东省德州市乐陵一中 2013 届高三 10 月月考数学理】(本小题满分 12 分) 已知 .4 7 12 17,5 3)4(cos   xx (1) 求 x2sin 的值. (2)求 x xx tan1 sin22sin 2   的值 【答案】解: (1) ∵ xxx 2sin)22cos()4(2cos   1)4(cos2)4(2cos 2  xx 又 25 7125 92  ∴ 25 72sin x ................................................ 5 分 )4tan(2sintan1 )tan1(2sin tan1 )cos sin1(2sin tan1 sin22sin)2( 2 xxx xx x x xx x xx        w_w w. k#s5_u.c o*m........... 7 分 ∵ .4 7 12 17   x ∴  243 5  x ∴ 5 4)4(cos1)4sin( 2  xx  ............... 10 分 ∴ 3 4)4tan(  x ∴ x xx tan1 sin22sin 2   75 28)3 4(25 7  ........................12 分 17.【山东省德州市乐陵一中 2013 届高三 10 月月考数学理】（本小题满分 12 分） 在 ABC 中，角 CBA ,, 所对的边为 cba ,, 已知 4 10 2sin C . （Ⅰ）求 Ccos 的值； （Ⅱ）若 ABC 的面积为 4 153 ，且 CBA 222 sin16 13sinsin  ，求 cba ,, 的值. 【答案】解：（Ⅰ） 4 1 4 51)4 10(212sin21cos 22  CC ……………………………4 分 （Ⅱ）∵ CBA 222 sin16 13sinsin  ，由正弦定理可得： 222 16 13 cba  由（Ⅰ）可知 4 15cos1sin,0,4 1cos 2  CCCC  . 4 153sin2 1  CabABCS ， 得 ab=6……………………………………………………………………………………8 分 由余弦定理 Cabbac cos2222  可得 316 13 22  cc 4,0,162  ccc ………………………………………………………………………10 分 由                3 2 2 3 6 1322 b a b a ab ba 或得 ， 18.【山东省聊城市东阿一中 2013 届高三上学期期初考试 】（本小题满分 14 分） 已知 (sin ,cos ), ( 3 cos ,cos )a x x b x x  ，设函数 ( ) f x a b  ( )x R （1）求 )(xf 的最小正周期及单调递增区间； （2）当 5[ , ]6 12x    时，求 )(xf 的值域. 【答案】解：（1） 3 1 12 22 2 2( ) sin cosf x x x   12 6 2sin( )x    ∴ )(xf 的最小正周期为 …………4 分 由 2 2 22 6 2k x k         得 3 6 ( )k x k k Z        )(xf 的单调增区间为 3 6[ , ]( )k k k Z      …………8 分 （2）由（1）知 12 6 2( ) sin( )f x x    又当 5 6 12 6 6[ , ] [ , ]x x        ，2 故 1 2 12 6sin( )x     从而 )(xf 的值域为 30 2[ , ] ………14 分 19.【山东省聊城市东阿一中 2013 届高三上学期期初考试 】（本小题满分 12 分）已知函数 2 2 2π( ) cos ( ) sin6f x x x   ． （1）求 π( )12f 的值； （2）若对于任意的 π[0, ]2x ，都有 ( )f x c ，求实数 c 的取值范围． 【答案】解：（1） 2 2π π π π 3( ) cos ( ) sin cos12 12 12 6 2f      ． ……………… 4 分 （2） 1 π 1( ) [1 cos(2 )] (1 cos2 )2 3 2f x x x     1 π 1 3 3[cos(2 ) cos2 ] ( sin 2 cos2 )2 3 2 2 2x x x x     3 πsin(2 )2 3x  ． ………8 分 因为 π[0, ]2x ，所以 π π 4π2 [ , ]3 3 3x   ， 所以当 π π2 3 2x   ，即 π 12x  时， ( )f x 取得最大值 3 2 ． ………………10 分 所以 π[0, ]2x  ， ( )f x c 等价于 3 2 c ． 故当 π[0, ]2x  ， ( )f x c 时， c 的取值范围是 3[ , )2  ． ………………12 分 2.0【山东省聊城市东阿一中 2013 届高三上学期期初考试 】（本小题满分 12 分）在 ABC 中，角 CBA ,, 所对的边为 cba ,, ，已知 4 10 2sin C 。 （1）求 Ccos 的值； （2）若 ABC 的面积为 4 153 ，且 CBA 222 sin16 13sinsin  ，求 cba ,, 的值。 【答案】解：（1） 4 1 4 51)4 10(212sin21cos 22  CC …… 4 分 （2）  CBA 222 sin16 13sinsin  ，由正弦定理可得： 222 16 13 cba  由（1）可知 4 15cos1sin0,4 1cos 2  CCCC  4 153sin2 1  CabS ABC ，得到 6ab …………………………8 分 由余弦定理 Cabbac cos2222  可得 316 13 22  cc 4,0,162  ccc …………………………10 分 由      6 1322 ab ba 可得      2 3 b a 或      3 2 b a ， 所以       4 2 3 c b a 或       4 3 2 c b a ………12 分 2011-2012 年联考题 1、（2012 滨州二模）函数 f（x）＝sin（ x  ）（其中 0,| | 2    ）的图象如图所求， 为了得到 g（x）＝sin x 的图象，可以将 f（x）的图象 （A）向右平移 6  个单位长度 （B）向右平移 3  个单位长度 （C）向左平移 6  个单位长度 （D）向左平移 3  个单位长度 2、（2012 滨州二模）函数 y＝ sin xe （－ x   ）的图象大致为 3、（2012 德州二模）设函数 ( ) sin(2 )3f x x   ，则下列结论正确的是 A．把 ( )f x 的图象向左平移 12  个单位，得到一个偶函数的图象 B． ( )f x 的图象关于点 ( ,0)4  对称 C． ( )f x 的最小正周期为 ，且在[0, ]6  上为增函数 D．f（x）的图象关于直线 x＝ 3  对称 4、（2012 德州一模）已知函数 y Asin( x ) m    的最大值为 4，最小值为 0，两条对 称轴间的最短距离为 2  ,直线 6x  是其图象的一条对称轴，则符合条件的解析式是( ) A. 4 2 6y sin( x )  B． 2 2 26y sin( x )    C. 2 23y sin( x )    D． 2 23y sin( x )   5、（2012 济南 3 月模拟）函数 )2sin(sin xxy   的最小正周期是 A. B.  C. 2π D. 4π 【答案】B 【解析】函数 xxxxxy 2sin2 1cossin)2sin(sin   ，所以周期为 ，选 B. 6、（2012 济南三模）如果若干个函数的图象经过平移后能够重合，则称这些函数为“同簇 函数”. 给出下列函数： ① ( ) sin cosf x x x ； ② ( ) 2sin( )4f x x   ； ③ ( ) sin 3 cosf x x x  ； ④ ( ) 2 sin 2 1f x x  . 其中“同簇函数”的是( ) A．①② B．①④ C．②③ D．③④ 答案：C 解析：若为“同簇函数”，则振幅相同，将函数进行化简① xxxxf 2sin2 1cossin)(  ， ③ ） 3sin(2cos3sin)(  xxxxf ，所以②③振幅相同，所以选 C. 9、（2012 临沂二模）函数 sin( )( 0)y x     的部分图象如图，设 P 是图象的最高点， A B、 是图象与 x 轴的交点，则 tan APB （A）10 （B）8 （C） 8 7 （D） 4 7 【答案】B 【解析】因为函数的平移不改编图象的大小，所以将图图象向右平移   个单位，此时函 数 为 )sin( xy  ， A 点 平 移 到 O 点 ， 因 为 函 数 的 周 期 22   T , 此 时 )0,0(A , )0,2(B , )1,2 1(P , 所 以 )1,2 3(),1,2 1(  PBPA , 4 1)1,2 3()1,2 1(  PBPA ， 所 以 65 1 2 13 2 5 4 1 cos   APB ，所以 65 8sin APB ，即 8 65 1 65 8 tan APB ，选 B. 10、（2012 临沂二模）已知 A 船在灯塔C 北偏东80o 处，且 A 船到灯塔 C 的距离为 2km， B 船在灯塔 C 北偏西 40o 处， A 、 B 两船间的距离为 3km，则 B 船到灯塔 C 的距离为 ____________km。 11、（2012 青岛二模）已知函数 1 π( ) cos , [ , ]2 2 2f x x x x     ， 0 1sin 2x  ， 0 π[ , ]2 2x   ， 那么下面命题中真命题的序号是 ① ( )f x 的最大值为 0( )f x ② ( )f x 的最小值为 0( )f x ③ ( )f x 在 0[ , ]2 x 上是增函数 ④ ( )f x 在 0 π[ , ]2x 上是增函数 A．①③ B．①④ C．②③ D．②④ 【答案】A 【解析】因为 2 1sin 0 x ， ]2,2[0 x ，所以 60 x 。函数的导数为 xxf sin2 1)('  ， 由 0sin2 1)('  xxf ，解得 2 1sin x ，又因为 ]2,2[ x ，所以 62   x ，此时 函数单调递增，由 0sin2 1)('  xxf ，解得 2 1sin x ，又因为 ]2,2[ x ，所以 26   x ，此时函数单调递减，所以①③正确，选 A. 12、（2012 青岛二模）若 tan 2,  则sin cos   . 【答案】 2 5 【解析】 5 2 14 2 1tan tan cossin cossin 222         13、（2012 青岛 3 月模拟）将函数 sin( ) 3 y x   的图象上所有点的横坐标伸长到原来的 2 倍（纵坐标不变），再将所得图象向左平移 3  个单位，则所得函数图象对应的解析式为 A. 1sin( ) 2 3 y x   B. sin(2 ) 6 y x   C. 1sin 2 y x D. 1sin( ) 2 6 y x   14、（2012 日照 5 月模拟）要得到函数 )42cos(3  xy 的图象，可以将函数 xy 2sin3 的图象 （A）沿 x 轴向左平移 8  个单位 （B）沿 x 向右平移 8  个单位 （C）沿 x 轴向左平移 4  个单位 （D）沿 x 向右平移 4  个单位 答案： 解析： .).8(2sin3)42sin(3)]42(2sin[3)42cos(3 Axxxxy 选  15、（2012 泰安一模）函数      xAxf sin （ ,,A 为常数，A＞0， ＞0）的部 分图象如图所示，则      6 f 的值是 ▲ . 16、（2012 烟台二模）已知倾斜角为  的直线 l 与直线 x 2y 2 0   平行，则 tan 2 的值 为 A. 4 5 B. 4 3 C. 3 4 D. 2 3 答案：B 解析：依题意，得： tan ＝ 1 2 ， 2 2tantan 2 1 tan    ＝ 1 11 4  ＝ 4 3 。 17、（2012 烟台二模）函数 y=x+sin x ,  x ,   的大致图象是 答案：C 解析：函数 y 是非奇非偶函数，故排除 B、D；又因为  x ,   时 x＋sin｜x｜≥x 恒成立， 所以，其图象应在 y＝x 的上方。A 错，选 C。 18、（2012 滨州二模）在△ABC 中，内角 A、B、C 的对边分别为 a、b、c，已知 a2+b2=6abcosC， 且 sin2c＝2sinAsinB。 （I）求角 C 的大小； （II）设函数 f（x）＝sin 6x     － cos x ，且 f（x）图象上相邻两最高点间的距 离为 ，求 f（A）的取值范围。 19、（2012 德州二模）在△ABC 中，角 A，B，C 的对边分别是 a、b、c，已知向量 (cos ,cos ), ( ,2 ),m A B n a c b   且 m//n. （I）求角 A 的大小； （II）若 4,a ABC 求 面积的最大值。 解析：（I） 因为 m//n.，所以， cos (2 )cos 0a B c b A   ，由正弦定理，得： sin cos (2sin sin )cos 0A B C B A   ， 所以sin cos 2sin cos sin cos 0A B C A B A   即sin cos sin cos 2sin cosA B B A C A  ， 所以，sin(A+B)＝2sinCcosA 又 A＋B＋C＝ ，所以，sinC＝2sinCcosA，因为 0＜C＜ ，所以 sinC＞0， 所以 cosA＝ 1 2 ，又 0＜A＜ ，所以 A＝ 3  。 （2）由余弦定理，得： 2 2 2 2 cosa b c bc A   ，所以 16＝ 2 2b c bc bc   ，所以 bc≤16， 当且仅当 b＝c＝4 时，上式取“＝“， 所以，△ABC 面积为 S＝ 1 sin2 bc A ≤4 3 ， 所以△ABC 面积的最大值为 4 3 20、（2012 德州一模）已知函数 2 13 2f ( x ) sin xcos x cos x ( x R )    (I)求函数 f ( x )的最小正周期及在区间 π[0, ]2 上的值域； (Ⅱ)在  ABC 中，角 A、B、C 所对的边分别是 a、b、c，又 4 22 3 5 Af ( ) ,b , ABC    的面积等于 3，求边长 a 的值． 21 、 （ 2012 济 南 3 月 模 拟 ） 在 △ ABC 中 ， 角 A,B,C 所 对 的 边 分 别 为 a,b,c, 且 满 足 cos , =3. （1） 求△ABC 的面积； （2） 若 c=1,求 a、sinB 的值. 【答案】解：（1） cosA=2× -1= ,………………………………………………2 分 而 cosA= bc=3，∴bc=5……………………4 分 又 A∈（0，π），∴sinA= ，………………………………………5 分 ∴S= bcsinA= ×5× =2. ………………………………………6 分 （2） ∵bc=5,而 c=1，∴b=5.…………………………………………………8 分 ∴ -2bccosA=20，a= ………………………………10 分 又 ，∴sinB= .……………12 分 22 、（ 2012 济 南 三 模 ） 已 知 函 数 )3cos(sin3)(  xbxaxf 的 图 象 经 过 点 ).0,6 7(),2 1,3(  (1)求实数 ba, 的值； (2)求函数 )(xf 的周期及单调增区间. 23、（2012 莱芜 3 月模拟）已知 ABC 的三个内角 CBA ,, 所对的边分别为 a，b，c，向量 ( , )m a c b a   ， ( , )n a c b  ,且 nm  . (Ⅰ)求角C 的大小; (Ⅱ)若向量 )2cos2,(cos),1,0( 2 BAts  ,试求 ts  的取值范围. 解：(Ⅰ)由题意得 2 2 2( , ) ( , ) 0m n a c b a a c b a c b ab            ，…2 分 即 abbac  222 . ……3 分. 由余弦定理得 2 1 2cos 222  ab cbaC , 3,0   CC . ……………………5 分 24 、 （ 2012 青 岛 二 模 ） 已 知 向 量 )cos,(sin),sin3,(sin xxnxxm  ， 设 函 数 nmxf )( ,若函数 )(xg 的图象与 )(xf 的图象关于坐标原点对称. （Ⅰ）求函数 )(xg 在区间     6,4  上的最大值,并求出此时 x 的值； （Ⅱ）在 ABC 中， cba ,, 分别是角 CBA ,, 的对边， A 为锐角,若 2 3)()(  AgAf ， 7 cb ， ABC 的面积为 32 ，求边 a 的长． 解：（Ⅰ）由题意得： 2 1 cos2 3( ) sin 3sin cos sin 22 2 xf x x x x x    1 sin(2 )2 6x    ………………………………………………………2 分 所以 )62sin(2 1)(  xxg ………………………………………………3 分 因为     6,4 x ，所以     6,3 2 62 x 所以当 262  x 即 6 x 时，函数 )(xg 在区间     6,4  上的最大值为 2 1 . ……………………………………………6 分 25、（2012 青岛 3 月模拟）已知锐角 ABC 中内角 A 、 B 、C 的对边分别为 a 、b 、 c ， 2 2 6 cosa b ab C  ，且 2sin 2sin sinC A B . （Ⅰ）求角C 的值； （Ⅱ）设函数 ( ) sin( ) cos ( 0)6f x x x      ， ( )f x且 图象上相邻两最高点间的距离 为 ，求 ( )f A 的取值范围. 解：（Ⅰ）因为 Cabba cos622  ,由余弦定理知 Cabcba cos2222  所以 ab cC 4cos 2  . 又因为 BAC sinsin2sin 2  ,则由正弦定理得: abc 22  , 所以 2 1 4 2 4cos 2  ab ab ab cC , 所以 3 C . （Ⅱ） 3 3( ) sin( ) cos sin cos 3sin( )6 2 2 3f x x x x x x            由已知 2,2    ,则 ( ) 3sin(2 ),3f A A   因为 3C  , 2 3B A  ,由于 0 ,02 2A B     , 所以 6 2A   , 20 2 3 3A     . 根据正弦函数图象,所以 0 ( ) 3f A  . 26 、 （ 2012 日 照 5 月 模 拟 ） 已 知 函 数 ),0(1)3cos()3cos(sin3)( Rxxxxxf   ，且函数 )(xf 的最小正 周期为 。 （Ⅰ）求函数 )(xf 的解析式； （Ⅱ）在 ABC 中，角 A，B，C 所对的边分别为 cba ,, ，若 ,1)( Bf 3 3BA BC 2    ， 且 4 ca ，试求 2b 的值。 27、（2012 威海二模）已知函数 2 3( ) sin cos 3 cos 2f x x x x      （ 0 ）， 直线 1xx  ， 2xx  是 )(xfy  图象的任意两条对称轴，且 || 21 xx  的最小值为 4  ． （I）求 ( )f x 的表达式； （Ⅱ）将函数 ( )f x 的图象向右平移 8  个单位后，再将得到的图象上各点的横坐标伸长为 原来的 2 倍，纵坐标不变，得到函数 ( )y g x 的图象，若关于 x 的方程 ( ) 0g x k  ，在区 间 0, 2      上有且只有一个实数解，求实数 k 的取值范围. （Ⅱ）将 ( )f x 的图象向右平移个 8  个单位后，得到 sin(4 )6y x   的图象，再将所得图 象所有点的横坐标伸长到原来的 2 倍，纵坐标不变，得到 sin(2 )6y x   的图象. ( ) sin(2 ).6g x x  所以　 -------------------------9 分 令 2 6x t  ，∵ 0 2x   ,∴ 5 6 6t    ( ) 0g x k  ，在区间 0, 2      上有且只有一个实数解，即函数 ( )y g x 与 y k  在区间 0, 2      上有且只有一个交点，由正弦函数的图像可知 1 1 2 2k    或 1k  ∴ 1 1 2 2k   或 1k   . -------------------12 分 28、（2012 烟台二模） 在 锐 角 三 角 形 ABC 中 ， a 、 b 、 c 分 别 是 角 A 、 B 、 C 的 对 边 ， 向 量    m 2b c,cosC ,n a,cosA ,   且 m//n. （1）求角 A 的大小； （2）求函数 2y 2sin B cos 2B3       的值域. 解析：（I） 因为 m//n.，所以， cos (2 )cos 0a C b c A   ，由正弦定理，得： sin cos (2sin sin )cos 0A C B C A   ， 所以sin cos 2sin cos sin cos 0A C B A C A   即sin cos sin cos 2sin cosA C C A B A  ， 所以，sin(A+C)＝2sinBcosA 又 A＋B＋C＝ ，所以，sinB＝2sinBcosA，因为 0＜C＜ ，所以 sinB＞0， 所以 cosA＝ 1 2 ，又 0＜A＜ ，所以 A＝ 3  。 最新模拟 【江西省新钢中学 2012 届高三第一次考试】设函数 )(|,3sin|3sin)( xfxxxf 则 为 A．周期函数，最小正周期为 2 3  B．周期函数，最小正周期为 3  C．周期函数，最小正周期为 2 D．非周期函数 【答案】A 【解析】： 2sin3 ,sin3 0( ) sin3 | sin3 | 0,sin3 0 x xf x x x x      ，周期不变 【江西省新钢中学 2012 届高三第一次考试】5．E，F 是等腰直角△ABC 斜边 AB 上的三等 分点，则 tan ECF  A． 16 27 B． 2 3 C． 3 3 D． 3 4 【江西省新钢中学 2012 届高三第一次考试】6．若 0 2   ， 02     ， 1cos( )4 3    ， 3cos( )4 2 3    ，则 cos( )2    A． 3 3 B． 3 3  C． 5 3 9 D． 6 9  【答案】 C 【解析】： ( ) ( )2 4 4 2          cos( ) cos[( ) ( )]2 4 4 2           cos( )cos( )4 4 2      sin( )sin( )4 4 2      1 3 2 2 6 3 4 3 5 3 3 3 3 3 9 9       故选 C 【江西省新钢中学 2012 届高三第一次考试】7．如图，在△ ABC 中， D 是边 AC 上的点， 且 ,2 3 , 2AB AD AB BD BC BD   ，则sinC 的值为 A． 3 3 B． 3 6 C． 6 3 D． 6 6 【江西省新钢中学 2012 届高三模拟】12.已知 ,2)4tan(  x 则 x x 2tan tan 的值为__________ 【答案】 4 9 【解析】因为 2 2tan( )4tan 2( )4 1 tan ( )4 x x x          2 2 2 1 2   4 3  ,而 tan(2 )2x  =-cot2x,所以 3tan 2 4x   , 又因为 tan 1tan( ) 24 1 tan xx x     ,所以解得 1tan 3x  ,所以 x x 2tan tan 的值为 4 9 . 【河北衡水中学 2012 届高三模拟】13．在 ABC 中， 60 , 3B AC  ，则 2AB BC 的 最大值为 。 【解析】 0 0120 120A C C A     , 0(0,120 )A , 2 2sinsin sin BC AC BC AA B     02 2sin 2sin(120 ) 3cos sinsin sin AB AC AB C A A AC B         ； 2AB BC   3cos 5sin 28sin( ) 2 7 sin( )A A A A      ，故最大值是 2 7 【2012 唐山市高三模拟统一考试理】 2(sin 22.5 cos22.5 )  的值为（ ） A． 21 2  B． 21 2  C． 2 1 D．2 【答案】 B 【解析】 2(sin 22.5 cos22.5 )  ＝ 2 2 2sin 22.5 2sin 22.5 sin 22.5 cos 22.5 1 sin 45 1 2           【 2012 厦 门 市 高 三 模 拟 质 检 理 】 对 任 意 x 、 y ∈ R ， 恒 有 sinx ＋ cosy ＝ 2sin( 2 4 x y   )cos( 42  yx )，则 sin 24 5cos24 13  等于 A. 4 23  B. 4 23  C. 4 21 D. 4 21 【答案】A 【解析】 由 sinx＋cosy＝2sin( 2 4 x y   )cos( 2 4 x y   )，则 35 42 4 24 513 62 4 24 x y x x y y                  sin13 5 1 3 5 2 3cos [sin cos( )]24 24 2 4 6 4         【 2012 厦 门 市 高 三 质 检 理 】 已 知 函 数 f(x) ＝ Asin(  x6 )(A>0，0< < 2  )的部分图象如图所示， P、Q 分别为该图象的最高点和最低点，点 P 的坐标 为(2，A)，点 R 的坐标为(2，0)。若∠PRQ＝ 3 2 ，则 y＝f(x) 的最大值及 的值分别是 A.2 3 , 6  B. 3 , 3  C. 3 , 6  D. 2 3 , 3  【2012 年石家庄市高中毕业班教学质检 1 理】下列函数中，周期是 ，又是偶函数的是 A．y=sinx B．y=cosx C．y=sin2x D．y=cos2x 【答案】 D 【解析】 周期是 的函数是 y=sin2x 和 y=cos2x，其中 y=cos2x 是偶函数 【2012 武昌区高三年级元月调研理】给出以下 4 个命题： ①函数 4 4sin cosy x x  的最小正周期是 ； ②终边在 y 轴上的角的集合是{ | , }2 k k Z    ； ③把函数 3sin 2 3y x      的图象向右平移 6  个单位得到函数 3sin 2y x 的图象； ④函数 sin 2y x      在区间[0, ] 上是减函数． 其中真命题的个数是 （ ） A．1 B．2 C．3 D．4 【2012 年西安市高三年级第四次质检理】设 ，则函数 的 A.图像关于直线 对称 B.图像关于直线 对称 C.图像关于直线 对称 D.图像关于直线 对称 【答案】C 【解析】展开易得 ( ) 2 sin(2 ) 2 cos24 4f x x x     ，函数在对称轴处取得最大值或 者最小值，代入易得答案 C 正确。 【2012 唐山市高三上学期模拟统一考试理】函数 ( ) 3sin 2 cos2f x x x  （ ） A．在 ( , )3 6    单调递减 B．在 ( , )6 3   单调递增 C．在 ( ,0)6  单调递减 D． ( )f x 在 (0, )6  单调递增 【答案】 D 【解析】 3 1( ) 3sin 2 cos2 2( sin 2 cos2 )2 2f x x x x x    2(sin 2 cos cos2 sin ) 2sin(2 )6 6 6x x x      由 2 2 2 ,2 6 2k x k k Z         ，增区间为[ , ],3 6k k k Z     ∴ ( )f x 在 (0, )6  单调递增。 【山东省日照市 2012 届高三模拟理】（6）函数 )20)(sin()(   ，AxAxf 其中 的图象 如图所示，为了得到 xxg 2sin)(  的图象，则只需将 )(xf 的图象 （A）向右平移 6  个长度单位 （B）向右平移 3  个长度单位 （C）向左平移 6  个长度单位 （D）向左平移 3  个长度单位 【山东实验中学 2012 届高三第一次诊断性考试理】8. 要得到函数 的图 像，只需将函数 的图像 （ ） (A).向左平移 个单位 （B).向右平移 个单位 (C).向左平移 个单位 （D).向右平移 个单位[高&考%资(源#网] 【答案】D 【解析】本题主要考查三角函数的平移．三角函数的平移原则为左加右减上加下减。 解：要得到函数 sin(2 )3y x   ，只需将函数 siny x x  中的 减去   ,即得到 sin 2( )6y x   = sin(2 )3y x   【2012 厦门模拟质检理 7】已知函数 f(x)＝sin(ωx＋ 3  )(ω＞0)，将函数 y=f(x)的图象向右平 移  3 2 个单位长度后，所得图象与原函数图象重合ω最小值等于 A. 3 1 B.3 C.6 D.9 【答案】B 【解析】f(x)＝sin(ωx＋ 3  )(ω＞0) 向右平移  3 2 个单位长度得 ),33 2sin()(   xxf 所以 3,23 2   k ；选 B; 【2012 粤西北九校联考理 4】如图，设 A、B 两点在河的两岸，一测量者在 A 的同侧，在所 在的河岸边选定一点 C，测出 AC 的距离为 50m，∠ACB = 45°，∠CAB = 105°后，就 可以计算出 A、B 两点的距离为( ) 【2012 宁德质检理 3】为了得到函数 sin 2y x 的图象，可将函数 sin(2 )6y x   的 图象 （ ） A．向右平移 6  个单位 B．向左平移 6  个单位 C．向右平移 12  个单位 D．向左平移 12  个单位 【答案】C 【解析】 sin(2 ) sin 2( ) sin 26 12 6y x y x x            ，向右平移 12  个单位 【2012 宁德质检理 8】已知 ABC 的面积为 3 , 3,2 3AC ABC    ，则 ABC 的周长 等于 （ ） A．3 3 B．3 3 B A C C． 2 3 D． 3 3 2 【答案】A 【解析】利用三角形面积公式和余弦定理得： 2 21 3 3 13, ,3 2 ,2 2 2 2b ac a c ac     所 以 acca 3)(3 2  得 3a c  【2012 韶关第一次调研理 4】为了在一条河上建一座桥，施工前在河两岸打上两个桥位桩 ,A B （如图），要测算 ,A B 两点的距离，测量人员在岸边定出基线 BC ，测得 50BC m ， 105 , 45ABC BCA     ，就可以 计算出 ,A B 两点的距离为( ) A．50 2 m B．50 3 m C． 25 2 m D. 25 2 2 m 【答案】A 【解析】在 ABC 中，由正弦定理 0 0 , 50 2sin30 sin 45 BC AB AB  ; 【 2012 海 南 嘉 积 中 学 模 拟 理 13 】 设 a 为 第 一 象 限 的 角 ， 3cos2 5a = - ， 则 )24tan()(  xf ． 【答案】 7 1 【解析】因为 a 为第一象限的角， 3cos2 5a = - ，所以 4 1tan ,tan( 2 )3 4 7       【2012 黑龙江绥化市一模理 3】若 tan 3  ，则 2 sin 2 cos   的值为（ ） A.2 B.3 C.4 D.6 【答案】D 【解析】 2 sin 2 2tancos    =6 【2012 浙江瑞安模拟质检理 5】设  2sin)cos(sin f ，则 )5 1(f 的值为（ ） A． 24 25  B． 12 25  C． 24 25 D． 12 25 【答案】A 【解析】令 ,5 1cossin   平方得 25 242sin  ，所以 25 24)5 1( f 【2012  浙江瑞安模拟质检理 13】函数 sin( )( 0)y x     的部分图象如右图所示， 设 P 是 图 象 的 最 高 点 ， ,A B 是 图 象 与 x 轴 的 交 点 ， 则 tan APB = . 【答案】8 【 解 析 】 8tan,65 65cos,2 13,2 5,2  APBAPBBPAPAB 【答案】①②③ 【解析】因为   sin2 cos2f x a x b x＝ ＋ = )2sin(22  xba ，若   6f x f      对一切 x R 恒成立， 6   ， ),62sin()( 22  xbaxf ① 11 012f      正确； ② 7 12 5f f           正确；③  f x 既不是奇函数也不是偶函数正确；④错误，⑤ 错误。 【2012 延吉市质检理 4】在 ABC 中，若 ,24,34,60  ACBCA 则角 B 的大小 为 （ ） A．30° B．45° C．135° D．45°或 135° 【 2012 浙 江 宁 波 市 模 拟 理 】 若 )2,0(   ， 且 2 1)22sin(cos 2   ， 则 tan  . 【答案】1 【 解 析 】 由 题 2 1)22sin(cos 2   即 2 2 1cos cos2 3cos 1 2       ， 解 得 2 2 1cos sin 2    ，又 )2,0(   ，所以 tan 1  。 【2012安徽省合肥市质检理】已知 3sin( )3 5x   ，则 5cos( )6 x  = （ ） A． 3 5 B． 4 5 C． 3 5  D． 4 5  【答案】C 【解析】 5cos( )6 x  3cos( ) sin( )2 3 3 5x x          ，选 C。 【2012 山东青岛市模拟理】已知 tan( ) 34    ，则 tan 的值为 A． 2 1 B． 2 1 C． 4 1 D． 4 1 【答案】A 【解析】由 tan( ) 34    得 1+ tan 31 tan    ，解得 1tan 2   ，选 A。 【2012 山东青岛市模拟理】已知函数 ( ) cos( )f x A x   ( 0, 0,0 )A       为奇 函数，该函数的部分图象如图所示， EFG 是边长为 2 的等边三角形，则 (1)f 的值为 A． 3 2  B． 6 2  C． 3 D． 3 【答案】D 【 解 析 】 由 题 可 知 3, 4A T  ， 从 而 ,2 2     ，所以 (1) 3 cos 3f    ，选Ｄ。 【2012 吉林市模拟质检理】已知 是第四象限角，且 5 3sin  ，则 tan （ ） A. 4 3 B. 4 3 C. 3 4 D. 3 4 【2012 吉林市模拟质检理】为了得到函数 xxxy 2cos2 1cossin3  的图象，只需将函数 xy 2sin 的图象 A.向左平移 12  个长度单位 B.向右平移 12  个长度单位 C.向左平移 6  个长度单位 D.向右平移 6  个长度单位 【2012广东佛山市质检理】把函数 sin ( )y x x R 的图象上所有的点向左平移 6  个单 位长度，再把所得图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到的图象 所表示的函数为（ ） A． sin(2 ),3y x x  R B． sin(2 ),3y x x  R C． 1sin( ),2 6y x x  R D． 1sin( ),2 6y x x  R 【2012 河南郑州市质检理】函数            xxy 4cos4sin2  图象的一条对称轴是（ ） A． 8 x B. 4 x C. 2 x D. x 【答案】B 【解析】因            xxy 4cos4sin2  22sin 1 cos(2 ) 1 sin 24 2x x x           ， 易知 4 x 是其一条对称轴，选 B。 【2012 北京海淀区模拟理】函数 ( ) sin(2 )( , )f x A x A = + Î R 的部分图象如图所示，那 么 (0)f = （A） 1 2- （B） 1- （C） 3 2- （D） 3- 【答案】B 【解析】由图可知 2A = , 6  = - ,故 (0) 2sin( ) 16f = - = - ，选 B。 【2012 延吉市质检理 12】已知 ( ) sin( )f x A x   , ( ) , ( ) 0f A f   ,   的最小值为 3  ,则正数  ． 【答案】 2 3 【解析】由 ( ) sin( )f x A x   , ( ) , ( ) 0f A f   ,   的最小值为 3  ,，所以周期   2 3 4 T ， 2 3 【2012 金华十校高三上学期模拟联考理】已知 1tan 4 7      ，则 tan = ； 【答案】 3 4  【解析】 1 1tan( ) tan 374 4tan tan( ) 14 4 41 tan( ) tan 1 14 4 7                     【2012 唐山市高三上学期模拟统一考试理】在 ABC 中， 60 , 3,C AB AB   边上的高 为 4 ,3 则 AC+BC= 。 【2012 厦门市高三上学期模拟质检理】函数 f(x)＝sin(x＋ 3  )－ 3 cos(x＋ 3  )，x∈[0,2π] 的单调递减区间是 。 【答案】 3[ , ]2 2   （区间的开闭不影响得分） 【解析】本题主要考查两角和与差的正弦和余弦公式、y＝Asin( x  )的单调性. 属于基 础知识、基本运算的考查. f(x)＝sin(x＋ 3  )－ 3 cos(x＋ 3  ) ＝sinxcos 3  ＋ cosxsin 3  － 3 （cosxcos 3  －sinxsin 3  )＝2 sinx ∴函数 f(x)＝sin(x＋ 3  )－ 3 cos(x＋ 3  )，x∈[0,2π]的单调递减区间是 3[ , ]2 2   【2012 黄冈市高三上学期模拟考试理】已知 ABC 中， 2, 3, 60a b B   ，那么角 A 等于 。 【答案】 45 【解析】由正弦定理， 2 3 2sinsin sin sin sin 60 2 a b AA B A      又 60 45a b A B A       【2012 年石家庄市高中毕业班教学质检 1 理】某城市有一块不规则的绿地如图所示，城建 部门欲在该地上建造一个底座为三角形的环境标志，小李、小王设计的底座形状分别为△ ABC、△ABD，经测量 AD=BD=14，BC=10,AC=16,∠C=∠D． (I)求 AB 的长度； (Ⅱ)若建造环境标志的费用与用地面积成正比，不考虑其他因素， 小李、小王谁的设计使建造费用最低，请说明理由． （Ⅱ）小李的设计符合要求. 理由如下： 1 sin2ABDS AD BD D   1 sin2ABCS AC BC C   因为 AD BD  AC BC …………10 分 所以 ABD ABCS S  由已知建造费用与用地面积成正比，故选择 ABC 建造环境标志费用较低。 即小李的设计符合要求.…………12 分 【2012 厦门市高三上学期模拟质检理】在△ABC 中，a、b、c 分别是三个内角 A、B、C 的 对边，a＝2，sin ,5 5 2 B 且△ABC 的面积为 4 （Ⅰ）求 cosB 的值； （Ⅱ）求边 b、c 的长。 【解析】 【2012 江西师大附中高三模拟理】已知向量 ( 3sin ,1)4 xm  ， 2(cos ,cos )4 4 x xn  ， ( )f x m n    (1)若 ( ) 1f x  ，求 cos( )3x  的值； (2)在 ABC 中，角 A B C、 、 的对边分别是 a b c、 、 ，且满足 1cos 2a C c b  ，求函数 ( )f B 的取值范围. 【解析】 解：（1）   2 3 1 1 13sin cos cos sin cos sin ,4 4 4 2 2 2 2 2 2 6 2 x x x x x xf x m n              而   11, sin .2 6 2 xf x        2 1cos cos2 1 2sin .3 2 6 2 6 2 x xx                          （2） 2 2 21 1cos , ,2 2 2 a b ca C c b a c bab        即 2 2 2 1, cos .2b c a bc A     又  0, , 3A A    又 20 , ,3 6 2 6 2 BB            31, .2f B      【2012 黄冈市高三模拟考试理】已知函数 ( ) sin( )( 0,0 )f x x         为偶函数， 其图象上相邻的两个最低点间的距离为 2 。 （1）求 ( )f x 的解析式； （2）若 1( , ), ( )3 2 3 3a f a      ，求 2sin(2 )3a  的值。 【2012 武昌区高三年级元月调研理】设 ABC 的内角 A、B、C 所对的边分别为 a、b、c， 已知 11, 2,cos 4a b C   ，E 为边 AB 的中点。 （I）求 ABC 的周长； （II）求 ABC 的内切圆的半径与 CAE 的面积． 【解析】 解：（Ⅰ）由余弦定理，得 Cabbac cos2222  =4， 2c ，所以三角形的周长为 5． （Ⅱ）由同角三角函数的基本关系，得 4 15sin C ． 由三角形的面积关系，得  rcbaCabS ABC  2 1sin2 1 ． 所以 4 15212 152 1  r ， 解得内切圆的半径 .10 15r 所以 ABCCAE SS  2 1 = 8 15 ． 【 2012浙 江 宁 波 市 模 拟 理 科 】 已 知 (2cos 2 3sin ,1), (cos , )m x x n x y     ， 满 足 0m n   ． （I）将 y 表示为 x 的函数 ( )f x ，并求 ( )f x 的最小正周期； （II）已知 , ,a b c 分别为 ABC 的三个内角 , ,A B C 对应的边长，若 3)2 A( f ，且 2a  ， 求b c 的取值范围． 【2012 吉林市模拟质检理】在某海岸 A 处，发现北偏东 30 方向，距离 A 处 ）（ 13  n mile 的 B 处有一艘走私船在 A 处北偏西 15 的方向，距离 A 处 6 n mile 的 C 处的缉私船奉命以 35 n mile/h 的速度追截走私船. 此时，走私船正以 5 n mile/h 的速度从 B 处按照北偏东 30 方向逃窜，问缉私船至少经过多长时间可以追上走私船，并指出缉私船航行方向. 【2012江西南昌市调研理】已知向量 =sin2C， 其中A,B,C分别为△ABC的三边a,b,c所对的角. （1）求角C的大小； （2）已知A=75°，c= （cm），求△ABC的面积 A C B 30 15 ·· 【2012 广东佛山市质检理】在△ ABC 中，角 A 、B 、C 的对边分别为 a b c、 、 ，若 60B   ， 且 14 11)cos(  CB . （1）求 Ccos 的值； （2）若 5a ，求△ ABC 的面积. 【解析】（1）∵ 14 11)cos(  CB , ∴ 14 35)(cos1)sin( 2  CBCB …………………3分 ∴  cos cos cos( )cos sin( )sinC B C B B C B B C B         7 1 2 3 14 35 2 1 4 11  ……………6分 （2）由（1）可得 7 34cos1sin 2  CC ………………8分 在△ ABC 中，由正弦定理 A a B b C c sinsinsin  ∴ 8sin sin  A Cac , 5sin  a Abb …………………10分 ∴ 3102 3852 1sin2 1S  Bac . …………………12分 【2012 北京海淀区模拟理】在 ABC 中，角 A ，B ，C 所对的边分别为 a ，b ，c ， 2A B ， 3sin 3B  . （Ⅰ）求 cos A的值； （Ⅱ）若 2b = ，求边 ,a c 的长. 因为 sin sin b a B A= ， 2b = ， 所以 2 3 2 2 3 3 a= . 所以 4 6 3a = . ………………………………………10 分 由 1cos 3A = 可知， (0, )2A Î .过点C 作CD AB^ 于 D . 所以 4 6 6 1 10cos cos 23 3 3 3c a B b A= × + × = ´ + ´ = . ………………………………………13 分 【2012 广东韶关市调研理】已知函数 2( ) 2cos 2 3sin cos 1f x x x x   . （1）求 ( )f x 的周期和单调递增区间； （2）说明 ( )f x 的图象可由 siny x 的图象经过怎样变化得到. 2011 年联考题 题组一 选择题 1．（安徽省百校论坛 2011 届高三第三次联合考试理） 已知 3 3cos( ) , | | , tan2 2 2      且 则 等于 （ ） A． 3 3  B． 3 3 C． 3 D．— 3 答案 D. 2．（浙江省金丽衢十二校 2011 届高三第一次联考文）函数 ( ) sin sin( 60 )f x x x    的最 大值是 （ ） A． 3 B． 3 2 C．2 D．1 答案 A. 3.（山东省莱阳市 2011 届高三上学期期末数学模拟 6 理）已知 )2,2(,3 1sin   ， 则 )2 3sin()sin(   的值是（ ） A、 9 22 B、 9 22 C、 9 1 D、 9 1 答案 B. 4．（湖南省嘉禾一中 2011 届高三上学期 1 月高考押题卷）在区间[ 1,1] 上随机取一个数 ,cos 2 xx  的值介于 0 到 1 2 之间的概率为 （ ） A． 1 3 B． 2  C． 1 2 D． 2 3 答案 D. 5. （湖北省补习学校 2011 届高三联合体大联考试题理） 已知 cos( ) 0,cos( ) 0,2       下列不等式中必成立的是( ) A. tan cot2 2   B. sin cos2 2   C. tan cot2 2   D. sin cos2 2   答案 A. 6．（河南省鹿邑县五校 2011 届高三 12 月联考理）函数 ( ) 3sin 2 3f x x      的图像为 C, 如下结论中正确的是 （ ） A．图像 C 关于直线 6x  对称 B．图像 C 关于点 ,06      对称 C．函数 ( )f x 在区间 5,12 12      内是增函数 D．由 3sin 2y x 的图像向右平移 3  个单位长度可以得到图像 C。 答案 C. 7. （河南省辉县市第一高级中学 2011 届高三 12 月月考理）若 cos 2sin 5,    则 tan  A. 1 2  B.2 C. 1 2 D.-2 答案 B. 8. （北京四中 2011 届高三上学期开学测试理科试题） 已知 ，则 等于（ ） A．7 B． C． D． 答案 C. 9.（福建省三明一中 2011 届高三上学期第三次月考理） 已知函数 )(sincos)( Rxxxxf  ，给出下列四个命题： ①若 ;),()( 2121 xxxfxf  则 ② )(xf 的最小正周期是 2 ； ③ )(xf 在区间 ]4,4[  上是增函数； ④ )(xf 的图象关于直线 4 3x 对称； ⑤当     3,6 x 时， )(xf 的值域为 .4 3,4 3       其中正确的命题为 （ ） A．①②④ B．③④⑤ C．②③ D．③④ 答案 D. 10．（浙江省温州市啸秋中学 2010 学年第一学期高三会考模拟试卷）函数 ( ) sin cosf x x x  的最小值是 A． 1 B． 1 2  C． 1 2 D．1 答案 B. 11.（浙江省嵊州二中 2011 届高三 12 月月考试题文） 函数  2cos sin cosy x x x  的最 大值为 （ ） （A） 2 （B） 2 1 （C） 2 （D） 2 1 答案 B. 12.（山东省日照市 2011 届高三第一次调研考试文）已知 4sin ,sin cos 0,5     则 2sin 的 值为 (A) 25 24 (B) 25 12 (C) 5 4 (D) 25 24 答案 A. 13. （福建省四地六校 2011 届高三上学期第三次联考试题理）已知 2 2     ，且 sin cos ,a   其中  0,1a ，则关于 tan 的值，在以下四个答案中，可能正确的是 （ ） A． 3 B．3 或 1 3 C． 1 3  D． 3 或 1 3  答案 C. 14．（甘肃省甘谷三中 2011 届高三第三次检测试题） tan 690°的值为（ ） Ａ． 3 3  Ｂ． 3 3 Ｃ． 3 Ｄ． 3 答案 A. 15. （甘肃省甘谷三中 2011 届高三第三次检测试题） 若 sin 1 sin 1 sin ( [0, ])2          ，则 tan  （ ） A. 4 3  B. 4 3 C. 0 D. 0 或 4 3  答案 D. 16.（福建省四地六校 2011 届高三上学期第三次联考试题理）给出下面的 3 个命题：（1） 函数 |)32sin(|  xy 的最小正周期是 2  ；（2）函数 )2 3sin(  xy 在区间 )2 3,[  上单调递 增；（3） 4 5x 是函数 )2 52sin(  xy 的图象的一条对称轴. 其中正确命题的个数是（ ） A．0 B．1 C．2 D．3 答案 C. 17.（甘肃省甘谷三中 2011 届高三第三次检测试题） 已知函数 ( ) sin ( 0)f x x       的最小正周期为  ，则该函数的图象（ ） A．关于点 0     ， 对称 B．关于直线 x   对称 C．关于点 0     ， 对称 D．关于直线 x   对称 答案 A. 18 ． （ 山 东 省 莱 阳 市 2011 届 高 三 上 学 期 期 末 数 学 模 拟 6 理 ） 已 知 函 数 sin( )y A x k    ( 0)A  的最大值是 4，最小值是 0，最小正周期是 2  ，直线 3x  是 其图象的一条对称轴，则下面各式中符合条件的解析式是（ ） A． 4sin(4 ) 26y x    B． 2sin(2 ) 23y x    C． 2sin(4 ) 23y x    D． 2sin(4 ) 26y x    答案 D. 19．（吉林省东北师大附中 2011 届高三上学期第三次模底考试理） 已 知 函 数 ( ) sin( )( 0)4f x x x R    ， 的 最 小 正 周 期 为  ， 为 了 得 到 函 数 ( ) cosg x x 的图象，只要将 ( )y f x 的图象 （ ） A． 向左平移 8  个单位长度 B． 向右平移 8  个单位长度 C． 向左平移 4  个单位长度 D． 向右平移 4  个单位长度 答案 A. 20．（湖南省嘉禾一中 2011 届高三上学期 1 月高考押题卷）函数 3 2( )f x ax bx cx d    图 象如右图,则函数 2 2 3 3 cy ax bx   的单调递增区间为（ ） A． ( , 2]  B．[3, ) C．[ 2,3] D． 1[ , )2  答案 B. 21．（湖北省涟源一中、双峰一中 2011 届高三第五次月考理）下列函数中，周期为 ，且 在 4 2       ， 上为减函数的是 （ ） A． sin( )2y x   B． cos(2 )2y x   C． sin(2 )2y x   D． cos( )2y x   答案 C. 22．（湖北省部分重点中学 2011 届高三第二次联考试卷）函数 ( ) 2sin(2 )f x x   的图像 如图所示，      ,则 的值为 （ ） A． 3  B． 6  C． 2 3 3   或 D． 5 6 6   或 答案 A. 23．（黑龙江省佳木斯大学附属中学 2011 届高三上学期期末考试理） 函数 2( ) 2cos sin 2 1f x x x   ，给出下列四个命题 （1）函数在区间 5[ , ]8 8   上是减函数； （2）直线 8 x 是函数图象的一条对称轴； （3）函数 )(xf 的图象可由函数 xy 2sin2 的图象向左平移 4  而得到； （4）若 [0, ]2x  ，则 )(xf 的值域是[0, 2] 其中正确命题的个数是 （ ） A．1 B．2 C．3 D．4 答案 B. 24．（黑龙江省哈九中 2011 届高三期末考试试题理）将函数 3sin2y x 的图像按向量 ( ,1)6a   平移之后所得函数图像的解析式为 （ ） A． 3sin(2 ) 13y x    B． 3sin(2 ) 13y x    C． 3sin 2 16y x       D． 3sin(2 ) 16y x    答案 A. 25.（广西北海二中 2011 届高三 12 月月考试题理） sin(2 )3y x   的图象是 （ ） A.关于原点成中心对称 B.关于 y 轴成轴对称 C.关于点 ,012      成中心对称 D.关于直线 12x  成轴对称 答案 D. 26 ． （ 河 南 省 辉 县 市 第 一 高 级 中 学 2011 届 高 三 12 月 月 考 理 ） 已 知 函 数 )sin()(   xAxf ),0,0(  A 的 部 分 图 象如图所示,则函数 )(xf 的解析式为 A． )42 1sin(2)(  xxf B． )4 3 2 1sin(2)(  xxf C． )42 1sin(2)(  xxf D． )4 3 2 1sin(2)(  xxf 答案 B. 27．（广东省高州市南塘中学 2011 届高三上学期 16 周抽考理） 已知函数 ])1cos[(])1sin[()( xaxaaxf  的最大值为 2，则 )(xf 的最小正周期为 （ ） A． 4  B． 2  C． D． 2 答案 C. 28．（北京龙门育才学校 2011 届高三上学期第三次月考）函数 1)4(cos2 2  xy 是 （ ） A．最小正周期为 的奇函数 B．最小正周期为 的偶函数 C．最小正周期为 2  的奇函数 D．最小正周期为 2  的偶函数 答案 A. 29．（福建省厦门外国语学校 2011 届高三 11 月月考理）函数 2( ) 2cos sin 2 1f x x x   ， 给出下列四个命题 （1）函数在区间 5[ , ]8 8   上是减函数； （2）直线 8 x 是函数图象的一条对称轴； （3）函数 )(xf 的图象可由函数 xy 2sin2 的图象向左平移 4  而得到； （4）若 [0, ]2x  ，则 )(xf 的值域是[0, 2] 其中正确命题的个数是 （ ▲ ） A．1 B．2 C．3 D．4 答案 B. 30.（甘肃省甘谷三中 2011 届高三第三次检测试题） 若△ ABC 的内角 A 满足 3 22sin A ， 则sin cosA A = （ ） A． 3 15 B． 3 15 C． 3 5 D． 3 5 答案 A. 31．（广东省清远市清城区 2011 届高三第一次模拟考试理）函数 )sin()(   xAxf （其 16 题图 中 )2,0  A ）的图象如图所示，为了得到 xxg 2sin)(  的图像，则只要将 )(xf 的图 像（ ） A．向右平移 6  个单位长度 B．向右平移 12  个单位长度 C．向左平移 6  个单位长度 D．向左平移 12  个单位长度 答案 A. 32.（广西北海二中 2011 届高三 12 月月考试题理）函数 xy 2sin 的图象按向 )3,6(  a 平 移后的解析式为 （ ） A 3)62sin(  xy B 3)62sin(  xy C 3)32sin(  xy D 3)32sin(  xy 答案 D. 33 ． （ 河 南 省 焦 作 市 部 分 学 校 2011 届 高 三 上 学 期 期 终 调 研 测 试 理 ） 已 知 函 数 ，下面结论错误的是 A．函数 的最小正周期为 B．函数 是奇函数 C．函数 的图象关于直线 对称 D．函数 在区间 上是减函数 答案 D. 34.（贵州省遵义四中 2011 届高三第四次月考理））函数 )32sin(3)(  xxf 的图象为C ， 以下三个命题中，正确的有（ ）个 ①图象 C 关于直线 对称; ②函数 )(xf 在区间 内是增函数; ③由 xy 2sin3 的图象向右平移 个单位长度可以得到图象C . A.0 B.1 C.2 D.3 答案 C. 35．（河南省长葛第三实验高中 2011 届高三期中考试理） 函数       )3 80(),sin(2 )02(,1  xx xkx y 的图象如下图，则 （ ） A． 6,2 1,2 1  k B． 3,2 1,2 1  k C． 6,2,2 1  k D． 3,2,2  k 答案 A. 填空题 36．（重庆市重庆八中 2011 届高三第四次月考文） 在 ABC 中，如果 sin :A sin :B sinC = 5:6:8 ，则此三角形最大角的余弦值是 ． 答案 37．（重庆市南开中学高 2011 级高三 1 月月考文） 若 3(0, ),cos( ) , sin5        则 。 答案 4 5 ； 38.（山东省日照市 2011 届高三第一次调研考试文）关于函数 ( ) sin 2 cos2f x x x  有下列 命题：①函数 ( )y f x 的周期为 π ； ②直线 π 4x  是 ( )y f x 的一条对称 轴；③点 π( ,0)8 是 ( )y f x 的图象的一个对称中心；④将 ( )y f x 的图象向左平移 π 4 个单位， 可得到 2 sin 2y x 的图象．其中真命题的序号是 .（把你认为真命题的序号都写上） 答案 ①③． 39．（北京龙门育才学校 2011 届高三上学期第三次月考）已知  是第二象限的角， 1tan 2    ，则 cos  __________。 答案 2 5 5  40．（北京四中 2011 届高三上学期开学测试理科试题） 的值域为___________。 答案 41．（北京五中 2011 届高三上学期期中考试试题理）函数 )32cos()62sin()(   xxxf 的最小正周期为 答案 2  42．（福建省安溪梧桐中学 2011 届高三第三次阶段考试理）若 是锐角，且   1sin 6 3    ， 则 cos 的值是 ． 答案 2 6 1 6  43.（福建省四地六校 2011 届高三上学期第三次联考试题理）已知 为第二象限角，且 P （ x, 5 ）为其终边上一点，若 cos = 2 4 x 则 x 的值为 答案 3 44．（甘肃省甘谷三中 2011 届高三第三次检测试题）已知 ,       ,4 3 ，sin(   )=－ ,5 3 ,13 12 4sin        则       4 cos  = 答案 56 65  45．（福建省安溪梧桐中学 2011 届高三第三次阶段考试理）下图展示了一个由角的区间(0, ) 到实数集 R 的映射过程：区间(0, )中的角 始边落在 OA 上,则终边对应半圆弧 AB 上的点 M，如图 1；将半圆弧 AB 围成一个椭圆，使两端点 A、B 恰好重合，如图 2；再将这个椭 圆放在平面直角坐标系中，使其椭圆中心在 y 轴上，点 A 的坐标为( )0,1 ，如图 3 中直线 AM 与 x 轴交于点 ( ),0N n ，则 的象就是 n，记作 nf )( ． 下列说法中正确命题的序号是 .(填出所有正确命题的序号) ① 1 14f      ； ②  f x 是奇函数； ③  f x 是定义域上的单调函数； ④  f x 的图象关于点 )0,2( 对称 ; ⑤  f x 的图象关于 y 轴 对称 答案 ③④ 46．（甘肃省甘谷三中 2011 届高三第三次检测试题） 函数 |)0,0)(sin()(   AxAxf 的图象如图所示， 则          2006321 ffff  的值等于 . 答案 3. 47.（广东省新兴惠能中学 2011 届高三第四次月考理）已知 是第二象限角， 2 2sin  ， 则  )4sin(  答案 0. 简答题 48.（甘肃省甘谷三中 2011 届高三第三次检测试题） (12 分)已知函数 2 π( ) 2sin 3 cos24f x x x      ， π π 4 2x      ， ． （I）求 ( )f x 的最大值和最小值；（II）若不等式 ( ) 2f x m  在 π π 4 2x      ， 上恒成立， 2 0 2 6 x y 求实数 m 的取值范围 答案 (1)3,2;(2)(1,4) 49.（山东省日照市 2011 届高三第一次调研考试文）（本小题满分 12 分） 设函数 π π π( ) cos( ) cos4 3 4 x xf x    ． （Ⅰ）求 ( )f x 的最小正周期； （Ⅱ）求函数 ( 2 )y f x   在[0,2] 上的值域． 答案 解：（Ⅰ） ( )f x = π π π π πcos cos sin sin cos4 3 4 3 4 xx x  = 3 π 1 πsin cos2 4 2 4x x = π πsin( ).4 6x  ………………4 分 故 ( )f x 的最小正周期为 T = 2π π 4 =8. …………………………6 分 (Ⅱ) π π( 2 ) sin[ ( 2 ) ]4 6y f x x       = π π πsin( )2 4 6x   = π πcos( )4 6x  . ………………9 分 0 ≤ x ≤ 2 ， π 6  ≤ π π 4 6x  ≤ 2π 3 ， 1 2  ≤ π πcos( )4 6x  ≤ 3 2 ， 即 3 2  ≤ π πcos( )4 6x - ≤ 1 2 所以函数 ( 2 )y f x   在[0,2]上的值域为 3 1[ , ]2 2  . ………………12 分 50．（重庆市南开中学高 2011 级高三 1 月月考文） （13 分） 已知向量 1(1,cos ), ( sin )4a x b x     （1）当 [0, ]4x  时，若 a b  ，求 x 的值； （2）定义函数 ( ) ( ), , ( )f x a a b x R f x      求 的最小正周期及最大值。 答案 51．（湖南省嘉禾一中 2011 届高三上学期 1 月高考押题卷） 已知函数 ( ) cos(2 ) 2sin( )sin( )3 4 4f x x x x       （Ⅰ）求函数 ( )f x 的最小正周期和图象的对称轴方程 （Ⅱ）求函数 ( )f x 在区间[ , ]12 2   上的值域 答案 解：（1） ( ) cos(2 ) 2sin( )sin( )3 4 4f x x x x       1 3cos 2 sin 2 (sin cos )(sin cos )2 2x x x x x x     2 21 3cos 2 sin 2 sin cos2 2x x x x    1 3cos 2 sin 2 cos 22 2x x x   sin(2 )6x   2 2周期T   ∴ 由 2 ( ), ( )6 2 2 3得 kx k k Z x k Z          ∴函数图象的对称轴方程为 ( )3x k k Z   （2） 5[ , ], 2 [ , ]12 2 6 3 6x x          因为 ( ) sin(2 )6f x x   在区间 [ , ]12 3   上单调递增，在区间 [ , ]3 2   上单调递减， 所以 当 3x  时， ( )f x 取最大值 1 又 3 1( ) ( )12 2 2 2f f      ，当 12x   时， ( )f x 取最小值 3 2  所以 函数 ( )f x 在区间[ , ]12 2   上的值域为 3[ ,1]2  52．（北京龙门育才学校 2011 届高三上学期第三次月考）（理科做）（本小题满分 13 分） 已知向量 a ＝ )6cos,6(sin 22 xx  ， 2 2(sin , cos ),6 6b x x   baxg )( 。 （Ⅰ）求函数 ( )g x 的解析式，并求其单调增区间； （Ⅱ）若集合 }),1()2()(|)({ RxxfxfxfxfM  ，试判断 )(xg 与集合 M 的关 系。 答案 解：（Ⅰ） 4 4( ) sin cos6 6g x x x   )6cos6(sin 22 xx   xxx 3cos)6cos6(sin 22   ， 由 ,,366,,232 ZkkxkZkkxk  得 )(xg 的单调增区间为 ).](36,6[ Zkkk  （Ⅱ） )]3 2 3cos(3[cos)2()(   xxxgxg )3 2sin3sin3 2cos3cos3(cos  xxx  1 3( cos sin )2 3 2 3 x x    )1()1(3cos  xgx ， .)( Mxg  53．（甘肃省天水一中 2011 届高三上学期第三次月考试题理）（１０分）求值（每小题 5 分） （1）. 的值。和，求，，已知  cossin13 5)sin(5 3cos20  （2）已知 1sin cos (0 )5x x x π  ， ， ，求 cot x 的值。 答案 （１０分） （1）解： ，，所以，因为 5 4cos1sin205 3cos 2   ，，因为，所以又因为 013 5)sin(2 3 220   ，所以 13 12)(sin1)cos( 2   。 65 16sin)sin(cos)cos(])cos[(cos   （2）解：由 1sin cos 5x x  ……(1)，所以 1 241 2sin cos 2sin cos25 25x x x x   ， ， 因为 (0 )x π ， ，所以sin 0 cos 0x x ， ， 2 24 49(sin cos ) 1 2sin cos 1 25 25x x x x      ， 所以 7sin cos 5x x  ……(2)，联立(1)(2)解得 4 3sin cos5 5x x  ， ， 所以 cos 3cot sin 4 xx x    。 54.（浙江省嵊州二中 2011 届高三 12 月月考试题文）（本小题满分 14 分）已知 ABC 中的 内角 , ,A B C 的对边分别为 , ,a b c ，定义向量  2sin , 3m B  ， 2cos2 ,2cos 12 Bn B      且 / /m n   ． （Ⅰ）求函数   sin 2 cos cos2 sinf x x B x B  的单调递增区间； （Ⅱ）如果 2b  ，求 ABC 的面积的最大值 答案 解：（Ⅰ） nm  // BBB 2cos3)12cos2(sin2 2  BB 2cos32sin  即 32tan B 又 B 为锐角  ,02  B 3 22  B 3  B   sin 2 cos cos2 sin sin 2 3f x x B x B x        2 2 22 3 2k x k        ∴函数的单调递增区间是 5,12 12k k       ． 7 分 （Ⅱ） 得，由余弦定理 ac bcaBbB 2cos2,3 222   0422  acca 又 acca 222  代入上式得： 4ac （当且仅当 2 ca 时等号成立．） 34 3sin2 1  acBacS ABC （当且仅当 2 ca 时等号成立．） 14 分 55．（山东省莱阳市 2011 届高三上学期期末数学模拟 6 理）(本小题满分 12 分) 已知函数 23 1( ) sin 2 cos2 2f x x x   , ( )x R （I）求函数 ( )f x 的最小值和最小正周期； （II）设 ABC 的内角 , ,A B C 的对边分别为 , ,a b c ，且 3c  ， ( ) 0f C  ，若向量 (1,sin )m Auv 与向量 (2,sin )n Bv 共线，求 ,a b 的值. 答案 解:（I） 3 1 cos2 1( ) sin 22 2 2 xf x x    = sin(2 ) 16x   …………3 分 则 ( )f x 的最小值是-2,最小正周期是 2 2T    . ……………………6 分 （II） ( ) sin(2 ) 1 06f C C     ,则 sin(2 )6C  =1, 0 , 0 2 2C C      , 1126 6 6C      , 2 6C    2  , 3C  , …………………………………………8 分 向量  1,sinm A 与向量  2,sinn B 共线  1 sin 2 sin A B  ， ………………………………………………10 分 由正弦定理得， 1 2 a b  ① 由余弦定理得， 2 2 2 2 cos 3c a b ab    ，即 3= 2 2a b ab  ② 由①②解得 1, 2a b  . ……………………………………………12 分 56.（湖北省补习学校 2011 届高三联合体大联考试题理） (12 分)设 (cos ,1), (sin ,2)a x b x  (1)若 / /a b  ,求 2(sin cos )x x 的值 (2)若 ( ) ( )f x a b a    ,求 ( )f x 在[0, ] 上的递减区间 答案 （1） / / 2cos sin 0 tan 2a b x x x     2 2 2 2 2(sin cos ) sin 2sin cos cos cos (tan 2tan 1)x x x x x x x x x        2 2 1 9(tan 2tan 1)1 tan 5x xx     （2） 2 2 1( ) cos sin cos 1 sin(2 )2 4 2f x x x x x        2 2 22 4 2k x k        3 8 8k x k       k z [0, ]x   令 0,1k  得 ( )f x 在区间[0, ] 上的递减区间是 3 7[0, ],[ , ]8 8    57．（福建省安溪梧桐中学 2011 届高三第三次阶段考试理）（本小题满分 13 分） 设函数 ( ) sin cosf x m x x  ( )x R 的图象经过点 π 2      ，1 ． （Ⅰ）求 ( )y f x 的解析式，并求函数的最小正周期和单调递增区间 （Ⅱ）若 ( ) 2 sin12f A  ，其中 A 是面积为 3 3 2 的锐角 ABC 的内角，且 2AB  ， 求 AC 和 BC 的长． 答案 解：（Ⅰ）函数 ( ) sin cosf x m x x  ( )x R 的图象经过点 π 2      ，1 sin cos 12 2m     1m  ………….2 分 ( ) sin cos 2 sin( )4f x x x x      …………………….4 分 函数的最小正周期 2T  …………………….5 分 由 2 22 4 2k x k        可得 32 24 4 4k x k         ( )y f x 的调递增区间为 3[2 ,2 ]( )4 4k k k Z     ………………7 分 （Ⅱ）因为 ( ) 2 sin12f A  即 ( ) 2 sin 2 sin12 3f A   ∴ sin sin 3A  …………………9 分 ∵ A 是面积为 3 3 2 的锐角 ABC 的内角， 3A  ………………….10 分 1 3sin 32 2ABCS AB AC A    3AC  …………………….12 分 由余弦定理得： 2 2 2 2 cos 7BC AC AB AB AC A      …………………….13 分 58、（福建省三明一中 2011 届高三上学期第三次月考理）(本题满分 13 分) A、B 是直线 )0(1)3cos(2cos2)(0 2   xxxfy 与函数 图像的两个相邻交 点，且 .2|| AB （I）求 的值； （II）在锐角 ABC 中，a，b，c 分别是角 A， B，C 的对边，若 ABCcAf  ,3,2 3)( 的面积为 33 ，求 a 的值. 答案 59.（广东省华附、中山附中 2011 届高三 11 月月考理） （12 分）已知 ( )f x  xxxxxx cossin22sin2 3sin2cos2 3cos  ， （Ⅰ）求函数 )(xf 的最小正周期; (Ⅱ) 当 ,2x       ,求函数 )(xf 的零点. 答案 解：（Ⅰ） xxxf 2sin2cos)(  = )42cos(2 x …………………….4 分 故 T …………………………………………………5 分 （Ⅱ）令 0)( xf ， )24cos(2 x =0，又 ,2x       …… ………….7 分 5 924 4 4x      324 2x    …………………………………………9 分 故 5 8x  函数 )(xf 的零点是 5 8x  ……………. 12 分 60. （ 广 东 省 惠 州 三 中 2011 届 高 三 上 学 期 第 三 次 考 试 理 ） （ 12 分 ） 已 知 函 数 ( ) sin( ) sin( ) cos ( , )6 6f x x x x a a R a        为常数 . (Ⅰ)求函数 ( )f x 的最小正周期； (Ⅱ)若函数 ( )f x 在[- 2  ， 2  ]上的最大值与最小值之和为 3 ，求实数 a 的值. 答案 解：（Ⅰ）∵ ( ) 2sin cos cos6f x x x a   3sin cosx x a   2sin 6x a      ……………………4 分 ∴函数 ( )f x 的最小正周期 2T  ………………………6 分 (Ⅱ)∵ ,2 2x       ，∴ 2 3 6 3x      ∴当 6 3x     ，即 2x   时，  min 32f x f a        ……8 分 当 6 2x    ，即 3x  时，  max 23f x f a      ……10 分 由题意，有 ( 3 ) (2 ) 3a a     ∴ 3 1a   ……12 分 61．（河南省长葛第三实验高中 2011 届高三期中考试理）（本小题满分 12 分） 已知函数 aRaaxxxxf ,(2cos)62sin()62sin()(   为常数）． （1）求函数 )(xf 的最小正周期； （2）求函数 )(xf 的单调递增区间； （3） 若 ]2,0[ x 时， )(xf 的最小值为 2 ，求 a 的值． 答案 ∴当 0x 时 )(xf 取得最小值, 即 2)6sin(2  a , ∴ 1a ． ……………12 分 题组二 一、选择题 1.（成都市玉林中学 2010—2011 学年度）函数 93)( 23  xaxxxf ，已知 )(xf 在 3x 时取得极值，则 a = （A）4 （B）3 （C）5 （D）2 答案 C. 解： 3 2 2( ) 3 9 ( ) 3 2 3f x x ax x f x x ax        由已知 3x   时， ( ) 0 3 9 2 3 3 0 5f x a a          故选 C 2．（成都市玉林中学 2010—2011 学年度）  )3 20cos(  （A） 2 1 （B） 2 3 （C）— 2 1 （D）— 2 3 答案 C. 3. (成都市玉林中学2010—2011学年度）已知定义域为R的函数 ( )f x 在 ),8(  上为减函数， 且 ( 8)y f x  函数为偶函数，则 A． (6) (7)f f B． (6) (9)f f C. (7) (9)f f D. (7) (10)f f 答案 D. 4．(成都市玉林中学 2010—2011 学年度） 2sin 2 3y x      的图象是： （A）关于原点成中心对称 （B）关于 y 轴成轴对称 （C）关于点 ,012      成中心对称 （D）关于直线 12x  成轴对称 答案 D. 解：因为 2sin 2 3y x      若是关于中心对称：则 32 ( )3 6 kx k x k Z        ，故 0, 12x x   ，所以不 关于指定的点成中心对称； 若是关于轴对称：则 2 ( )3 2 2 12 kx k x k Z          0k  时，对称轴为 12x  故选 D 5.（江西省 2011 届高三文）直角梯形 ABCD，如图 1，动点 P 从 B 点出发，由 B→C→D→ A 沿边运动，设动点 P 运动的路程为 x，ΔABP 面积为 ( )f x ，已知 ( )f x 图象如图 2，则Δ ABC 面积为（ ） 图 1 图 2 A．10 B．16 C．18 D．32 答案 B. 6．（江西省 2011 届高三理）若函数 f(x)＝x－ p x ＋p 2 在(1，＋∞)上是增函数，则实数 p 的取 值范围是 A．[－1，＋∞) B．[1，＋∞) C．(－∞，－1] D．(－∞，1] 答案 A. 7．（四川省成都市玉林中学 2011 届高三理） 2sin 2 3y x      的图象是： A.关于原点成中心对称 B.关于 y 轴成轴对称 C.关于点 ,012      成中心对称 D.关于直线 12x  成轴对称 D C P BA x y 0 4 9 14 答案 解：因为 2sin 2 3y x      若是关于中心对称：则 32 ( )3 6 kx k x k Z        ，故 0, 12x x   ，所以不 关于指定的点成中心对称； 若是关于轴对称：则 2 ( )3 2 2 12 kx k x k Z          0k  时，对称轴为 12x  故选 D 8．（浙江省桐乡一中 2011 届高三理）要得到函数 y=cos2x 的图象，只需将函数 y=cos(2x- 3  ) 的图象 （A）向右平移 3  个单位 （B）向左平移 3  个单位 （C）向右平移 6  个单位 （D）向左平移 6  个单位 答案 D. 9.（四川省成都外国语学校 2011 届高三 10 月文）同时具有性质：“①对任意 Rx ， )()( xfxf   恒成立；②图象关于直线 3 x 对称；③在 ]3,6[  上是增函数”的函数可 以是（ ） A. )62sin()(  xxf B. )62sin()(  xxf C. )32cos()(  xxf D. )62cos()(  xxf 答案 B. 10.（四川省成都外国语学校 2011 届高三 10 月文）．已知函数 bxxxf  3)( 的图象在点 A ))1(,1( f 处的切线的斜率为 4，则函数 xbxxg 2cos2sin3)(  的最大值是（ ） A. 1 B. 2 C. 2 D. 3 答案 B. 11．（2011 湖南嘉禾一中） xxxy 2cos3 2sin)2sin(sin   的最大值 和最小正周期分 别是 （ ） A． 2 31 B．2，2π C． 2 ，2πD．1，2π 答案 D. 12．（北京四中 2011 届高三上学期开学测试理科试题）函数 的图象 为 C，则下列论断中，正确论断的个数是（ ） （1）图象 C 关于直线 对称； （2）函数 在区间 内是增函数； （3）由函数 的图象向右平移 个单位长度可以得到图象 C. A．0 B．1 C．2 D．3 答案 C. 13．（北京五中 2011 届高三上学期期中考试试题理）将函数 sin 2y x 的图象向左平移 4  个单位长度，向上平移 1 个单位长度，所得图象对应的函数解析式是( ) )(A 22cosy x )(B cos2y x )(C cos2y x  )(D 22cosy x  答案 A. 14.（福建省安溪梧桐中学 2011 届高三第三次阶段考试理）将函数 )42sin(4)(  xxf 的 图象向右平移 个单位,再将图象上每一点的横坐标缩短到原来的 2 1 倍,所得图象关于直线 4 x 对称,则 的最小正值为 ( ) A.  8 1 B.  8 3 C.  4 3 D.  2 1 答案 B. 15.（福建省惠安荷山中学 2011 届高三第三次月考理科试卷） 在同一直角坐标系中， 3cos( )( [0,2 ])2 2 xy x    的图象和直线 2 1y 的交点个数是（ ） A． 0 B． 1 C． 2 D． 4 答案 C. 16．（福建省惠安荷山中学 2011 届高三第三次月考理科试卷） 函数 2( ) 2cos sin 2 1f x x x   ，给出下列四个命题： （1）函数在区间 5[ , ]8 8   上是减函数； （2）直线 8 x 是函数图象的一条对称轴； （3）函数 )(xf 的图象可由函数 xy 2sin2 的图象向左平移 4  而得到； （4）若 [0, ]2x  ，则 )(xf 的值域是[0, 2] 。 其中正确命题的个数是 （ ） A．1 B．2 C．3 D．4 答案 B. 二、填空题 17．（江苏泰兴市重点中学 2011 届理）函数         63sin2 xxf 的最小正周期 T 答案 2 3  ， 18．（江苏泰兴市重点中学 2011 届理）函数         xxxf 2sinsin3  在 Rx  上的最 小值等于 答案 -2。 19．（江苏泰兴市重点中学 2011 届理）函数   xxxf sin2 在  ,0 上的单调增区间为 答案 { , }3   ， 20．（江苏泰兴市重点中学 2011 届理）已知函数 ( )y f x 是奇函数，当 0x  时， 2( ) ( R)f x x ax a   ， (2) 6f  ，则 a  _________ 答案 5 21．（江苏泰兴市重点中学 2011 届理）设函数 ( )f x 是定义在 R 上以 3 为周期的奇函数， 若 (1) 1f  ， 2 3(2) 1 af a   ，则 a 的取值范围是__________________________． 答案 21 3a   ， 22.（江苏省 2011 届高三理）关于函数 )0(|| 1lg)( 2  xx xxf ，有下列命题 ①其图象关于 y 轴对称； ②当 0x 时， )(xf 是增函数；当 0x 时， )(xf 是减函数； ③ )(xf 的最小值是 2lg ； ④ )(xf 在区间（－1，0）、（2,+∞）上是增函数 ⑤ )(xf 无最大值，也无最小值 其中所有正确结论的序号是 答案 ]2 3,2(  23.（湖南省嘉禾一中 2011 届高三上学期 1 月高考押题卷）函数 ( ) 3sin 2 3 πf x x     的图象 为 C ，如下结论中正确的是_______ （写出所有正确结论的编号） ①图象 C 关于直线 11 12 πx  对称； ②图象 C 关于点 2 03 ，     对称； ③函数 ( )f x 在区间 5 12 12，     内是增函数； ④由 3sin 2y x 的图角向右平移 3  个单位长度可以得到图象 C 答案 ①②③ 24．（四川成都市玉林中学 2010—2011 学年度）已知函数 )(|2|)( 2 Rxbaxxxf  ．给 出下列命题：① )(xf 必是偶函数；②当 )2()0( ff  时， )(xf 的图像必关于直线 x＝1 对 称；③若 02 ba ，则 )(xf 在区间[ , ]a   上是增函数；④ )(xf 有最大值 || 2 ba  ． 其 中正确的序号是 。 答案 ③ 解：①不恒为偶函数； ② 2 2 2(0) (2) | | | 4 4 | (4 4 ) 2 (4 4 )f f b a b b a b a b           ， 所以 1 2 2a b a  或 ，若 2( ) | 2 | ( )f x x x b x R     关于 1x  对称， 若 2( ) | 2 2 2 |f x x ax a     不恒关于 1x  对称； ③ 02 ba 时，整个图象在 x 轴的上方（或顶点在 x 轴上） 2 2( ) | 2 | 2f x x ax b x ax b      ，故 )(xf 在区间[ , ]a   上是增函数； ④无最大值。（开口向上） 25．（成都市玉林中学 2010—2011 学年度）已知函数 )(|2|)( 2 Rxbaxxxf  ．给出 下列命题：① )(xf 必是偶函数；②当 )2()0( ff  时， )(xf 的图像必关于直线 x＝1 对称； ③若 02 ba ，则 )(xf 在区间[ , ]a   上是增函数；④ )(xf 有最大值 || 2 ba  ． 其中 正确的序号是 。 答案 ③ 解：①不恒为偶函数； ② 2 2 2(0) (2) | | | 4 4 | (4 4 ) 2 (4 4 )f f b a b b a b a b           ， 所以 1 2 2a b a  或 ，若 2( ) | 2 | ( )f x x x b x R     关于 1x  对称， 若 2( ) | 2 2 2 |f x x ax a     不恒关于 1x  对称； ③ 02 ba 时，整个图象在 x 轴的上方（或顶点在 x 轴上） 2 2( ) | 2 | 2f x x ax b x ax b      ，故 )(xf 在区间[ , ]a   上是增函数； ④无最大值。（开口向上） 三、简答题 26．（江苏泰兴市重点中学 2011 届理）（本小题满分 14 分）：已知函数 bx axxf   21)(  0a 是奇函数，并且函数 )(xf 的图像经过点（1，3），（1）求实数 ba, 的值；（2）求函数 )(xf 的值域 答案 解：（1）函数 bx axxf   21)( 是奇函数，则 )()( xfxf    0,,0,11 22    bbxbxabx ax bx xa  ………（3 分） 又函数 )(xf 的图像经过点（1，3）， ,0,31 1,3)1(   bb af  ∴a=2 ……（6 分） （2）由（1）知  01221)( 2  xxxx xxf ………（7 分） 当 0x 时， ,2212212  xxxx 当且仅当 ,12 xx  即 2 2x 时取等号…（10 分） 当 0x 时，     2212,2212212  xxxxxx 当且仅当 ,1)2( xx  即 2 2x 时取等号……………（13 分） 综上可知函数 )(xf 的值域为     ,2222, …………（12 分） 27．（江苏泰兴市重点中学 2011 届）（14 分）已知    ,0,sin,3 1,cos,1      xxbxa （1）若 ba // ，求 xx xx cossin cossin   的值； （2）若 ba  ，求 xx cossin  的值。 答案（本题满分 14 分） 解：（1） 1 1/ / sin cos tan2 3a b x x x    …………3 分 1 1sin cos tan 1 3 21sin cos tan 1 13 x x x x x x         …………6 分 （2） 1 1sin cos 0 sin cos3 3a b x x x x       …………8 分 2 5(sin cos ) 1 2sin cos 3x x x x     …………10 分 又 (0, ) sin cos 0 ( , ) sin cos 02x x x x x x        且 ……12 分 15sin cos 3x x   ………………14 分 28．（2011 湖南嘉禾一中）（本小题满分 12 分） 已知函数 axxxxf  cos)6sin()6sin()(  的最大值为 1． （1）求常数 a 的值； （2）求 )(xf 的单调递增区间； （3）求 )(xf ≥ 0 成立的 x 的取值集合． 答案 （1） axxxf  cos6cossin2)(  axaxx  )6sin(2cossin3  当 ,1)6sin( 时 x .1,12)( max  aaxf 所以 ……………………4 分 （2）令 ,,22622 Zkkxk   ………………6 分 解得： Zkkxk  ,323 22  所以， )(xf 的单调递增区间是 .],32,3 22[ Zkkk   …………8 分 （3）由 2 1)6sin(0)(  xxf 得 ，……………………10 分 所以， ,,6 52662 Zklxk   解得： Zkkxk  ,3 222  所以， xxf 成立的0)(  的取值集合 },3 222|{ Zkkxkx   ……12 分 29．（2011 湖南嘉禾一中）（本题满分 13 分） 已知函数 )(,1)( 23 Raaxxxf  （1）若在 )(xf 的图象上横坐标为 3 2 的点处存在垂直于 y 轴的切线，求 a 的值； （2）若 )(xf 在区间（-2，3）内有两个不同的极值点，求 a 取值范围； （3）在（1）的条件下，是否存在实数 m，使得函数 1)2(5)( 234  xmxxxg 的 图象与函数 )(xf 的图象恰有三个交点，若存在，试出实数 m 的值；若不存在，说明理由． 答案 解：（1）依题意， ,0)3 2( f ,23)( 2 axxxf  ,03 22)3 2(3 2  a 1a …………………………3 分 （2）若 )(xf 在区间（—2，3）内有两个不同的极值点， 则方程 0)(  xf 在区间（—2，3）内有两个不同的实根， 02 93,332,0)3(,0)2(,0  aaaff 且解得 但 a=0 时， 1)( 3  xxf 无极值点， ∴a 的取值范围为 )2 9,0()0,3(  ……………………8 分 （3）在（1）的条件下，a=1，要使函数 1)2(5)()( 234  xmxxxgxf 与 的图象 恰有三个交点，等价于方程 1)2(51 23423  xmxxxx ， 即方程 0)14( 22  mxxx 恰有三个不同的实根。 x =0 是一个根， 应使方程 0142  mxx 有两个非零的不等实根， 由 1,3,01,0)1(416  mmmm 解得 ………………12 分  存在 1)2(5)()(),,1()1,3( 234  xmxxxgxfm 与使函数 的图象恰 有三个交点…………………………13 分 30．（成都市玉林中学 2010—2011 学年度）（本题满分 12 分）已知向量 a (cos ,2cos )x x ， b  (2cos ,sin )x x  ，若 ( ) a b+1f x   ．（I）求函数 )(xf 的解析式和最小正周期； (II) 若     2,0 x ，求 )(xf 的最大值和最小值． 答案 解：（I）∵a (cos ,2cos )x x , b  (2cos ,sin )x x  , ∴ ( )f x  a ·b+1 22cos 2cos sin( ) 1x x x    ----------------2 分 1cossin22cos1  xxx ---------------------------------4 分 22sin2cos  xx --------------------------------------6 分 2)42sin(2  x ． -------------------------------------------7 分 ∴函数 ( )f x 的最小正周期   2 2T ． --------------------------8 分 (II)     2,0 x ， ∴ 52 ,4 4 4x        ． ------------------------------------------------9 分 ∴ 时即当 8,242   xx ， ( ) 2 2f x 有最大值 ；------------------11 分 时即当 2,4 5 42   xx ， ( )f x 有最小值1-----------------------12 分 31．（四川成都市玉林中学 2010—2011 学年度）（本题满分 12 分）已知向量 a (cos ,2cos )x x ， b  (2cos ,sin )x x  ，若 ( ) a b+1f x   ．（I）求函数 )(xf 的解析式和最小正周期； (II) 若     2,0 x ，求 )(xf 的最大值和最小值． 答案 解：（I）∵a (cos ,2cos )x x , b  (2cos ,sin )x x  , ∴ ( )f x  a ·b+1 22cos 2cos sin( ) 1x x x    ----------------2 分 1cossin22cos1  xxx ---------------------------------4 分 22sin2cos  xx --------------------------------------6 分 2)42sin(2  x ． -------------------------------------------7 分 ∴函数 ( )f x 的最小正周期   2 2T ． --------------------------8 分 (II)     2,0 x ， ∴ 52 ,4 4 4x        ． ------------------------------------------------9 分 ∴ 时即当 8,242   xx ， ( ) 2 2f x 有最大值 ；------------------11 分 时即当 2,4 5 42   xx ， ( )f x 有最小值1-----------------------12 分 32．（四川成都市玉林中学 2010—2011 学年度）（本题满分 14 分）已知二次函数 2( )f x ax bx c   和一次函数 ( )g x bx  ， 其中 , ,a b c R 且 满 足 0)1(,  fcba . （1）证明：函数 )()( xgxf 与 的图象交于不同的两点 A，B； （2）若函数 ]3,2[)()()( 在xgxfxF  上的最小值为 9，最大值为 21，试求 ba, 的值； （3）求线段 AB 在 x 轴上的射影 A1B1 的长的取值范围. 答案 33.（1）由 0)1(,02)()( 22  cbafcbxaxcbxaxxfbxxg 得与 ， ,04,0,0, 2  acbcacba 从而 即函数 )()( xgxf 与 的图象交于不同 的两点 A，B； … … 3 分 （ 2 ） , , , 2 , 2,bc a b a b c a c a b a b a             即 得 已知函数 2( ) 2F x ax bx c   的对称轴为 bx a   ， 故 ( )y F x 在[2，3]上为增函数， ……………6 分 ;1,2,2158)3(,933)2(  babaFbaF 解得 ……8 分 （3）设方程         a cxx a bxx xxcbxaxxF 21 21 21 2 2 ,,02)( 得的两根为 2 2 2 1 1 1 2 1 2 1 2 1 3| | | | ( ) 4 4[( ) ],2 4 cA B x x x x x x a         ……9 分 1, , , ( 2, ),2 ca b c b a c a a c c a            由 得 ……10 分 设 ],4 3)2 1[(4)(|| 22 11  a c a chBA 的对称轴为 )2 1,2()(,2 1  a c a chx 在 上是减函 数， ).32,3(||),12,3(|| 11 2 11  BABA 得 ……12 分 34．（江苏泰兴市重点中学 2011 届）（14 分）设 ABC 的内角 A、B、C 的对边长分别为 a、b、c,且 3 2b +3 2c -3 2a =4 2 bc ． （Ⅰ） 求 sinA 的值； （Ⅱ）求 2sin( )sin( )4 4 1 cos2 A B C A      的值． 答案 解：（Ⅰ）由余弦定理得 2 2 2 2 2cos 2 3 b c aA bc    又 2 10 , sin 1 cos 3A A A    故 （Ⅱ）原式 2sin( )sin( )4 4 1 cos2 A A A       2 2sin( )sin( )4 4 2sin A A A     2 2 2 2 22( sin cos )( sin cos )2 2 2 2 2sin A A A A A    2 2 2 sin cos 2sin A A A  7 .2   35．（江苏泰兴市重点中学 2011 届）（16 分）已知函数 3 2( )f x ax x bx   （其中常数 ,a b R ）， ( ) ( ) ( )g x f x f x  是奇函数。 （1）求 ( )f x 的表达式； （2）讨论 ( )g x 的单调性，并求 ( )g x 在区间 1,2 上的最大值和最小值。 答案 解：（Ⅰ）由题意得 2( ) 3 2f x ax x b    因此 2 2( ) ( ) ( ) (3 1) ( 2)g x f x f x ax a x b x b        因为函数 ( )g x 是奇函数，所以 ( ) ( )g x g x   ，即对任意实数 x ，有 3 2 3 2( ) (3 1)( ) ( 2)( ) [ (3 1) ( 2) ]a x a x b x b ax a x b x b               从而3 1 0, 0a b   ， 解得 1 , 03a b   ，因此 ( )f x 的解析表达式为 2 21( ) .3f x x x   （Ⅱ）由（Ⅰ）知 21( ) 23g x x x   ， 所以 2( ) 2,g x x    令g (x)=0 解得 1 22, 2x x   则当 2 2x   或x> 时， ( ) 0g x  从而 ( )g x 在区间 ( , 2]  ，[ 2, ) 上是减函数， 当 2 2 , ( ) 0x g x   时 ， 从而 ( )g x 在区间[ 2, 2] 上是增函数， 由前面讨论知， ( )g x 在区间[1，2]上的最大值与最小值只能在 1, 2,2x  时取得， 而 5 4 2 4(1) , ( 2) , (2)3 3 3g g g   ， 因 此 ( )g x 在 区 间 [1 ， 2] 上 的 最 大 值 为 4 2(2) 3g  ，最小值为 4(2) .3g  36．（江苏泰兴市重点中学 2011 届理）（本题满分 16 分）设二次函数 2( )f x ax bx c   在区间 2,2 上的最大值、最小值分别是 M、m，集合  | ( )A x f x x  ． （1）若 {1,2}A  ，且 (0) 2f  ，求 M 和 m 的值； （2）若 {1}A  ，且 1a  ，记 ( )g a M m  ，求 ( )g a 的最小值． 答案 27．（1）由 (0) 2 2f c 可知 ，……………………………1 分 又   2A 1 2 1 2 ( 1) 0 .ax b x c    ， ，故 ，是方程 的两实根 1-b1+2= a ,c2= a     …………………3 分 1, 2a b  解得 …………4 分  2 2( ) 2 2 ( 1) 1, 2,2f x x x x x         min1 ( ) (1) 1, 1x f x f m   当 时， 即 ……………………………5 分 max2 ( ) ( 2) 10, 10.x f x f M     当 时， 即 ……………………………6 分 （2） 2 ( 1) 0ax b x c   由题意知，方程 有两相等实根x=2,x=1 ∴        a c a b 2 111 ， 即      ac ab 21 ……………………………8 分 ∴f（x）=ax2+（1-2a）x+a, x∈[-2,2] 其对称轴方程为 x=  a a 2 14 1 a2 1 又 a≥1，故 1-      1,2 1 2 1 a ……………………………9 分 ∴M=f（-2）=9a-2 …………………………10 分 m= aa af 4 11)2 12(  ……………………………11 分 g（a）=M+m=9a- a4 1 -1 ……………………………14 分   min 63( ) 1, 1 ( ) .4g a a g a   又 在区间 上为单调递增的， 当 时， = 4 31 ………16 分 2010 年联考题 题组二（5 月份更新） 一、选择题 1. （池州市七校元旦调研）如果函数  cos 2y x ＝3 ＋ 的图像关于点 4 3      ，0 中心对称， 那么| | 的最小值为（ ） （A） 6  （B） 4  （C） 3  (D) 2  答案 A 解析：函数  cos 2y x ＝3 ＋ 的图像关于点 4 3      ，0 中心对称 42 3 2k       13 ( )6k k Z     由此易得 min| | 6   .故选 A 2．（玉溪一中期中文）已知 sin = 5 3 ，cos = 5 4 ，则角 所在的象限是 （ ） A．第一象限. B． 第二象限. C． 第三象限. D． 第四象限. 答案：B 3．（池州市七校元旦调研）已知 a 是实数，则函数 ( ) 1 sinf x a ax  的图象不可能是 ( ) 答案 D 解析 对于振幅大于 1 时，三角函数的周期为 2 , 1, 2T a Ta      ，而 D 不符合要求， 它的振幅大于 1，但周期反而大于了 2 ． 4．（祥云一中三次月考理）在△ABC 中，角 A、B、C 所对的边分别为 a、b、c，已知 B= 3  , 3a ,c=2，则△ABC 的面积为 A． 2 3 B．1 C． 2 3 D． 3 答案：A 5. （肥城市第二次联考）若将函数  tan 04y x        的图像向右平移 6  个单位长 度后，与函数 tan 6y x      的图像重合，则 的最小值为 A． 1 6 B. 1 4 C. 1 3 D. 1 2 答案 D 解析： 6tan tan[ ( ] ta)64 4 6ny x y x x                      向右平移 个单位 164 ( )6 6 2k k k Z           ， 又 min 10 2     .故选 D 6.（祥云一中二次月考理）若关于 x 的方程 Rmxmx 在)0(sin  上恰有 3 个根，且最小 根为 ， 则有 （ ） A. tanm B. cosm C.  tan D.  tan 答案：C 7．（祥云一中三次月考理）使函数 xy sin 递减且函数 xy cos 递增的区间是 A．(  2,2 3 ) B．( 2 32,2   kk )( Zk  ) C．(   kk 2,22 )( Zk  ) D．(  kk 2,22  )( Zk  ) 答案：B 8．（祥云一中三次月考理）函数 1)4(cos)4(sin)( 22   xxxf 是 A．周期为 的奇函数 B．周期为 的偶函数 C．周期为 2 的奇函数 D．周期为 2 的偶函数 答案：A 9.（三明市三校联考）设函数 ( ) sin( ) 1( 0) ( )6f x x f x      的导数 的最大值为 3,则 f(x) 的图象的一条对称轴的方程是 （ ） A． 9 x B． 6 x C． 3 x D． 2 x 答案 A 10．（祥云一中三次月考文）已知 tan 2  ，则 2 2sin sin cos 2cos      A. 5 4 B. 4 5 C. 4 3 D. 3 4 答案：A 11. （哈师大附中、东北师大附中、辽宁省实验中学）函数       )3 80(),sin(2 )02(,1  xx xkx y 的图象如下图，则（ ） A． 6,2 1,2 1  k B． 3,2 1,2 1  k C． 6,2,2 1  k D． 3,2,2  k 答案 A 12．（祥云一中三次月考文）已知函数 ))(2sin()( Rxxxf   ，下面结论错误．．的是 A. 函数 )(xf 的最小正周期为 2 B. 函数 )(xf 是奇函数 C.函数 )(xf 的图象关于直线 x ＝0 对称 D. 函数 )(xf 在区间［0， 2  ］上是增函数 答案：B 二、填空题 1．（肥城市第二次联考）已知 12cos( )4 13    ， 4   是第一象限角，则 sin( 2 )2 sin( )4       的 值是： 。 解析：由于 4   是第一象限角， ∴ 5s ( )4 13in    ，于是 sin( 2 )2 sin( )4       = sin 2( )4 2sin( )4cos( )4          10 13  。 2. （岳野两校联考）已知函数 ( ) 3sin( ), ( ) 3cos( ),f x x g x x       若对任意 ,x R 都有 ( ) ( ),3 3f x f x    则 ( )3g  =________． 答案 0 3. （安庆市四校元旦联考）设函数 1cos 2y x 的图象位于 y 轴右侧所有的对称中心从左 依次为  ,,, 21 nAAA ，则 50A 的坐标是 。 答案 )0,99( 4. （ 祥 云 一 中 二 次 月 考 理 ） 如 果 ,5 1cos  且  是 第 四 象 限 的 角 ， 那 么 )2cos(   = .________________ 答案： 5 62 ； 5. （ 祥 云 一 中 二 次 月 考 理 ） 若 2 1)4tan(   ， 且      2,0  ， 则 .__________________cossin   答案： 5 102 6.（昆明一中三次月考理）关于函数 f (x) sin 2x cos2x  有下列命题： ① y f (x) 的周期为π； ② x = 4  是 y f (x) 的一条对称轴； ③（ 8  ,0）是 y f (x) 的一个对称中心；④ 将 y f (x) 的图象向左平移 4  个单位，可得 到 y 2 sin 2x 的图象，其中正确的命题序号是 （把你认为正确命题的序号都写 上）． 答案：①③ 7．（祥云一中三次月考文）已知 5 23sincos  xx ， 则 )4cos( 2sin15 x x = . 答案：7 8．（祥云一中三次月考理）y=f(x)是关于 x=3 对称的奇函数，f（1）=1, 5 23sincos  xx ， 若 t= )4cos( 2sin15 x x ,则 f(t)= . 答案：-1 题组一（1 月份更新） 一、选择题 1.（2009 昆明一中第三次模拟）若sin 0  且 tan 0  ，则 是( ) A．第一象限角 B．第二象限角 C．第三象限角 D．第四象限角 答案 C 2、（2009 玉溪市民族中学第四次月考）化简 )4tan( 2cos    得-----------（ ） A．sin B．cos C．1+cos2 D．1+sin2 答案 D 3.（2009 青岛一模）设函数 ( ) sin(2 )3f x x   ，则下列结论正确的是 A． ( )f x 的图像关于直线 3x  对称 B． ( )f x 的图像关于点 ( ,0)4  对称 C．把 ( )f x 的图像向左平移 12  个单位，得到一个偶函数的图像 D． ( )f x 的最小正周期为 ，且在[0, ]6  上为增函数 答案 C 4、（2009 江门一模）已知 )(cos3sin)( Rxxxxf  ，函数 )(  xfy 的图象关 于直线 0x 对称，则 的值可以是 A. 2  B 3  C. 4  D. 6  答案 D 5.（2009 日照一模）已知函数 ( ) cos sin ( )f x x x x R  ，给出下列四个命题： ①若 1 2( ) ( )f x f x  ，则 1 2x x  ； ② ( )f x 的最小正周期是 2 ； ③ ( )f x 在区间[ , ]4 4   上是增函数； ④ ( )f x 的图象关于直线 3 4x  对称 A．①②④ B．①③ C．②③ D．③④ 答案 D 6.（2009 牟定一中期中）已知 是第三象限角，并且 sin = 4 5  ，则 tan 等于 ( ) A. 4 3 B 3 4 C.－ 4 3 D.－ 3 4 答案 B 7.（2009 南华一中 12 月月考）要得到一个奇函数，只需将函数 xxxf cos3sin)(  的 图象（ ） A．向右平移   个单位 B．向右平移   个单位 C．向左平移   个单位 D．向左平移   个单位 答案 D 8.（2009 玉溪一中期中）要得到函数 sin(2 )3y x   的图象，只要将函数 xy 2cos 的图 象 （ ） A.向左平移 3  个单位 B.向左平移 12 5 个单位 C.向右平移 3  个单位 D.向右平移 12 5 个单位 答案 A 9.（2009 湛江一模）已知函数 xxxf sincos)(  )( Rx  ，给出下列四个命题： ①若 )()( 21 xfxf  ，则 21 xx  ② )(xf 的最小正周期是 2 ③在区间 ]4,4[  上是增函数 ④ )(xf 的图象关于直线 4 3x 对称 其中真命题是 A ．①②④ B ．①③ C ．②③ D ．③④ 答案 D 10.（2009 云南师大附中）若函数   2 2 tan 1 1, 3f x x x       在 上为单调函数，则 的 取值范围是 A.  , ,2 3 4 2k k k k k Z                     B.  ,4 3k k k Z         C.  , ,2 4 3 2k k k k k Z                     D.  ,3 4k k k Z         答案 A 二、填空题 1.（2009 冠龙高级中学 3 月月考）已知 3( ,0),sin ,2 5      ，则 cos( )  ＝ ______________。 答案 4 5  2.（2009 上海青浦区）把  5cos3cos  化为积的形式，其结果为 ． 答案  coscos42  3.（2009 上海十校联考）函数 4 4sin cosy x x  的单调递增区间是______________． 答案  ,2 4 2 k k k       Z 4.（2009 上海重点九校）方程 2cos( ) 24x   在区间 0, 内的解集 答案 2     三、解答题 1、（2009 广州一模）已知△ABC 的内角 A、B、C 所对的边分别为 a，b，c，且 a=2， cosB= 3 5 ． (1)若 b=4，求 sinA 的值； (2) 若△ABC 的面积 S△ABC=4，求 b，c 的值． 解：(1) ∵cosB= 3 5 >0，且 0