- 167.00 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
小题提速练(四)
一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.设集合A={x|y=lg(x2+3x-4)},B={y|y=21-x2},则A∩B=( )
A.(0,2] B.(1,2]
C.[2,4) D.(-4,0)
解析:选B.∵A={x|x2+3x-4>0}={x|x>1或x<-4},B={y|0<y≤2},∴A∩B=(1,2],故选B.
2.已知复数z满足z(1-i)2=1+i(i为虚数单位),则|z|为( )
A. B.
C. D.1
解析:选B.解法一:因为复数z满足z(1-i)2=1+i,所以z===-+i,所以|z|=,故选B.
解法二:因为复数z满足z(1-i)2=1+i,所以|z|===,故选B.
3.下列函数中,既是偶函数,又在区间(0,+∞)上单调递减的函数是( )
A.y=-x3 B.y=ln|x|
C.y=cos x D.y=2-|x|
解析:选D.显然函数y=2-|x|是偶函数,当x>0时,y=2-|x|==,函数y=在区间(0,+∞)上是减函数.故选D.
4.命题“∀x>0,>0”的否定是( )
A.∃x<0,≤0 B.∃x>0,0≤x≤1
C.∀x>0,≤0 D.∀x<0,0≤x≤1
解析:选B.∵>0,∴x<0或x>1,∴>0的否定是0≤x≤1,∴命题的否定是∃x>0,0≤x≤1,故选B.
5.某单位有老年人27人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为42的样本,则分别应抽取老年人、中年人、青年人的人数是( )
A.7,11,18 B.6,12,18
C.6,13,17 D.7,14,21
解析:选D.因为该单位共有27+54+81=162(人),样本容量为42,所以应当按=的比例分别从老年人、中年人、青年人中抽取样本,且分别应抽取的人数是7、14、21,选D.
6.把边长为1的正方形ABCD沿对角线BD折起,使得平面ABD⊥平面CBD,形成的三棱锥CABD的正视图与俯视图如图所示,则侧视图的面积为( )
A. B.
C. D.
解析:选D.由三棱锥CABD的正视图、俯视图得三棱锥CABD的侧视图为直角边长是的等腰直角三角形,如图所示,所以三棱锥CABD的侧视图的面积为,故选D.
7.已知平面上的单位向量e1与e2的起点均为坐标原点O,它们的夹角为.平面区域D由所有满足=λe1+μe2的点P组成,其中那么平面区域D的面积为( )
A. B.
C. D.
解析:选D.建立如图所示的平面直角坐标系,不妨令单位向量e1=(1,0),e2=,设向量=(x,y),因为=λe1+μe2,所以
即因为所以表示的平面区域D如图中阴影部分所示,所以平面区域D的面积为S=×1×=,故选D.
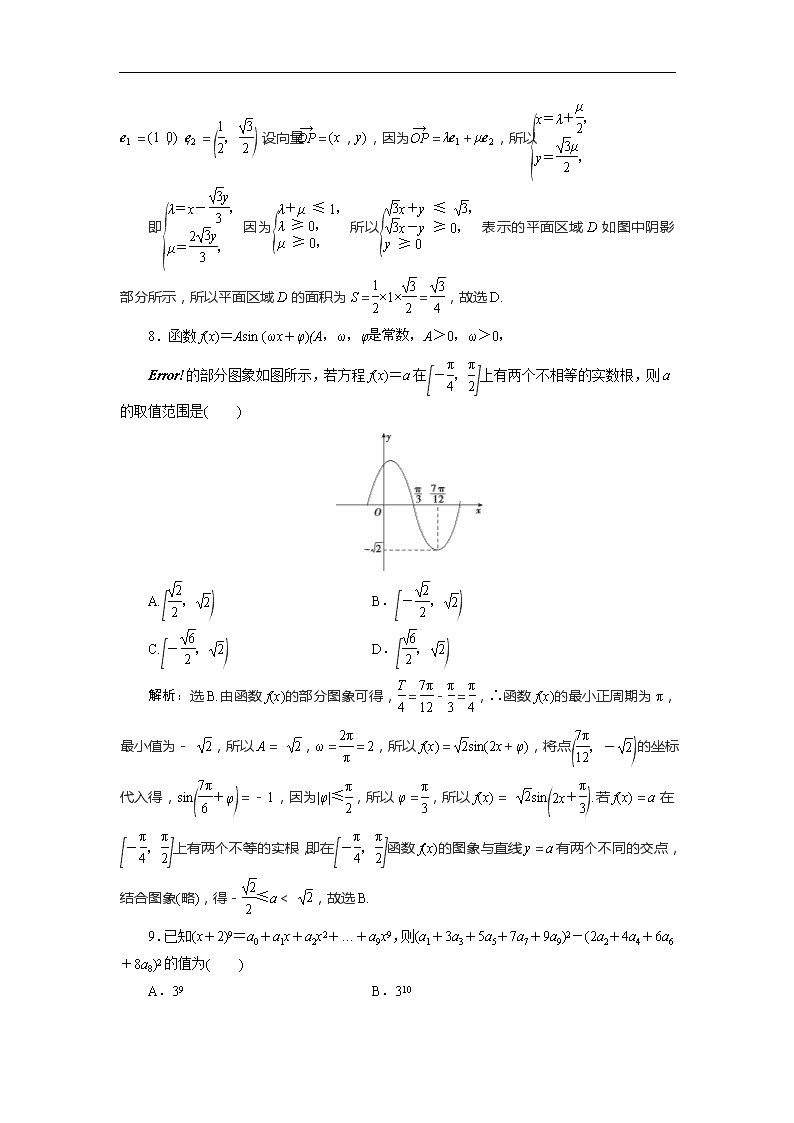
8.函数f(x)=Asin (ωx+φ)
的部分图象如图所示,若方程f(x)=a在上有两个不相等的实数根,则a的取值范围是( )
A. B.
C. D.
解析:选B.由函数f(x)的部分图象可得,=-=,∴函数f(x)的最小正周期为π,最小值为- ,所以A= ,ω==2,所以f(x)=sin(2x+φ),将点的坐标代入得,sin=-1,因为|φ|≤,所以φ=,所以f(x)= sin.若f(x)=a在上有两个不等的实根,即在函数f(x)的图象与直线y=a有两个不同的交点,结合图象(略),得-≤a< ,故选B.
9.已知(x+2)9=a0+a1x+a2x2+…+a9x9,则(a1+3a3+5a5+7a7+9a9)2-(2a2+4a4+6a6+8a8)2的值为( )
A.39 B.310
C.311 D.312
解析:选D.对(x+2)9=a0+a1x+a2x2+…+a9x9两边同时求导,得9(x+2)8=a1+2a2x+3a3x2+…+8a8x7+9a9x8,令x=1,得a1+2a2+3a3+…+8a8+9a9=310,令x=-1,得a1-2a2+3a3-…-8a8+9a9=32.所以(a1+3a3+5a5+7a7+9a9)2-(2a2+4a4+6a6+8a8)2=(a1+2a2+3a3+…+8a8+9a9)(a1-2a2+3a3-…-8a8+9a9)=312,故选D.
10.在平面直角坐标系xOy中,已知双曲线C1:2x2-y2=1,过C1的左顶点引C1的一条渐近线的平行直线,则该直线与另一条渐近线及x轴所围成的三角形的面积为( )
A. B.
C. D.
解析:选C.设双曲线C1的左顶点为A,则A,双曲线的渐近线方程为y=± x,不妨设题中过点A的直线与渐近线y=x平行,则该直线的方程为
y=,即y=x+1.联立,得解得所以该直线与另一条渐近线及x轴所围成的三角形的面积S=|OA|·=××=,故选C.
11.在球O内任取一点P,则点P在球O的内接正四面体中的概率是( )
A. B.
C. D.
解析:选C.设球O的半径为R,球O的内接正四面体的棱长为 a,所以正四面体的高为a,所以R2=+,即a=2R,所以正四面体的棱长为,底面面积为××R=R2,高为,所以正四面体的体积为R3,又球O的体积为R3,所以P点在球O的内接正四面体中的概率为,故选C.
12.设函数f(x)=an=f(n)(n∈N*),若数列{an}是单调递减数列,则实数a的取值范围为( )
A.(-∞,2) B.
C. D.
解析:选B.∵f(x)=∴an=f(n)=∵数列{an}是单调递减数列,
∴解得a<,故选B.
二、填空题(本题共4小题,每小题5分,共20分.)
13.若P(2,-1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程是________________________________________________________________________.
解析:记题中圆的圆心为O,则O(1,0),因为P(2,-1)是弦AB的中点,所以直线AB与直线OP垂直,易知直线OP的斜率为-1,所以直线AB的斜率为1,故直线AB的方程为y+1=x-2,即x-y-3=0.
答案:x-y-3=0
14.某货运员拟运送甲、乙两种货物,每件货物的体积、重量、可获利润以及运输限制如表:
货物
体积(升/件)
重量(千克/件)
利润(元/件)
甲
20
10
8
乙
10
20
10
运输限制
110
100
在最合理的安排下,获得的最大利润为________元.
解析:设该货运员运送甲种货物x件,乙种货物y件,获得的利润为z元,则由题意得
即
z=8x+10y,作出不等式组表示的可行域,如图中阴影部分所示,结合图象可知,当直线z=8x+10y经过点A(4,3)时,目标函数z=8x+10y取得最小值,zmin=62,所以获得的最大利润为62元.
答案:62
15.已知0<x<,则y=+的最小值为________.
解析:解法一:∵y=+=,设5x+6=t,则x=,∵0<x<,∴6<t<
,∴y===,
记f(t)=t+,易知f(t)在(6,9)上是减函数,在上是增函数,∴当t=9时函数f(t)=t+取得最小值,最小值为18,∴当t=9时函数y=取得最小值,最小值为.
解法二:y=+=[2x+(3-2x)]·=
≥=(当且仅当=即x=∈时取等号).
答案:
16.已知函数f(x)=aln x+x2(a>0),若对任意两个不相等的正实数x1,x2,都有>2恒成立,则a的取值范围是________.
解析:因为x1≠x2,所以表示函数f(x)图象上任意两点的连线的斜率,若对任意两个不相等的正实数x1,x2,都有>2恒成立,则f′(x)=x+≥2(a>0)对任意正实数x恒成立,又x+≥2 ,所以2 ≥2,所以a≥1.
答案:a≥1
相关文档
- 2019年高考数学练习题汇总高考模拟2021-06-1611页
- 2019年高考数学练习题汇总10+7满分2021-06-166页
- 2019年高考数学练习题汇总(三)坐标2021-06-162页
- 2019年高考数学练习题汇总1_立体几2021-06-167页
- 2019年高考数学练习题汇总解答题滚2021-06-164页
- 2019年高考数学练习题汇总填空题满2021-06-166页
- 2019年高考数学练习题汇总高考解答2021-06-165页
- 2019年高考数学练习题汇总高考填空2021-06-164页
- 2019年高考数学练习题汇总解答题通2021-06-152页
- 2019年高考数学练习题汇总10+7满分2021-06-156页