- 444.00 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
专练10 函数的图象
命题范围:简单函数图象及其应用.
[基础强化]
一、选择题
1.函数y=2|x|sin 2x的图象可能是( )
A
B
C
D
2.为了得到函数y=log2的图象,可将函数y=log2x图象上所有点的( )
A.纵坐标缩短为原来的,横坐标不变,再向右平移1个单位
B.纵坐标缩短为原来的,横坐标不变,再向左平移1个单位
C.横坐标伸长为原来的2倍,纵坐标不变,再向左平移1个单位
D.横坐标伸长为原来的2倍,纵坐标不变,再向右平移1个单位
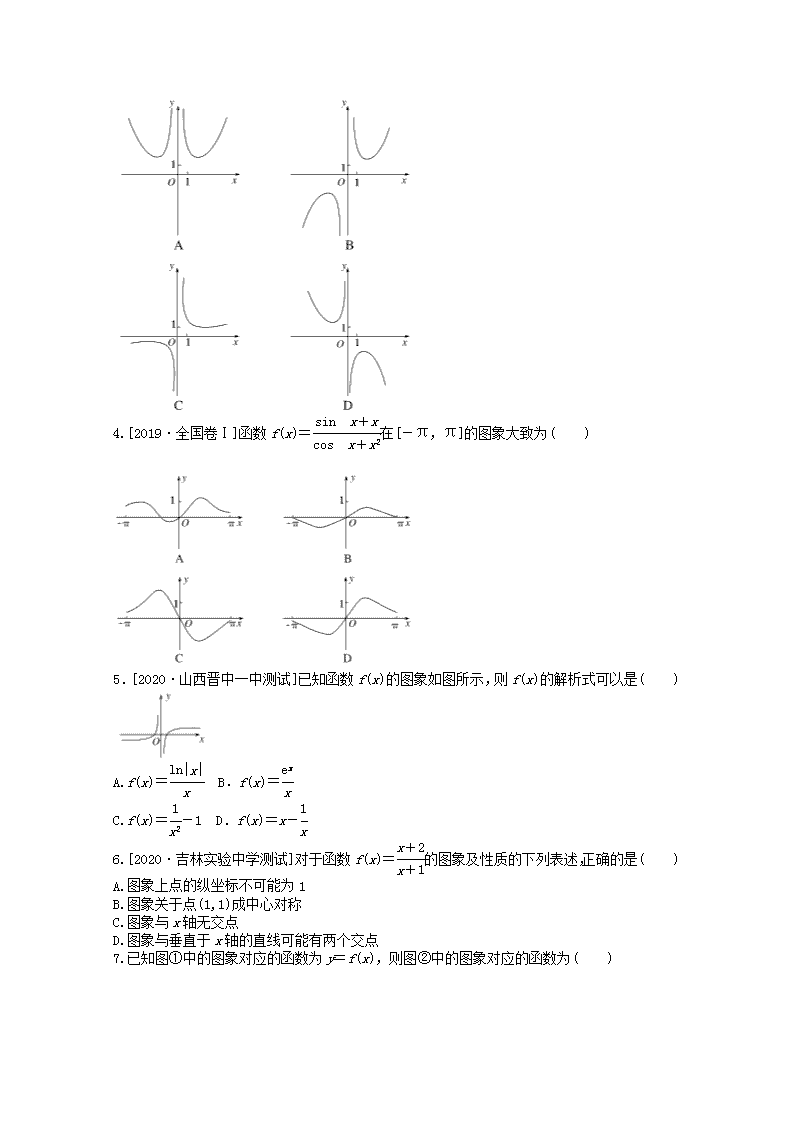
3.函数f(x)=的图象大致为( )
4.[2019·全国卷Ⅰ]函数f(x)=在[-π,π]的图象大致为( )
5.[2020·山西晋中一中测试]已知函数f(x)的图象如图所示,则f(x)的解析式可以是( )
A.f(x)= B.f(x)=
C.f(x)=-1 D.f(x)=x-
6.[2020·吉林实验中学测试]对于函数f(x)=的图象及性质的下列表述,正确的是( )
A.图象上点的纵坐标不可能为1
B.图象关于点(1,1)成中心对称
C.图象与x轴无交点
D.图象与垂直于x轴的直线可能有两个交点
7.已知图①中的图象对应的函数为y=f(x),则图②中的图象对应的函数为( )
A.y=f(|x|) B.y=f(-|x|)
C.y=|f(x)| D.y=-f(|x|)
8.函数f(x)=的图像大致为( )
9.[2020·山西晋中一中测试]函数y=的图象与函数y=2sinπx(-2≤x≤4)的图象的所有交点的横坐标之和等于( )
A.2 B.4
C.6 D.8
二、填空题
10.[2020·安徽师大附中测试]若函数y=f(x)的图象经过点(2,3),则函数y=f(-x)+1的图象必定经过的点的坐标为________.
11.函数f(x)是定义在[-4,4]上的偶函数,其在[0,4]上的图象如图所示,那么不等式<0的解集为________.
12.已知函数y=的图象与函数y=kx-2的图象恰有两个交点,则实数k的取值范围是________.
[能力提升]
13.[2020·湖北武汉示范高中联考]如图,点P在边长为1的正方形边上运动,M是CD的中点,当点P沿A-B-C-M运动时,点P经过的路程x与△APM的面积y的函数y=f(x)的图象的形状大致是( )
14.[2020·雅安中学测试]若关于x的方程 =x+m有两个不同的实根,则实数m的取值范围是( )
A.(2,2) B.[2,2)
C.(-2,2) D.(-2,-2]
15.已知函数y=f(x+1)的图象关于直线x=-1对称,当x∈[-1,+∞)时,f(x+1)是增函数,则不等式f(x-3)-f(x)>0的解集为________.
16.已知函数f(x)=其中m>0.若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是________.
专练10 函数的图象
1.D 由y=2|x|sin 2x知函数的定义域为R,
令f(x)=2|x|sin 2x,则f(-x)=2|-x|sin (-2x)=-2|x|sin 2x.
∵ f(x)=-f(-x),∴ f(x)为奇函数.
∴ f(x)的图象关于原点对称,故排除A,B.
令f(x)=2|x|sin 2x=0,解得x=(k∈Z),
∴ 当k=1时,x=,故排除C.
故选D.
2.A 把函数y=log2x的图象上所有点的纵坐标缩短为原来的,横坐标不变,得到函数y=log2x的图象,再向右平移1个单位,得到函数y=log2(x-1)的图象,即函数y=log2(x-1) =log2的图象.
3.B ∵ y=ex-e-x是奇函数,y=x2是偶函数,
∴ f(x)=是奇函数,图象关于原点对称,排除A选项.
当x=1时,f(1)==e->0,排除D选项.
又e>2,∴ <,∴ e->1,排除C选项.
故选B.
4.D 本题主要考查函数的图象与性质,考查考生的化归与转化能力、数形结合能力、运算求解能力,考查的核心素养是逻辑推理、直观想象、数学运算.
∵f(-x)==-=-f(x),
∴f(x)为奇函数,排除A;
∵f(π)==>0,∴排除C;∵f(1)=,且sin 1>cos 1,∴f(1)>1,∴排除B.故选D.
5.A 由函数的图象可知f(x)为奇函数,故B、C不正确;又当x→+∞时,x-→+∞与图象相矛盾,故D不正确,故选A.
6.A 函数f(x)==1+,∵≠0,∴f(x)≠1.故A正确;显然f(x)的图象关于(-1,1)成中心对称,故B不正确;∵当x=-2时,f(x)=0,故图象与x轴有交点,C不正确;由函数的概念知D不正确.
7.B 图②是由图①y轴左侧图象保留,左右关于y轴对称得,故图②对应的解析式为y=f(-|x|).
8.A 由题意可得函数f(x)的定义域为R,由f(-x)==-=-f(x),知f(x)是奇函数,排除C,D;当x=时,f=>0,排除B.故选A.
9.D 由题意知y==的图象是双曲线,且关于点(1,0)成中心对称,又y=2sinπx的周期为T==2,且也关于点(1,0)成中心对称,
因此两图象的交点也一定关于点(1,0)成中心对称,
再结合图象(如图所示)可知两图象在[-2,4]上有8个交点,
因此8个交点的横坐标之和x1+x2+…+x8=4×2=8.故选D.
10.(-2,4)
解析:由题意得f(2)=3,又y=f(x)与y=f(-x)的图象关于y轴对称,∴y=f(-x)过点(-2,3),∴y=f(-x)+1的图象过点(-2,4).
11.∪
解析:当x∈时,y=cosx>0.
当x∈时,y=cosx<0.
结合y=f(x),x∈[0,4]上的图象知,
当10得f(x-3)>f(x),∴|x-3|>|x|,得x<.
16.(3,+∞)
解析:f(x)的大致图象如图所示,若存在b∈R,使得方程f(x)=b有三个不同的根,只需4m-m20,所以m>3.
相关文档
- 四川省射洪县2018-2019学年高一下2021-06-1612页
- 【数学】广东省珠海市2019-2020学2021-06-1612页
- 【数学】2020届数学(理)一轮复习人教2021-06-169页
- 黑龙江省大庆实验中学2019-2020学2021-06-164页
- 【数学】2020届一轮复习人教版(理)第2021-06-1610页
- 北京市首都师范大学附属中学2019-22021-06-1615页
- 2020秋新教材高中数学第三章函数的2021-06-1620页
- 高考数学模拟试卷 2 (9)2021-06-1611页
- 江苏省南通市如皋市2019-2020学年2021-06-1618页
- 【数学】甘肃省白银市会宁县第四中2021-06-1612页