青海省西宁市2019-2020学年高二下学期期末联考数学（文科）试题 Word版含解析 15页

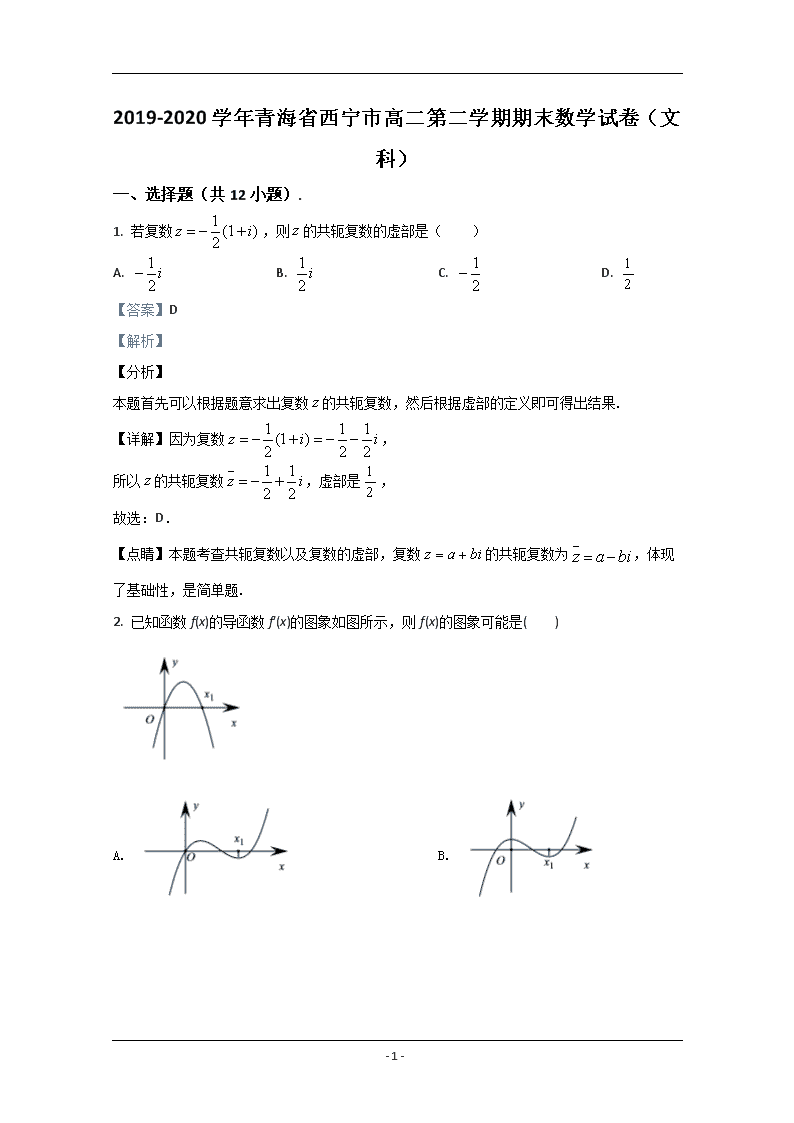
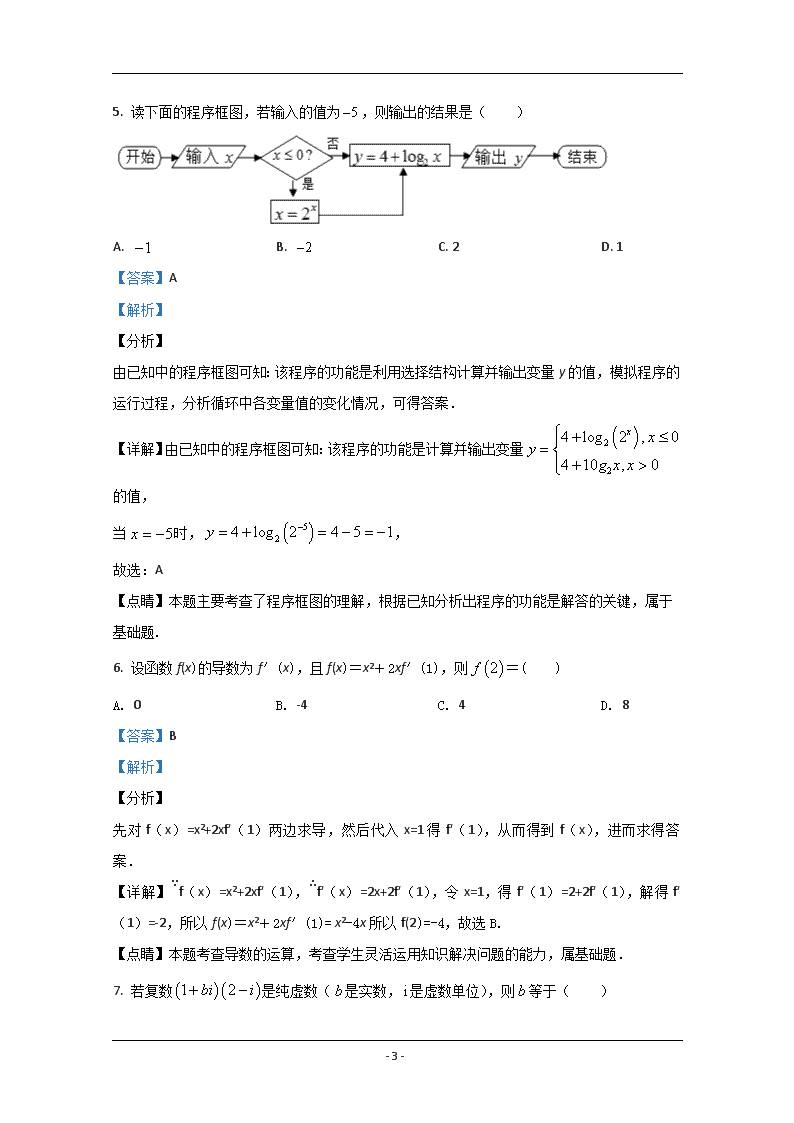
‎2019-2020学年青海省西宁市高二第二学期期末数学试卷（文科）‎ 一、选择题（共12小题）.‎ ‎1. 若复数，则的共轭复数的虚部是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 本题首先可以根据题意求出复数的共轭复数，然后根据虚部的定义即可得出结果.‎ ‎【详解】因为复数，‎ 所以的共轭复数，虚部是，‎ 故选：D．‎ ‎【点睛】本题考查共轭复数以及复数的虚部，复数的共轭复数为，体现了基础性，是简单题.‎ ‎2. 已知函数f(x)的导函数f′(x)的图象如图所示，则f(x)的图象可能是(　　)‎ A. B. ‎ - 15 -‎ C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【详解】由导函数图象可知是的极小值点，‎ 是的极大值点.‎ 故选：D．‎ ‎3. 下列函数中，在(0，＋∞)内为增函数的是(　　)‎ A. y＝sin x B. y＝xe2‎ C. y＝x3－x D. y＝ln x－x ‎【答案】B ‎【解析】‎ ‎【详解】易知A错误；‎ B中y′＝e2＞0在(0，＋∞)内恒成立．‎ C中 不恒成立；D 当 ，故错误选B ‎4. 函数在上的最大值为 A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 利用导数研究函数f（x）在（0，e]上的单调性，由单调性即可求得最大值．‎ ‎【详解】，令，得，令，得，所以函数在上单调递增，在上单调递减，所以当时，函数取极大值，这个极大值也函数在上的最大值，所以，故选A．‎ ‎【点睛】本题考查利用导数研究函数在区间上的最值问题，属基础题．‎ - 15 -‎ ‎5. 读下面的程序框图，若输入的值为，则输出的结果是（ ）‎ A. B. C. 2 D. 1‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 由已知中的程序框图可知：该程序的功能是利用选择结构计算并输出变量y的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．‎ ‎【详解】由已知中的程序框图可知：该程序的功能是计算并输出变量的值，‎ 当时，，‎ 故选：A ‎【点睛】本题主要考查了程序框图的理解，根据已知分析出程序的功能是解答的关键，属于基础题.‎ ‎6. 设函数f(x)的导数为f′(x)，且f(x)＝x2＋2xf′(1)，则＝(　　)‎ A. 0 B. -4 C. 4 D. 8‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 先对f（x）=x2+2xf′（1）两边求导，然后代入x=1得f′（1），从而得到f（x），进而求得答案．‎ ‎【详解】∵f（x）=x2+2xf′（1），∴f′（x）=2x+2f′（1），令x=1，得f′（1）=2+2f′（1），解得f′（1）=-2，所以f(x)＝x2＋2xf′(1)= x2-4x所以f(2)=-4，故选B.‎ ‎【点睛】本题考查导数的运算，考查学生灵活运用知识解决问题的能力，属基础题．‎ ‎7. 若复数是纯虚数（是实数，是虚数单位），则等于（ ）‎ - 15 -‎ A. B. C. D. 2‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 利用复数的运算法则和纯虚数的定义即可得出．‎ ‎【详解】，‎ 由纯虚数的定义可得：且，‎ ‎∴．‎ 故选：A．‎ ‎【点睛】此题为基础题，考查复数的基本概念.‎ ‎8. 已知函数，是的导函数，若，则（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 先求得函数的导数，然后根据列方程，解方程求得的值.‎ ‎【详解】依题意，故，解得.故选C.‎ ‎【点睛】本小题主要考查基本初等函数导数的计算，考查方程的思想，属于基础题.‎ ‎9. 已知为虚数单位，复数满足，是复数的共轭复数，则下列关于复数的说法正确的是（ ）‎ A. B. ‎ C. D. 复数在复平面内表示的点在第四象限 ‎【答案】B ‎【解析】‎ ‎【分析】‎ 由复数的乘法除法运算求出，进而得出答案 - 15 -‎ ‎【详解】由题可得，在复平面内表示的点为，位于第二象限，，故A,C,D错误；，，故B正确；‎ ‎【点睛】本题考查复数的基本运算与几何意义，属于简单题．‎ ‎10. 若，则（ ）‎ A. e B. C. 1 D. 0‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据导数的定义可得，求得导数，即可得到答案．‎ ‎【详解】解：，‎ ‎，则，‎ ‎∴，‎ 故选：D．‎ ‎【点睛】本题考查导数的定义，考查对概念的理解，属于基础题.‎ ‎11. 曲线y=2sinx+cosx在点(π，–1)处的切线方程为 A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 先判定点是否为切点，再利用导数的几何意义求解.‎ ‎【详解】当时，，即点在曲线上．则在点处的切线方程为，即．故选C．‎ ‎【点睛】‎ - 15 -‎ 本题考查利用导数工具研究曲线的切线方程，渗透了直观想象、逻辑推理和数学运算素养．采取导数法，利用函数与方程思想解题．学生易在非切点处直接求导数而出错，首先证明已知点是否为切点，若是切点，可以直接利用导数求解；若不是切点，设出切点，再求导，然后列出切线方程．‎ ‎12. 已知函数的图像在点处的切线与轴平行,则点的坐标是 ( )‎ A. B. ‎ C D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 先设,再对函数求导得由已知得，即可求出切点坐标.‎ ‎【详解】设,由题得 所以,‎ ‎∴.‎ 故选：B.‎ ‎【点睛】本题主要考查对函数求导和导数的几何意义，意在考查学生对该知识的掌握水平和分析推理能力.函数在点处的导数是曲线在处的切线的斜率，相应的切线方程是.‎ 二、填空题（共4小题，每小题5分，满分20分）‎ ‎13. 已知，i是虚数单位，若（1i）（1bi）=a，则的值为_______.‎ ‎【答案】2‎ ‎【解析】‎ 试题分析：由，可得，所以，，故答案为2．‎ ‎【考点】复数相等 - 15 -‎ ‎【名师点睛】本题重点考查复数的基本运算和复数的概念，属于基本题.首先对于复数的四则运算，要切实掌握其运算技巧和常规思路，如 ‎. 其次要熟悉复数的相关基本概念，如复数的实部为、虚部为、模为、共轭复数为.‎ ‎14. 曲线在点处切线的倾斜角为__________.‎ ‎【答案】45°‎ ‎【解析】‎ ‎【分析】‎ 欲求在点（1，3）处的切线倾斜角，先根据导数的几何意义可知k＝y′|x＝1，再结合正切函数的值求出角α的值即可．‎ ‎【详解】y′＝3x2﹣2，切线的斜率k＝3×12﹣2＝1．故倾斜角为45°．‎ 故答案为45°．‎ ‎【点睛】本题考查了导数的几何意义，以及利用斜率求倾斜角，本题属于基础题．‎ ‎15. 曲线在点处的切线方程为__________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 求导，可得斜率，进而得出切线的点斜式方程.‎ ‎【详解】由，得，‎ 则曲线在点处的切线的斜率为，‎ 则所求切线方程为，即.‎ ‎【点睛】求曲线在某点处的切线方程的步骤：①求出函数在该点处的导数值即为切线斜率；②写出切线的点斜式方程；③化简整理.‎ ‎16. 曲线在处的切线的斜率为___________．‎ ‎【答案】‎ ‎【解析】‎ - 15 -‎ ‎【分析】‎ 本题首先可以写出函数的导函数，然后根据导函数的几何意义即可得出结果.‎ ‎【详解】令，则，，‎ 故曲线在处的切线的斜率为，‎ 故答案为：.‎ ‎【点睛】本题考查函数在某点处的切线的斜率，考查导数的几何意义，函数在某点处的导函数值即函数在这点处的切线斜率，考查计算能力，是简单题.‎ 三、解答题（共6小题，满分70分）‎ ‎17. [选修4-4：坐标系与参数方程]:在直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.‎ ‎（1）求曲线，的直角坐标方程；‎ ‎（2）判断曲线，是否相交，若相交，请求出交点间的距离；若不相交，请说明理由.‎ ‎【答案】（1）； （2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由题意，消去参数，即可得到曲线的直角坐标方程，再利用极坐标与直角坐标的互化，即可得到曲线的直角坐标方程；‎ ‎（2）由（1），将代入曲线，求得，，在由曲线，两交点间的距离公式，即可求解．‎ ‎【详解】（1）将，消去参数，得曲线的直角坐标方程为，‎ - 15 -‎ 将展开整理，得，‎ 因为，，‎ 所以曲线的直角坐标方程为.‎ ‎（2）由（1）知曲线是过定点的直线，因为点在曲线的内部，所以曲线与曲线相交.将代入并整理，得，‎ 设曲线，的两交点为，，则，，‎ 故曲线，两交点间的距离 .‎ ‎【点睛】本题主要考查了参数方程与普通方程，极坐标与直角坐标的互化，以及弦长公式的应用，其中解答中熟记互化公式，合理消去参数是解答本题的关键，着重考查了推理与运算能力，属于基础题．‎ ‎18. 已知函数，，若在区间上有最大值5，最小值2．‎ 求a，b的值；‎ 若，在上为单调函数，求实数m的取值范围．‎ ‎【答案】（1）见解析；（2）(－∞，2]∪[6，＋∞)‎ ‎【解析】‎ 解：(1)f(x)＝a(x－1)2＋2＋b－a.‎ 当a>0时，f(x)在[2,3]上为增函数，‎ 故，⇒‎ ‎⇒‎ 当a<0时，f(x)在[2,3]上为减函数，‎ 故⇒‎ - 15 -‎ ‎⇒‎ ‎(2)∵b<1，∴a＝1，b＝0，‎ 即f(x)＝x2－2x＋2.‎ g(x)＝x2－2x＋2－mx ‎＝x2－(2＋m)x＋2，‎ ‎∵g(x)在[2,4]上单调，‎ ‎∴≤2或≥4.‎ ‎∴m≤2或m≥6.‎ 故m的取值范围为(－∞，2]∪[6，＋∞)．‎ ‎19. 已知函数处取得极值．‎ ‎（1）判断和是函数的极大值还是极小值，并说明理由；‎ ‎（2）求函数在点处的切线方程．‎ ‎【答案】（1）为函数的极大值，为函数的极小值；理由见解析；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）求出原函数的导函数，由已知可得，联立求得a，b的值，进一步求出原函数的单调区间，可得为函数的极大值为函数的极小值；‎ ‎（2）直接求出，再由直线方程的点斜式得答案．‎ ‎【详解】（1）由，得，‎ ‎∴，解得．‎ ‎∴．‎ 则．‎ - 15 -‎ ‎∴当时，，‎ 当时，，‎ 则的单调增区间为；‎ 单调减区间．‎ ‎∴为函数的极大值，为函数的极小值；‎ ‎（2）由（1）得，，‎ 则，‎ ‎∴函数在点处的切线方程为，‎ 即．‎ ‎【点睛】本题主要考查了利用导数求函数的单调性，极值，导数的几何意义及切线方程，考查了运算能力，属于中档题.‎ ‎20. 某大学的一个社会实践调查小组，在对大学生就餐“光盘习惯”的调查中，随机发放了120份调查问卷．对收回的100份有效问卷进行统计，得到如下列联表：‎ 做不到光盘 能做到光盘 合计 男 ‎45‎ ‎10‎ ‎55‎ 女 x y ‎45‎ 合计 ‎75‎ m ‎100‎ ‎（1）求表中x，y的值；‎ ‎（2）若在犯错误的概率不超过P的前提下认为良好“光盘习惯”与性别有关，那么根据临界值表，最精确的P的值应为多少？请说明理由．‎ 附：独立性检验统计量，其中．‎ - 15 -‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.840‎ ‎5.024‎ ‎【答案】（1）；（2）；理由见解析.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由表格列方程组，即可求得x，y及m的值；‎ ‎（2）据所给的数据列出列联表，做出观测值，把观测值同临界值进行比较，即可求得最精确的P的值．‎ ‎【详解】解：（1）由题意可知：，解得：，‎ ‎∴，‎ ‎（2），‎ ‎，‎ 所以能在犯错误的概率不超过0.10的前提下认为良好“光盘习惯”与性别有关，即．‎ ‎【点睛】本题考查列联表、独立性检验中的卡方系数计算，考查运算求解能力，属于基础题.‎ ‎21. 在平面直角坐标系中，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l上两点M，N的极坐标分别为（2，0），（），圆C的参数方程（θ为参数）．‎ ‎（Ⅰ）设P为线段MN的中点，求直线OP的平面直角坐标方程；‎ ‎（Ⅱ）判断直线l与圆C的位置关系．‎ - 15 -‎ ‎【答案】见解析 ‎【解析】‎ ‎【分析】‎ ‎（Ⅰ）设P为线段MN的中点，求直线OP的平面直角坐标方程；（Ⅱ）求出圆的圆心与半径，判断圆心与直线的距离与半径的关系，即可判断直线l与圆C的位置关系．‎ ‎【详解】解：（Ⅰ）M，N的极坐标分别为（2，0），（），‎ 所以M、N的直角坐标分别为：M（2，0），N（0，），P为线段MN的中点（1，），‎ 直线OP的平面直角坐标方程y；‎ ‎（Ⅱ）圆C的参数方程（θ为参数）．它的直角坐标方程为：（x﹣2）2+（y）2＝4，‎ 圆的圆心坐标为（2，），半径为2，‎ 直线l上两点M，N的极坐标分别为（2，0），（），‎ 方程为y（x﹣2）（x﹣2），即x+3y﹣20．‎ 圆心到直线的距离为：2，‎ 所以，直线l与圆C相交．‎ ‎【点睛】本题考查圆的参数方程，极坐标方程与直角坐标方程的转化，直线与圆的位置关系，考查计算能力．‎ - 15 -‎ ‎22. 设函数．‎ ‎（1）当时，求函数的极值；‎ ‎（2）当时，讨论函数的单调性．‎ ‎【答案】（1）极小值1，无极大值；（2）当时，单调递减；当时，在和上单调递减，在上单调递增.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）可得函数定义域，解，得．然后分析在1左右两侧导数符号，由极值定义求解；‎ ‎（2）化简可得，按照两根与1的大小关系分类讨论，在定义域内解不等式即可；‎ ‎【详解】（1）函数的定义域为，‎ 当时，．‎ 令，得．‎ 当时，；当时，，‎ ‎∴在上单调递减，在上单调递增，‎ ‎∴的极小值是，无极大值．‎ ‎（2），‎ 当，即时，，在上是减函数；‎ 当，即时，令，得或，令，得，‎ - 15 -‎ 当，时与已知矛盾，舍，‎ 综上，当时，在单调递减；当时，在和上单调递减，在上单调递增；‎ ‎【点睛】本题主要考查导数与函数的极值，导数与函数的单调性，还考查了分类讨论的思想和运算求解的能力，属于中档题.‎ - 15 -‎