数学北师大版（2019）必修第二册：阶段提升课 第三课　平面向量及其应用 学案与作业 8页

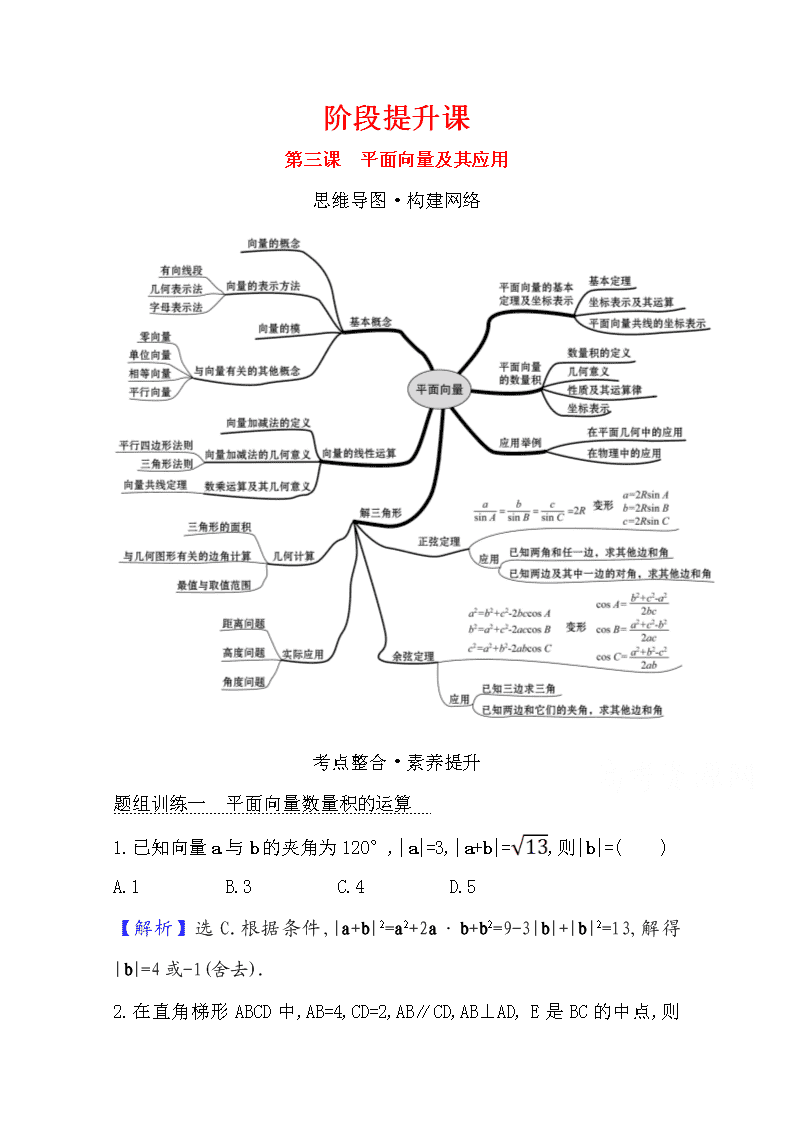
阶段提升课 第三课 平面向量及其应用 思维导图·构建网络 考点整合·素养提升 题组训练一 平面向量数量积的运算 1.已知向量 a 与 b 的夹角为 120°,|a|=3,|a+b|= ,则|b|=( ) A.1 B.3 C.4 D.5 【解析】选 C.根据条件,|a+b| 2 =a 2 +2a·b+b 2 =9-3|b|+|b| 2 =13,解得|b|=4 或-1(舍去). 2.在直角梯形 ABCD 中,AB=4,CD=2,AB∥CD,AB⊥AD,E 是 BC 的中点,则 ·( + )=( ) A.8 B.12 C.16 D.20 【解析】选 D.因为 ·( + )= · + · ,由数量积的几何意 义可得: · 的值为 与 在 方向投影的乘积,又 在 方向的 投影为 AB=2,所以 · =4×2=8,同理 · =4×3=12,所以 ·( + )=8+12=20. 利用数量积的定义、运算律求解数量积 在数量积运算律中,有两个形似实数的完全平方和(差)公式在解题中 的应用较为广泛,即(a+b) 2 =a 2 +2a·b+b 2 ,(a-b) 2 =a 2 -2a·b+b 2 ,上述两个 公式以及(a+b)·(a-b)=a 2 -b 2 这一类似于实数平方差的公式在解题过 程中可以直接应用. 题组训练二 向量平行、垂直的证明 1.已知向量 a=(m,1),b=(2,-3),若(2a-b)⊥b,则 m=( ) A.- B. C. D.- 【 解 析 】 选 B.(2a-b) ⊥ b, 则 (2a-b)·b=(2m-2,5)·(2,-3)=4m-4-15=4m-19=0,所以 m= . 2.若|a|=|b|=1,a⊥b,(2a+3b)⊥(ka-4b),则实数 k 的值为( ) A.-6 B.6 C.-3 D.3 【解析】选 B.因为 a⊥b,所以 a·b=0,因为 ⊥ ,所 以 · =0, 因此 2ka 2 -12b 2 =0 所以 2k-12=0,k=6. 3.已知向量 a=(3,1),b=(m,m+2),c=(m,3),若 a∥b,则 b·c=( ) A.-12 B.-6 C.6 D.3 【解析】选 C.因为 a∥b,所以 3m+6-m=0,解得 m=-3,b=(-3,-1),又 c=(-3,3),所以 b·c=9-3=6. 1.证明共线问题常用的方法 (1)向量 a,b(a≠0)共线⇔存在唯一实数λ使 b=λa. (2)向量 a=(x1,y1),b=(x2,y2)共线⇔x1y2-x2y1=0. (3)向量 a 与 b 共线⇔|a·b|=|a||b|. (4)向量 a 与 b 共线⇔存在不全为零的实数λ1,λ2,使λ1a+λ2b=0. 2.证明平面向量垂直问题的常用方法 a⊥b⇔a·b=0⇔x1x2+y1y2=0,其中 a=(x1,y1),b=(x2,y2). 题组训练三 向量在几何问题中的应用 1.在△ABC 中,已知向量 与 满足 · =0,且 = , 则△ABC 的形状为________. 【解析】因为向量 , 分别表示与向量 , 同方向的单位向量, 所以以 , 为邻边的平行四边形是菱形,根据平行四边形法则作 = + (如图所示). 则 AD 是∠BAC 的平分线.因为( + )· =0,所以∠BAC 的平分线 AD 垂直于 BC,所以 AB=AC,又 cos∠BAC= = ,且∠BAC∈(0,π), 所以∠BAC= ,所以△ABC 为等边三角形. 答案:等边三角形 2. 设 O 是 平 面 ABC 内 一 定 点 ,P 为 平 面 ABC 内 一 动 点 , 若 ( - )·( + )= ( - )·( + )=( - )·( + )=0,则 O 为△ABC 的( ) A.内心 B.外心 C.重心 D.垂心 【 解 析 】 选 B. 若 ( - )·( + )=( - )·( + )=( - )·( + )=0, 可得 ·( + )= ·( + )= ·( + )=0, 即为( - )·( + )=( - )·( + )=( - )·( + )=0, 即有 | 2 =| | 2 , 则 ,故 O为△ABC 的外心. 利用向量解决几何问题的常用思路 把已知问题转化为向量的形式,再通过相应的向量运算去完成,同时, 引入平面向量的坐标可以使向量运算代数化,让平面向量的坐标成为 形与数的载体. 题组训练四 正余弦定理解三角形 1.a,b,c 分别为△ABC 内角 A,B,C 的对边.已知 A= ,sin C=4 sin B. (1)若△ABC 的面积为 4 ,求 b; (2)若 c 2 -b 2 =47,求△ABC 的周长. 【解析】(1)由 sin C=4 sin B,得 c=4 b. 因为△ABC 的面积为 S= bcsin A= bc= b 2 =4 ,所以 b=2. (2)因为 c 2 -b 2 =47,c=4 b,可得 b=1,c=4 , 由余弦定理得 a 2 =b 2 +c 2 -2bccos A=1+48-2×4 × =37,所以 a= , 故△ABC 的周长为 1+4 + . 2.如图,在△ABC 中,AC=2,∠B= ,D 是边 BC 上一点. (1)若∠BAD= ,BD=2,求∠C; (2)若 BD=3CD,求△ACD 面积的最大值. 【解析】(1)因为∠B= ,∠BAD= ,BD=2, 所以 AD= ,在△ADC 中由正弦定理得,sin C= ·AD= ,又 0B⇔a>b⇔sinA>sinB. 关闭 Word 文档返回原板块