高考高职单招数学模拟试题及答案word版 (9) 8页

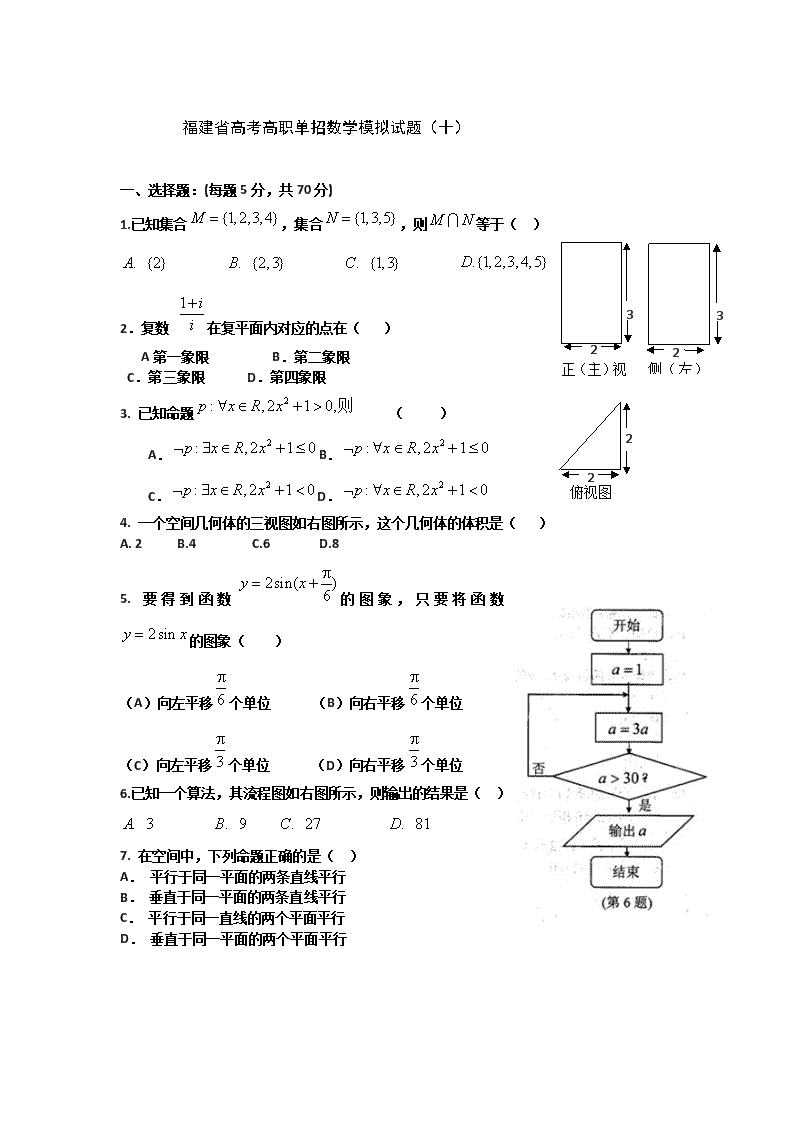
福建省高考高职单招数学模拟试题（十） 一、选择题：(每题 5 分，共 70 分) 1.已知集合 {1,2,3,4}M  ，集合 {1,3,5}N  ，则M N 等于（ ） . {2}A . {2,3}B . {1,3}C .{1,2,3,4,5}D 2．复数 1 i i  在复平面内对应的点在（ ） A 第一象限 B．第二象限 C．第三象限 D．第四象限 3. 已知命题 2: , 2 1 0,p x R x    则 （ ） A． 2: , 2 1 0p x R x     B． 2: , 2 1 0p x R x     C． 2: , 2 1 0p x R x     D． 2: , 2 1 0p x R x     4. 一个空间几何体的三视图如右图所示，这个几何体的体积是（ ） A. 2 B.4 C.6 D.8 5. 要得到函数 2sin( ) 6 y x    的图象，只要将函数 2siny x 的图象（ ） （A）向左平移 6  个单位 （B）向右平移 6  个单位 （C）向左平移 3  个单位 （D）向右平移 3  个单位 6.已知一个算法，其流程图如右图所示，则输出的结果是（ ） . 3A . 9B . 27C . 81D 7. 在空间中，下列命题正确的是（ ） A． 平行于同一平面的两条直线平行 B． 垂直于同一平面的两条直线平行 C． 平行于同一直线的两个平面平行 D． 垂直于同一平面的两个平面平行 正（主）视 侧（左） 俯视图 2 2 2 2 33 8.若 AD为 ABC 的中线，现有质地均匀的粒子散落在 ABC 内，则粒子在 ABD 内的概 率等于（ ） 4. 5 A 3. 4 B 1. 2 C 2. 3 D 9. 计算 sin 240的值为（ ） 3. 2 A  1. 2 B  1. 2 C 3. 2 D ⒑"tan 1"  是 " " 4   的 （ ） A.必要而不充分条件 B.充分而不必要条件 C.充要条件 D.既不充分也不必要条件 11. 下列函数中，在 ),0(  上是减函数的是（ ） .A x y 1  .B 12  xy .C xy 2 .D xy 3log ⒓已知直线的点斜式方程是 2 3( 1)y x    ，那么此直线的倾斜角为（ ） . 6 A  . 3 B  2. 3 C  5. 6 D  13.已知实数 x、 y满足 0 4 x y x y      ≥ ≥0 ≥4 ，则 z x y  的最小值等于（ ） . 0A . 1B . 4C .5D 14、设椭圆的两焦点为 F1、F2，过 F2 作椭圆长轴的垂线交椭圆于点 P，若△F1PF2 为等腰 直角三角形，则椭圆的离心率为（ ） A、 2 2 B、 2 12  C、 22  D、 12  二、 填空题：本大题共 4 个小题，每小题 5 分，共 20 分。 15.如果 0a  ，那么 1 1a a   的最小值是 。 16. 函数 )10(log)(  axxf a 在区间 ]2,[ aa 上的最大值是___________ 17. 在△ ABC中，若 π , 2 4 B b a   ，则 C  ． 18.如图，在矩形 ABCD中， 2 2AB BC ， ，点 E 为 BC的中点，点 F 在边CD上，若 2AB AF    ，则 AE BF   的值是 ． D E F C BA 三、解答题：本大题共 6 小题，共 60 分.解答应写出文字说明、证明过程或演算步骤. 19.（本小题满分 8 分） 已知等差数列  na 满足： 26,7 753  aaa ，  na 的前 n项和为 nS 。 （1）求 na 及 nS ；（2）令 )( 1 1 * 2 Nn a b n n    ，求数列 }{ nb 的前 n项和 nT 。 20.（本小题满分 8 分）设函数 )(2sincos2)( 2 Raaxxxf  ，（1）求函数 f(x)的最 小正周期和单调递增区间；（2）当 [0, ] 6 x   时，f(x)的最大值为 2，求 a的值。 21.（本小题满分 10 分） 如图，四棱锥 P—ABCD 中， PD 平面 ABCD，底面 ABCD为正方形，BC=PD=2，E 为 PC 的中点， . 3 1CBCG  （I）求证： ;BCPC  （II）求三棱锥 C—DEG 的体积； （III）AD 边上是否存在一点 M，使得 //PA 平面 MEG。若存在，求 AM 的长；否则，说 明理由。 22. （本小题满分 10 分）已知椭圆 G： )0(12 2 2 2  ba b y a x 的离心率为 3 6 ，右焦点为  0,22 ，斜率为 1 的直线 l 与椭圆 G 交于 A、B 两点，以 AB 为底边作等腰三角形，顶点为 P（-3,2）。（1）求椭圆 G 的方程；（2）求 PAB 的面积。 23.（本小题满分 12 分） PM2.5 是指大气中直径小于或等于 2.5 微米的颗粒物，也称为可入肺颗粒物. PM2.5 日均值 在 35 微克/立方米以下空气质量为一级；在 35 微克/立方米 ~ 75 微克/立方米之间空气质量 为二级；在 75 微克/立方米以上空气质量为超标． 石景山古城地区 2013 年 2 月 6日至 15 日每天的 PM2.5 监测数据如茎叶图所示． （Ⅰ）计算这 10 天 PM2.5 数据的平均值并判断其是否超标； （Ⅱ）小陈在此期间的某天曾经来此地旅游，求当天 PM2.5 日均监测数据未超标的概率; （Ⅲ）小王在此期间也有两天经过此地，这两天此地 PM2.5 监测数据均未超标.请计算出这 两天空气质量恰好有一天为一级的概率． 24.（本小题满分 12 分）已知函数 xaxxf ln1)(  , a R .（Ⅰ）讨论函数 ( )f x 的单调 区间； （Ⅱ）若函数 )(xf 在 1x 处取得极值，对 x  ( 0 , )  , 2)(  bxxf 恒成立，求实 数b的取值范围. PM2.5 日均值（微克/立方米） 2 1 6 3 7 5 9 6 0 3 8 5 6 10 4 7 福建省春季高考高职单招数学模拟试题（十 ）参考答案 一．选择题（每题 5 分，共 70 分） 题 号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 答 案 C D A C A D B C A A A C B D 15. 3 16. 1 17. 0105 或 12 7 18． 2 19. （本小题满分 8分） 所以， nn bbbT  21 ) 1 11 3 1 3 1 2 1 2 11( 4 1   nn  )1(4   n n 即，数列 nb 的前 n 项和 nT = n 4(n+1) 。 8 分 20. 解：(1)   1) 4 2sin(22sin2cos1  axaxxxf  。。。。。（2分）     2 则f(x)的最小正周期T= …3分  2 2 4 x k       且当2k - k Z 时，f(x)单调递增， 2 2 即  Zkkk      8 , 8 3  为  xf 的单调递增区间。 5分 (2     6 ,0 x 时 12 7 4 2 4   x 2 4 2 8 4 x x      当 ，即 时，sin(2x+ )=1 所以   21,212max  aaxf 8 分 21．（本小题满分 10 分）本题主要考查线面平行与垂直关系、多面体体积计算等 基础知识，考查空间想象能、逻辑思维能力、运算求解能力和探究能力、考 查数形结合思想、化归与转化思想。满分 10 分。 （I）证明： PD 平面 ABCD， BCPD  …………1分 又∵ABCD 是正方形，∴BC⊥CD， …………2分 ∵PD CD=D ∴BC⊥平面 PCD 又∵PC面 PBC ∴PC⊥BC …………4分 （II）解：∵BC⊥平面 PCD，∴GC 是三棱锥 G—DEC 的高。 …………5分 ∵E是 PC 的中点， 1)22 2 1( 2 1 2 1   PDCEDC SS ……6分 9 21 3 2 3 1 3 1   DECDECGDEGC SGCVV …………7分 （III）连结 AC，取 A C 中点 O，连结 EO、GO，延长 GO 交 AD 于点 M， 则 PA//平面 MEG。下面证明之 ∵E为 PC 的中点，O是 AC 的中点，∴EO//PA， 又 MEGPAMEGEO 平面平面  , ∴PA//平面 MEG…………9分 在正方形 ABCD 中，∵O是 AC 中点， OCG ≌ OAM , 3 2  CGAM ∴所求 AM 的长为 . 3 2 10 分 22 ．（ 2 ） 设 直 线 l 的 方 程 为 y=x+m, 由       1 412 22 yx mxy 得 )1(012364 22  mmxx 。。。。。。（5分） 设 A，B的坐标分别为     ),(,,, 212211 xxyxyx  AB 中点为  00 , yxE ，则 4 , 4 3 2 00 21 0 mmxymxxx    。。。。。。（6分） 因为 AB 是等腰三角 形 PAB 的底边，所 以 PE ,AB 所以 PE 的斜率 ,1 4 33 4 2     m m k 解得 m=2（。。。。。。。7分） 此时方程（1）为 ,0124 2  xx 解得 ,0,3 21  xx 所以 2,1 21  yy 所以 23AB 。（。。。。。8分）此时，点 P（-3,2）到直线 AB：x-y+2=0 的距离 d= 2 23 2 223   ,（。。。。。。。。。。9分） 所以 PAB 的面积 . 2 9 2 1  dABS （。。。。。。。。。。10 分） 23．（本小题满分 12 分） 解：（Ⅰ） 21 26 37 59 60 63 85 86 104 107 64.8 10 X            ， …2 分 64.8在 35与 75 之间，空气质量属于二级，未超标. ……3 分 （Ⅱ）记“当天 PM2.5 日均监测数据未超标”为事件 A, 2 4 3( ) 10 5 P A    . 6分 （Ⅲ）由茎叶图知 PM2.5数据在0 ~ 35之间的有 21、26，PM2.5数据在35 ~ 75之 间的有 37、59、60、63，从这六个数据中，任意抽取 2个的结果有： (21，37)，(21，59)，(21 ，60)，(21，63)，(26，37)，(26，59)，(26 ，60)， (26，63)，(21，26)，(37，59)，(37 ，60)，(37，63)，(59，60)，(59，63)， (60 ，63) ． 共有 15 个. …………10分 记“这两天此地 PM2.5 监测数据均未超标且空气质量恰好有一天为一级” 为 事件 B, 8( ) 15 P B  . 12分 24． 解：（Ⅰ）在区间  0, 上, 1 1( ) axf x a x x     . 1 分 ①若 0a  ,则 ( ) 0f x  , ( )f x 是区间  0, 上的减函数； ……………3分 ②若 0a  ,令 ( ) 0f x  得 1x a  . 在区间 1(0, ) a 上, ( ) 0f x  ,函数 ( )f x 是减函数; 在区间 1( , ) a  上, ( ) 0f x  ,函数 ( )f x 是增函数; 综上所述，①当 0a  时, ( )f x 的递减区间是  0, ，无递增区间； ②当 0a  时， ( )f x 的递增区间是 1( , ) a  ，递减区间是 1(0, ) a . 5 分 （II）因为函数 )(xf 在 1x 处取得极值，所以 (1) 0f   解得 1a ，经检验满足题意. 7 分 由已知 ( ) 2,f x bx  则 1 ln( ) 2,1 xf x bx b x x      …8分 令 x x x xg ln11)(  ，则 2 2 2 1 1 ln ln -2( ) x xg x x x x      10 分 易得 )(xg 在  2,0 e 上递减，在  ,2e 上递增， 11 分 所以 2 2 min 11)()( e egxg  ，即 2 11b e   ． 12 分