- 368.52 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
高考模拟试卷
高考模拟试卷(一)
(时间:150分钟 满分:200分)
数学Ⅰ试题
一、填空题(本大题共14小题,每小题5分,共70分)
1.已知集合A={2,5,6},B={3,5},则集合A∪B=________.
答案 {2,3,5,6}
2.设复数z满足(2+i)z=,i为虚数单位,则复数z在复平面内对应的点在第________象限.
答案 四
解析 由(2+i)z=|-i|==2,
得z===-i,
∴复数z在复平面内对应的点的坐标为,
在第四象限.
3.(2018·苏锡常镇四市调研)如图是一个算法流程图,若输入值x∈[0,2],则输出值S的取值范围是________.
答案 [0,1]
解析 由题意得S=
所以当x∈[0,1)时,S=1;
当x∈[1,2]时,S∈[0,1],
综上所述,输出值S的取值范围是[0,1].
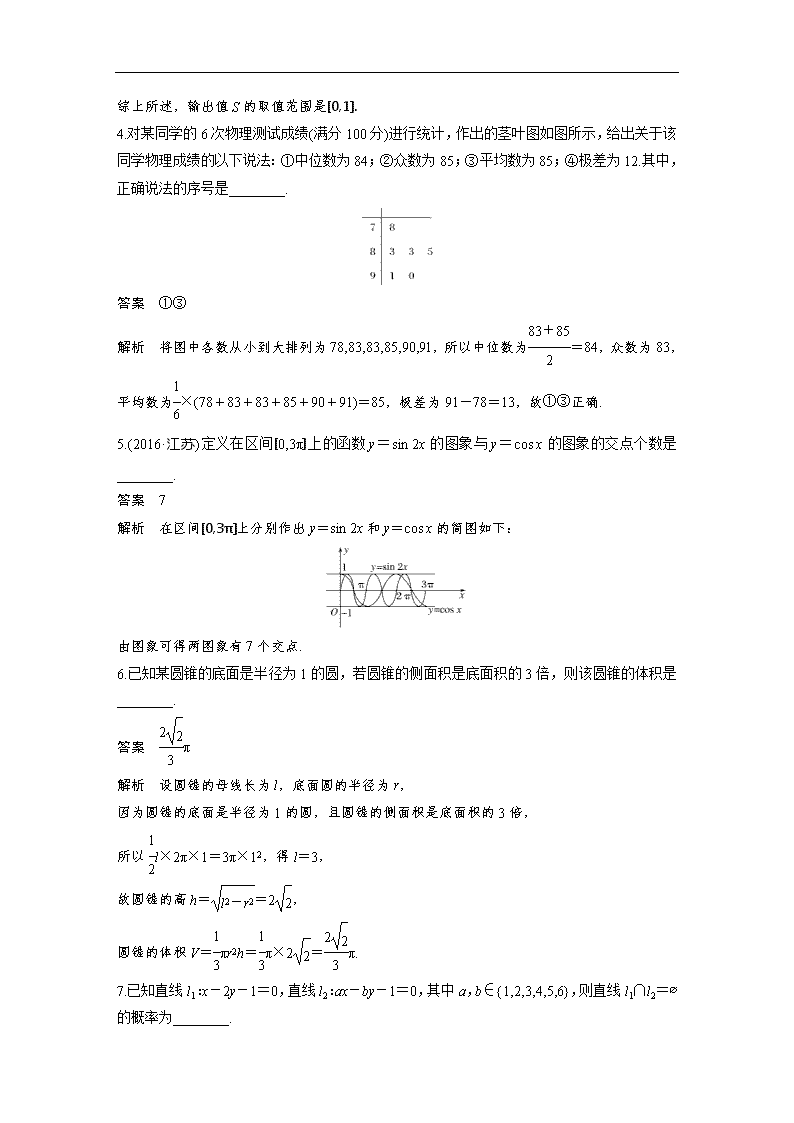
4.对某同学的6次物理测试成绩(满分100分)
进行统计,作出的茎叶图如图所示,给出关于该同学物理成绩的以下说法:①中位数为84;②众数为85;③平均数为85;④极差为12.其中,正确说法的序号是________.
答案 ①③
解析 将图中各数从小到大排列为78,83,83,85,90,91,所以中位数为=84,众数为83,平均数为×(78+83+83+85+90+91)=85,极差为91-78=13,故①③正确.
5.(2016·江苏)定义在区间[0,3π]上的函数y=sin 2x的图象与y=cos x的图象的交点个数是________.
答案 7
解析 在区间[0,3π]上分别作出y=sin 2x和y=cos x的简图如下:
由图象可得两图象有7个交点.
6.已知某圆锥的底面是半径为1的圆,若圆锥的侧面积是底面积的3倍,则该圆锥的体积是________.
答案 π
解析 设圆锥的母线长为l,底面圆的半径为r,
因为圆锥的底面是半径为1的圆,且圆锥的侧面积是底面积的3倍,
所以l×2π×1=3π×12,得l=3,
故圆锥的高h==2,
圆锥的体积V=πr2h=π×2=π.
7.已知直线l1:x-2y-1=0,直线l2:ax-by-1=0,其中a,b∈{1,2,3,4,5,6},则直线l1∩l2=∅的概率为________.
答案
解析 ∵a,b∈{1,2,3,4,5,6},
∴a,b各有6种取法,∴总事件数是36.
而满足条件的只有两组数a=2,b=4;a=3,b=6.
∴P==.
8.已知点F1,F2分别是双曲线-=1(a>0,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围是__________.
答案 (1,1+)
解析 方法一 设A,B,
则=,=.
又·=4c2-2>0,
即e4-6e2+1<0,所以10,b>0,
∵a+3b=7,∴a+1+3(b+2)=14,
则+=1,
那么
=++
≥+2=+2×=,
当且仅当2(a+1)=(b+2)时,取等号.
∴+的最小值为.
14.已知函数y=f(x)是定义域为R的偶函数.当x≥0时,f(x)=若关于x的方程f2(x)+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是____________.
答案 ∪
解析 依题意f(x)在(-∞,-2)和(0,2)上递增,
在(-2,0)和(2,+∞)上递减,
当x=±2时,函数取得极大值;
当x=0时,取得极小值0.
要使关于x的方程f2(x)+af(x)+b=0,a,b∈R有且仅有6个不同实数根,
设t=f(x),则t2+at+b=0必有两个根t1,t2,
则有两种情况符合题意:
①t1=,且t2∈,
此时-a=t1+t2,
则a∈;
②t1∈(0,1],t2∈,
此时同理可得a∈.
综上可得a的取值范围是∪.
二、解答题(本大题共6小题,共90分)
15.(14分)如图,已知△ABC是正三角形,EA,CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
(1)FD∥平面ABC;
(2)AF⊥平面EDB.
证明 (1)取AB的中点M,连结FM,MC.
∵F,M分别是BE,BA的中点,
∴FM∥EA,FM=EA=a.
∵EA,CD都垂直于平面ABC,
∴CD∥EA,
∴CD∥FM.
又∵DC=a,∴FM=DC,
∴四边形FMCD是平行四边形,
∴FD∥MC.
∵FD⊄平面ABC,MC⊂平面ABC,
∴FD∥平面ABC.
(2)∵M是AB的中点,△ABC是正三角形,
∴CM⊥AB.
又∵AE⊥平面ABC,CM⊂平面ABC,∴CM⊥AE,
又∵AB∩AE=A,AB,AE⊂平面EAB,
∴CM⊥平面EAB,
又AF⊂平面EAB,
∵CM⊥AF.
又∵CM∥FD,
∴FD⊥AF.
∵F是BE的中点,EA=AB,
∴AF⊥BE.
又∵FD∩BE=F,FD,BE⊂平面EDB,
∴AF⊥平面EDB.
16.(14分)已知向量a=(cos α,sin α),b=(cos x,sin x),c=(sin x+2sin α,cos x+2cos α),其中0<α
相关文档
- 2019年高考数学练习题汇总(七)计数2021-06-163页
- 2019年高考数学练习题汇总高考解答2021-06-167页
- 2019年高考数学练习题汇总小题提速2021-06-166页
- 2019年高考数学练习题汇总高考模拟2021-06-1611页
- 2019年高考数学练习题汇总10+7满分2021-06-166页
- 2019年高考数学练习题汇总(三)坐标2021-06-162页
- 2019年高考数学练习题汇总1_立体几2021-06-167页
- 2019年高考数学练习题汇总解答题滚2021-06-164页
- 2019年高考数学练习题汇总填空题满2021-06-166页
- 2019年高考数学练习题汇总高考解答2021-06-165页