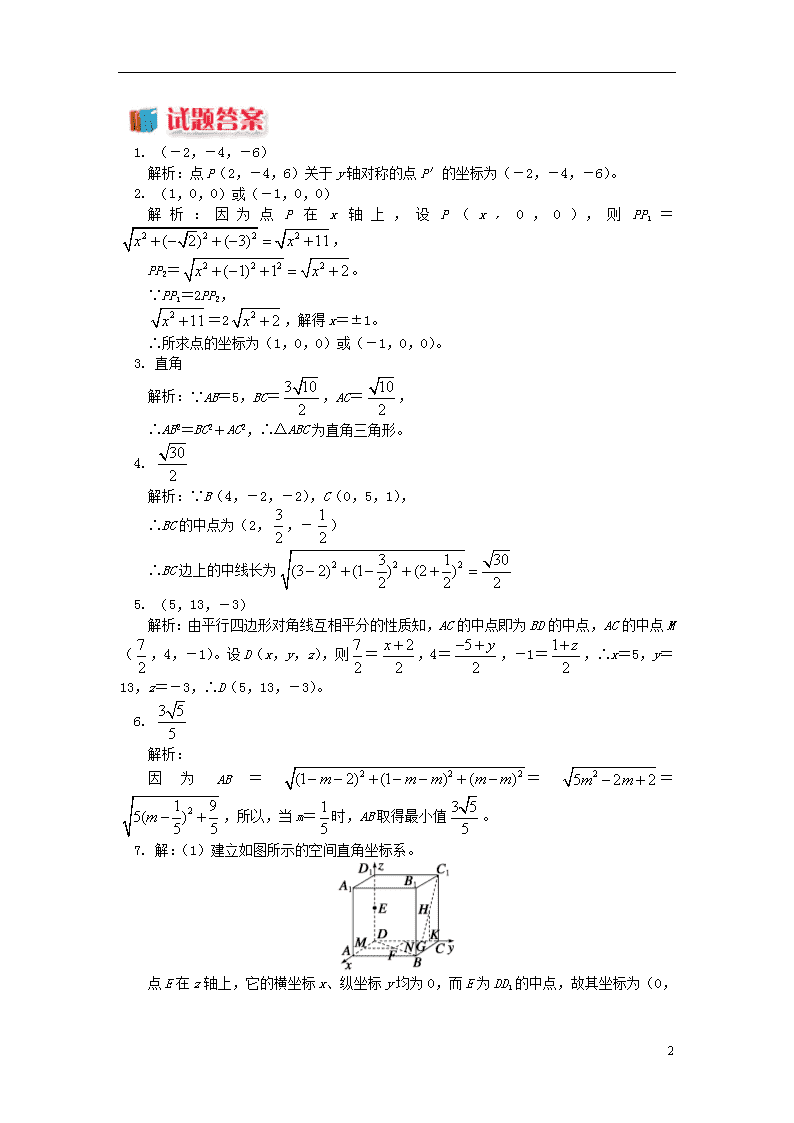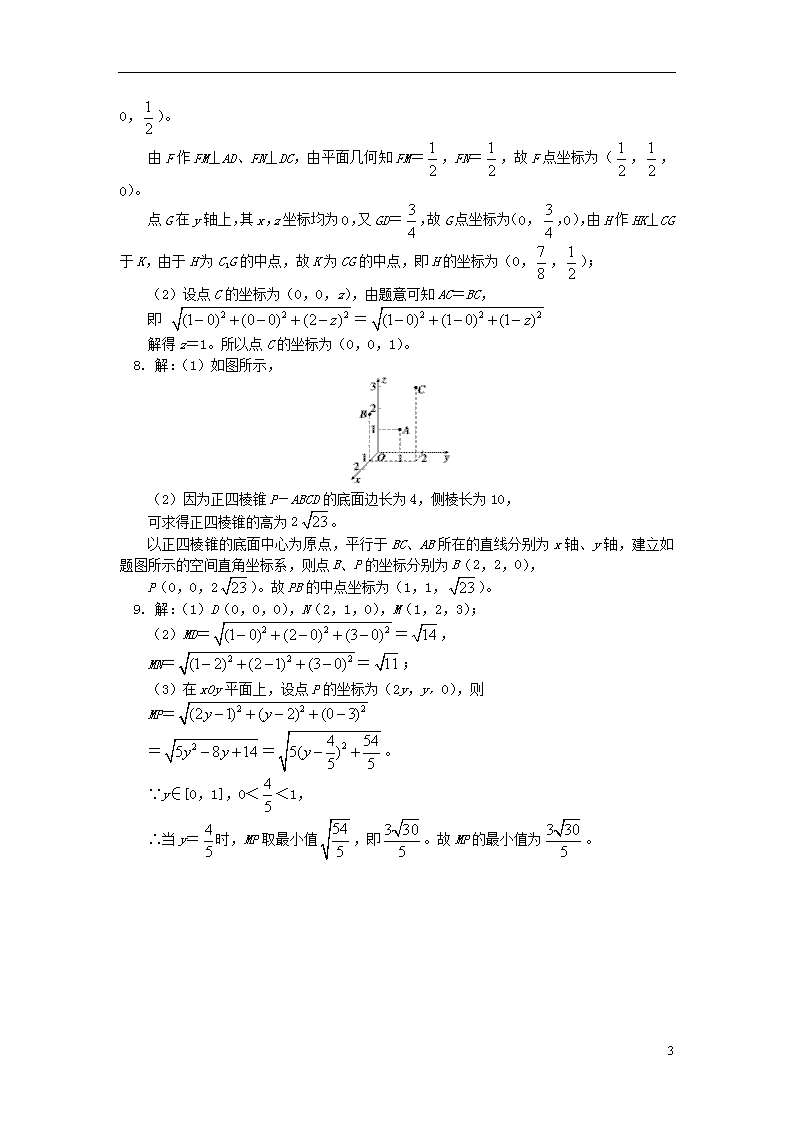2020高中数学 第2章 平面解析几何初步 第三节 空间直角坐标系2 空间两点间距离习题 苏教版 3页

空间两点间距离 ‎（答题时间：40分钟）‎ ‎1. （南京检测）在空间直角坐标系中，点P（2，－4，6）关于y轴对称的点P′的坐标为____________。‎ ‎2. 点P在x轴上，它到点P1（0，，3）的距离是到点P2（0，1，－1）的距离的2倍，则点P的坐标是________。‎ ‎3. 已知△ABC顶点坐标分别为A（－1，2，3）、B（2，－2，3）、C（，，3），则△ABC为________三角形。‎ ‎4. （福建八县联考）已知△ABC三个顶点的坐标分别为A（3，1，2）、B（4，－2，－2）、C（0，5，1），则BC边上的中线长________。‎ ‎5. 已知平行四边形ABCD，且A（4，1，3）、B（2，－5，1）、C（3，7，－5），则顶点D的坐标为__________。‎ ‎**6. 已知点A（2，m，m），B（1－m，1－m，m），则AB的最小值为________。‎ ‎**7.（1）在棱长为1的正方体ABCD—A1B‎1C1D1中，E、F分别是D1D、BD的中点，G在棱CD上，且CG＝CD，H为C‎1G的中点，试建立适当的坐标系，写出E、F、G、H的坐标。‎ ‎（2）（辽宁实验中学检测）在空间直角坐标系中，在z轴上求一点C，使得点C到点A（1，0，2）与点B（1，1，1）的距离相等。‎ ‎*8.（1）在空间直角坐标系中画出下列各点（不写画法，保留作图痕迹）：A（0，1，1），B（1，0，2），C（1，2，3）；‎ ‎（2）已知正四棱锥P－ABCD的底面边长为4，侧棱长为10，试建立适当的空间直角坐标系，写出PB中点的坐标。‎ ‎***9. 长方体ABCD－A1B‎1C1D1中，AB＝BC＝2，D1D＝3，点M是B‎1C1的中点，点N是AB的中点。建立如图所示空间直角坐标系。‎ ‎（1）写出点D、N、M的坐标；‎ ‎（2）求线段MD、MN的长度；‎ ‎（3）设点P是线段DN上的动点，求MP的最小值。‎ 3‎ ‎1. （－2，－4，－6）‎ 解析：点P（2，－4，6）关于y轴对称的点P′的坐标为（－2，－4，－6）。‎ ‎2. （1，0，0）或（－1，0，0）‎ 解析：因为点P在x轴上，设P（x，0，0），则PP1＝，‎ PP2＝。‎ ‎∵PP1＝2PP2，‎ ‎＝2，解得x＝±1。‎ ‎∴所求点的坐标为（1，0，0）或（－1，0，0）。‎ ‎3. 直角 解析：∵AB＝5，BC＝，AC＝，‎ ‎∴AB2＝BC2＋AC2，∴△ABC为直角三角形。‎ ‎4. ‎ 解析：∵B（4，－2，－2），C（0，5，1），‎ ‎∴BC的中点为（2，，－）‎ ‎∴BC边上的中线长为 ‎5. （5，13，－3）‎ 解析：由平行四边形对角线互相平分的性质知，AC的中点即为BD的中点，AC的中点M（，4，－1）。设D（x，y，z），则＝，4＝，－1＝，∴x＝5，y＝13，z＝－3，∴D（5，13，－3）。‎ ‎6. ‎ 解析：‎ 因为AB＝＝＝，所以，当m＝时，AB取得最小值。‎ ‎7. 解：（1）建立如图所示的空间直角坐标系。‎ 点E在z轴上，它的横坐标x、纵坐标y均为0，而E为DD1‎ 3‎ 的中点，故其坐标为（0，0，）。‎ 由F作FM⊥AD、FN⊥DC，由平面几何知FM＝，FN＝，故F点坐标为（，，0）。‎ 点G在y轴上，其x，z坐标均为0，又GD＝，故G点坐标为（0，，0），由H作HK⊥CG于K，由于H为C‎1G的中点，故K为CG的中点，即H的坐标为（0，，）；‎ ‎（2）设点C的坐标为（0，0，z），由题意可知AC＝BC，‎ 即 ＝‎ 解得z＝1。所以点C的坐标为（0，0，1）。‎ ‎8. 解：（1）如图所示，‎ ‎（2）因为正四棱锥P－ABCD的底面边长为4，侧棱长为10，‎ 可求得正四棱锥的高为2。‎ 以正四棱锥的底面中心为原点，平行于BC、AB所在的直线分别为x轴、y轴，建立如题图所示的空间直角坐标系，则点B、P的坐标分别为B（2，2，0），‎ P（0，0，2）。故PB的中点坐标为（1，1，）。‎ ‎9. 解：（1）D（0，0，0），N（2，1，0），M（1，2，3）；‎ ‎（2）MD＝＝，‎ MN＝＝；‎ ‎（3）在xOy平面上，设点P的坐标为（2y，y，0），则 MP＝‎ ‎＝＝。‎ ‎∵y∈[0，1]，0＜＜1，‎ ‎∴当y＝时，MP取最小值，即。故MP的最小值为。‎ 3‎