- 626.66 KB
- 2021-06-19 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2019届高三数学专题练习外接球
1.正棱柱,长方体的外接球球心是其中心
例1:已知各顶点都在同一球面上的正四棱柱的高为,体积为,则这个球的表面积是( )
A. B. C. D.
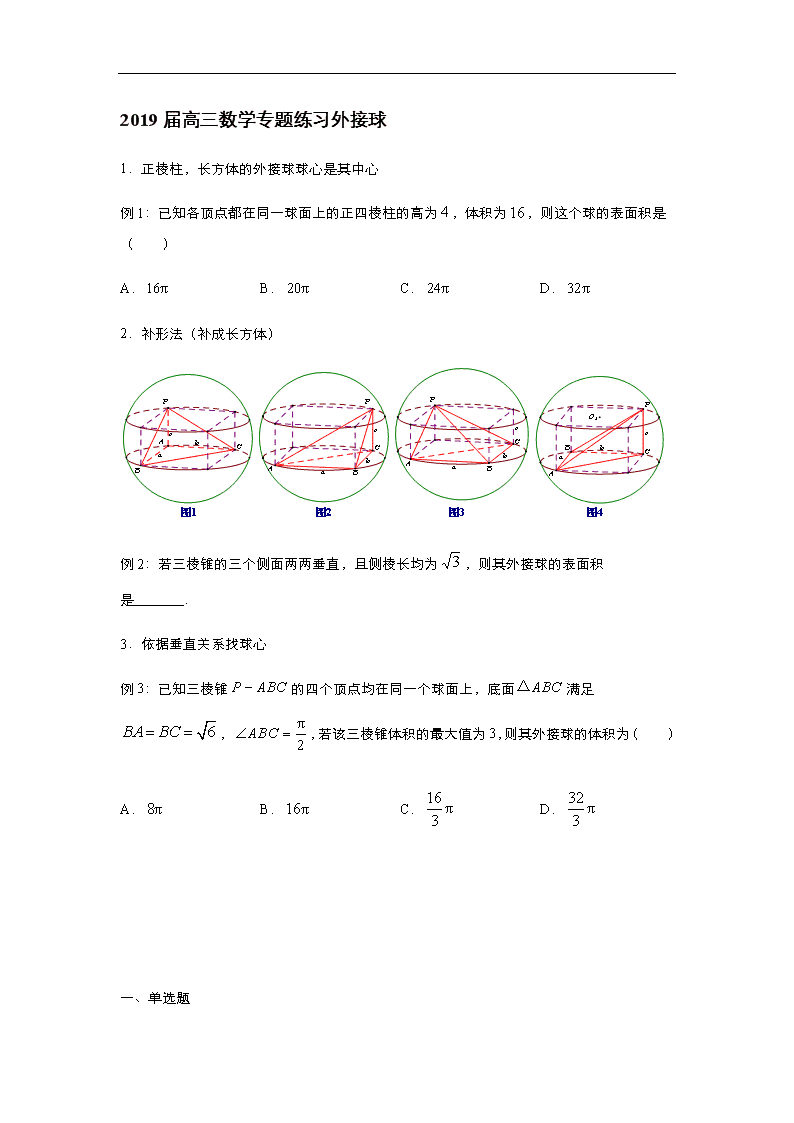
2.补形法(补成长方体)
例2:若三棱锥的三个侧面两两垂直,且侧棱长均为,则其外接球的表面积是 .
3.依据垂直关系找球心
例3:已知三棱锥的四个顶点均在同一个球面上,底面满足,,若该三棱锥体积的最大值为3,则其外接球的体积为( )
A. B. C. D.
一、单选题
1.棱长分别为2、、的长方体的外接球的表面积为( )
A. B. C. D.
2.设三棱柱的侧棱垂直于底面,所有棱的长都为,顶点都在一个球面上,则该球的表面积为( )
A.12π B.28π C.44π D.60π
3.把边长为3的正方形沿对角线对折,使得平面平面,则三棱锥的外接
球的表面积为( )
A. B. C. D.
4.某几何体是由两个同底面的三棱锥组成,其三视图如下图所示,则该几何体外接球的面积为( )
A. B. C. D.
5.三棱锥的所有顶点都在球的表面上,平面,,,则球的表面积为( )
A. B. C. D.
6.如图是边长为1的正方体,是高为1的正四棱锥,若点,,,,在同一个球面上,则该球的表面积为( )
A. B. C. D.
7.已知球的半径为,,,三点在球的球面上,球心到平面的距离为,,,则球的表面积为( )
A. B. C. D.
8.已知正四棱锥(底面四边形是正方形,顶点在底面的射影是底面的中心)的各顶点都在同一球面上,底面正方形的边长为,若该正四棱锥的体积为,则此球的体积为( )
A. B. C. D.
9.如图,在中,,,点为的中点,将沿折起到的位置,使,连接,得到三棱锥.若该三棱锥的所有顶点都在同一球面上,
则该球的表面积是( )
A. B. C. D.
10.四面体中,,,
,则此四面体外接球的表面积为( )
A. B. C. D.
11.将边长为2的正沿着高折起,使,若折起后四点都在球的表面上,则球的表面积为( )
A. B. C. D.
12.在三棱锥中,,,则该三棱锥的外接球的表面积为( )
A. B. C. D.
二、填空题
13.棱长均为6的直三棱柱的外接球的表面积是_________.
14.已知棱长都相等正四棱锥的侧面积为,则该正四棱锥内切球的表面积为________.
15.已知三棱柱的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为,,,,则此球的表面积等于______.
16.在三棱锥中,,,,,则三棱锥外接球的体积的最小值为_____.
1.正棱柱,长方体的外接球球心是其中心
例1:已知各顶点都在同一球面上的正四棱柱的高为,体积为,则这个球的表面积是( )
A. B. C. D.
【答案】C
【解析】,,,,故选C.
2.补形法(补成长方体)
例2:若三棱锥的三个侧面两两垂直,且侧棱长均为,则其外接球的表面积是 .
【答案】
【解析】,.
3.依据垂直关系找球心
例3:已知三棱锥的四个顶点均在同一个球面上,底面满足,,若该三棱锥体积的最大值为3,则其外接球的体积为( )
A. B. C. D.
【答案】D
【解析】因为是等腰直角三角形,所以外接球的半径是,设外接球的半径是,球心到该底面的距离,如图,则,,由题设,
最大体积对应的高为,故,即,解之得,
所以外接球的体积是,故答案为D.
一、单选题
1.棱长分别为2、、的长方体的外接球的表面积为( )
A. B. C. D.
【答案】B
【解析】设长方体的外接球半径为,由题意可知:,则:,该长方体的外接球的表面积为.本题选择B选项.
2.设三棱柱的侧棱垂直于底面,所有棱的长都为,顶点都在一个球面上,则该球的表面积为( )
A.12π B.28π C.44π D.60π
【答案】B
【解析】设底面三角形的外接圆半径为,由正弦定理可得:,则,
设外接球半径为,结合三棱柱的特征可知外接球半径,
外接球的表面积.本题选择B选项.
3.把边长为3的正方形沿对角线对折,使得平面平面,则三棱锥的外接
球的表面积为( )
A. B. C. D.
【答案】C
【解析】把边长为3的正方形沿对角线对折,使得平面平面,
则三棱锥的外接球直径为,外接球的表面积为,故选C.
4.某几何体是由两个同底面的三棱锥组成,其三视图如下图所示,则该几何体外接球的面积为( )
A. B. C. D.
【答案】C
【解析】由题可知,该几何体是由同底面不同棱的两个三棱锥构成,其中底面是棱长为的正三角形,一个是三条侧棱两两垂直,且侧棱长为的正三棱锥,另一个是棱长为的正四面体,如图所示:
该几何体的外接球与棱长为a的正方体的外接球相同,因此外接球的直径即为正方体的体对角线,所以,所以该几何体外接球面积,故选C.
5.三棱锥的所有顶点都在球的表面上,平面,,,则球的表面积为( )
A. B. C. D.
【答案】D
【解析】因为,,所以,,
因此三角形外接圆半径为,
设外接球半径为,则,,故选D.
6.如图是边长为1的正方体,是高为1的正四棱锥,若点,,,,在同一个球面上,则该球的表面积为( )
A. B. C. D.
【答案】D
【解析】如图所示,连结,,交点为,连结,
易知球心在直线上,设球的半径,在中,由勾股定理有:,即:,解得:,则该球的表面积.本题选择D选项.
7.已知球的半径为,,,三点在球的球面上,球心到平面的距离为,,,则球的表面积为( )
A. B. C. D.
【答案】D
【解析】由余弦定理得:,
设三角外接圆半径为,由正弦定理可得:,则,
又,解得:,则球的表面积.本题选择D选项.
8.已知正四棱锥(底面四边形是正方形,顶点P在底面的射影是底面的中心)的各顶点都在同一球面上,底面正方形的边长为,若该正四棱锥的体积为,则此球的体积为( )
A. B. C. D.
【答案】C
【解析】
如图,设正方形的中点为,正四棱锥的外接球心为,
底面正方形的边长为,,
正四棱锥的体积为,,
则,,
在中由勾股定理可得:,解得,,故选C.
9.如图,在中,,,点为的中点,将沿折起到的位置,使,连接,得到三棱锥.若该三棱锥的所有顶点都在同一球面上,
则该球的表面积是( )
A. B. C. D.
【答案】A
【解析】由题意得该三棱锥的面是边长为的正三角形,且平面,
设三棱锥外接球的球心为,
外接圆的圆心为,则面,∴四边形为直角梯形,
由,,及,得,∴外接球半径为,
∴该球的表面积.故选A.
10.四面体中,,,,则此四面体外接球的表面积为( )
A. B. C. D.
【答案】A
【解析】
由题意,中,,,可知是等边三角形,,
∴的外接圆半径,,
∵,可得,可得,∴,∴,
∴四面体高为.
设外接球,为球心,,可得:……①,
……②
由①②解得:.四面体外接球的表面积:.故选A.
11.将边长为2的正沿着高折起,使,若折起后四点都在球的表面上,则球的表面积为( )
A. B. C. D.
【答案】B
【解析】中,,,,
底面三角形的底面外接圆圆心为,半径为,由余弦定理得到,再由正弦定理得到,
见图示:
是球的弦,,将底面的圆心平行于竖直向上提起,提起到
的高度的一半,即为球心的位置,∴,在直角三角形中,应用勾股定理得到,即为球的半径.
∴球的半径.该球的表面积为;故选B.
12.在三棱锥中,,,则该三棱锥的外接球的表面积为( )
A. B. C. D.
【答案】D
【解析】分别取,的中点,,连接相应的线段,,,
由条件,,,可知,与,都是等腰三角形,
平面,∴,同理,∴是与的公垂线,
球心在上,推导出,可以证明为中点,
,,,
∴,球半径,∴外接球的表面积为.
故选D.
二、填空题
13.棱长均为6的直三棱柱的外接球的表面积是_________.
【答案】
【解析】由正弦定理可知底面三角形的外接圆半径为,
则外接球的半径,
则外接球的表面积为.
14.已知棱长都相等正四棱锥的侧面积为,则该正四棱锥内切球的表面积为________.
【答案】
【解析】设正四棱锥的棱长为,则,解得.
于是该正四棱锥内切球的大圆是如图的内切圆,
其中,.∴.
设内切圆的半径为,由,得,即,
解得,
∴内切球的表面积为.
15.已知三棱柱的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为,,,,则此球的表面积等于______.
【答案】
【解析】∵三棱柱的侧棱垂直于底面,棱柱的体积为,,,,,,
,,
设外接圆的半径为,则,,
∴外接球的半径为,∴球的表面积等于.故答案为.
16.在三棱锥中,,,,,则三棱锥外接球的体积的最小值为_____.
【答案】
【解析】如图所示,三棱锥的外接圆即为长方体的外接圆,外接圆的直径为长方体的体对角线,
设,那么,,所以.由题意,体积的最小值即为
最小,,所以当时,的最小值为,所以半径为,
故体积的最小值为.
相关文档
- 2019年高考数学练习题汇总填空题满2021-06-196页
- 2019年高考数学练习题汇总高考填空2021-06-196页
- 2019年高考数学练习题汇总填空题满2021-06-195页
- 2019年高考数学练习题汇总小题提速2021-06-197页
- 2019年高考数学练习题汇总10+7满分2021-06-197页
- 2019年高考数学练习题汇总10+7满分2021-06-176页
- 2019年高考数学练习题汇总高考模拟2021-06-1615页
- 2019年高考数学练习题汇总(七)计数2021-06-163页
- 2019年高考数学练习题汇总高考解答2021-06-167页
- 2019年高考数学练习题汇总小题提速2021-06-166页