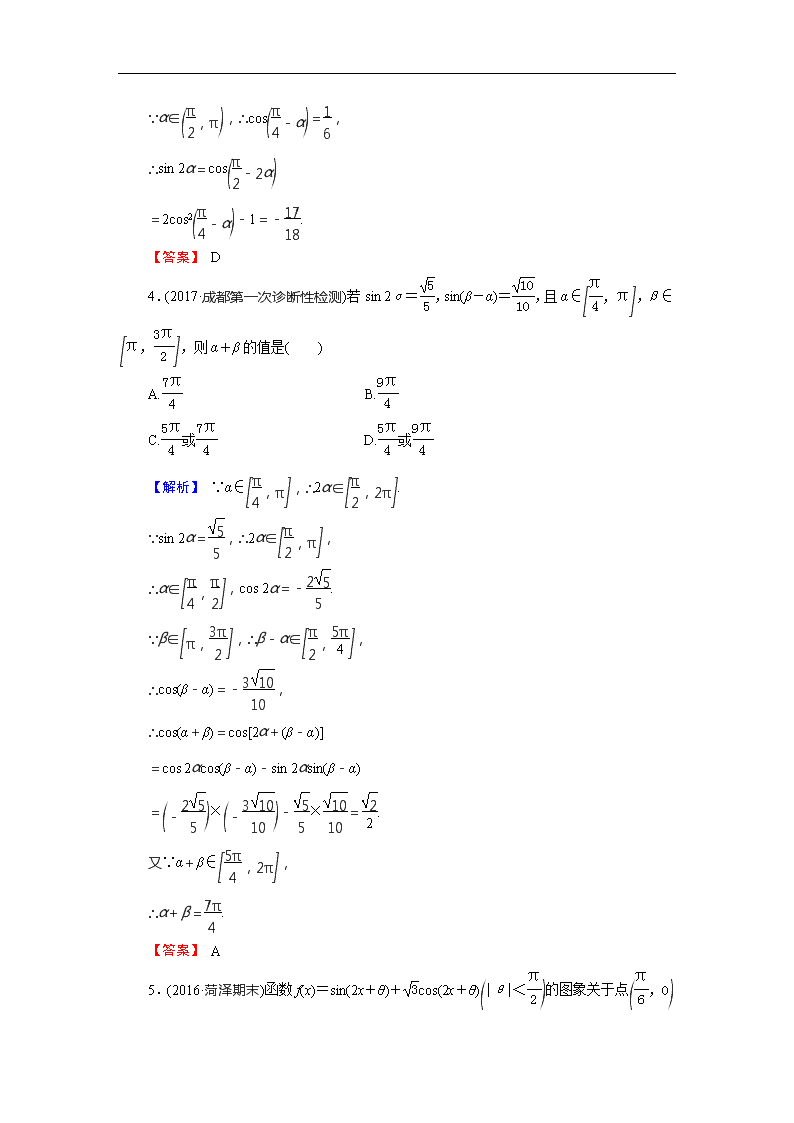高考数学专题复习练习：4-6 专项基础训练 8页

‎ A组　专项基础训练 ‎(时间：30分钟)‎ ‎1．(2015·陕西)“sin α＝cos α”是“cos 2α＝0”的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎【解析】 sin α＝cos α⇒cos 2α＝cos2α－sin2α＝0；‎ cos 2α＝0⇔cos α＝±sin α⇒/ sin α＝cos α，故选A.‎ ‎【答案】 A ‎2．(2016·山东)函数f(x)＝(sin x＋cos x)(cos x－sin x)的最小正周期是(　　)‎ A.　　　　　　　　　　　B．π C. D．2π ‎【解析】 ∵f(x)＝(sin x＋cos x)(cos x－sin x)＝4sin·cos＝2sin，∴T＝＝π，故选B.‎ ‎【答案】 B ‎3．若α∈，且3cos 2α＝sin，则sin 2α的值为(　　)‎ A. B．－ C. D．－ ‎【解析】 cos 2α＝sin＝sin ‎＝2sincos 代入原式，得 ‎6sincos＝sin，‎ ‎∵α∈，∴cos＝，‎ ‎∴sin 2α＝cos ‎＝2cos2－1＝－.‎ ‎【答案】 D ‎4．(2017·成都第一次诊断性检测)若sin 2α＝，sin(β－α)＝，且α∈，β∈，则α＋β的值是(　　)‎ A. B. C.或 D.或 ‎【解析】 ∵α∈，∴2α∈.‎ ‎∵sin 2α＝，∴2α∈，‎ ‎∴α∈，cos 2α＝－.‎ ‎∵β∈，∴β－α∈，‎ ‎∴cos(β－α)＝－，‎ ‎∴cos(α＋β)＝cos[2α＋(β－α)]‎ ‎＝cos 2αcos(β－α)－sin 2αsin(β－α)‎ ‎＝×－×＝.‎ 又∵α＋β∈，‎ ‎∴α＋β＝.‎ ‎【答案】 A ‎5．(2016·菏泽期末)函数f(x)＝sin(2x＋θ)＋cos(2x＋θ)的图象关于点对称，则f(x)的单调递增区间为(　　)‎ A.，k∈Z B.，k∈Z C.，k∈Z D.，k∈Z ‎【解析】 ∵f(x)＝sin(2x＋θ)＋cos(2x＋θ)‎ ‎＝2sin，‎ 由题意知2×＋θ＋＝kπ(k∈Z)，‎ ‎∴θ＝kπ－π(k∈Z)．‎ ‎∵|θ|＜，∴θ＝.‎ ‎∴f(x)＝2sin.‎ 由2kπ－≤2x＋π≤2kπ＋(k∈Z)，‎ 得kπ－π≤x≤kπ－(k∈Z)．故选C.‎ ‎【答案】 C ‎6．已知tan＝3，则sin 2θ－2cos2θ的值为________．‎ ‎【解析】 ∵tan＝3，‎ ‎∴＝3，解得tan θ＝.‎ ‎∴sin 2θ－2cos2θ ‎＝ ‎＝ ‎＝＝－.‎ ‎【答案】 － ‎7．(2016·浙江卷)已知2cos2x＋sin 2x＝Asin(ωx＋φ)＋b(A＞0)，则A＝________，b＝________．‎ ‎【解析】 由于2cos2x＋sin 2x＝1＋cos 2x＋sin 2x ‎＝sin＋1，所以A＝，b＝1.‎ ‎【答案】 　1‎ ‎8．(2015·北京西城一模)若锐角α，β满足(1＋tan α)(1＋tan β)＝4，则α＋β＝________．‎ ‎【解析】 因为(1＋tan α)(1＋tan β)＝4，‎ 所以1＋(tan α＋tan β)＋3tan αtan β＝4，‎ 即(tan α＋tan β)＝3－3tan αtan β＝3(1－tan αtan β)，‎ 即tan α＋tan β＝(1－tan αtan β)．‎ ‎∴tan(α＋β)＝＝.‎ 又∵α，β为锐角，∴α＋β＝.‎ ‎【答案】 ‎9．(2016·沈阳质检)已知函数f(x)＝2sin xsin.‎ ‎(1)求函数f(x)的最小正周期和单调递增区间；‎ ‎(2)当x∈时，求函数f(x)的值域．‎ ‎【解析】 (1)f(x)＝2sin x＝×＋sin 2x＝sin＋.‎ 所以函数f(x)的最小正周期为T＝π.‎ 由－＋2kπ≤2x－≤＋2kπ，k∈Z，‎ 解得－＋kπ≤x≤＋kπ，k∈Z，‎ 所以函数f(x)的单调递增区间是，k∈Z.‎ ‎(2)当x∈时，2x－∈，‎ sin∈，‎ f(x)∈.‎ 故f(x)的值域为.‎ B组　专项能力提升 ‎(时间：20分钟)‎ ‎10．设α∈，β∈，且tan α＝，则(　　)‎ A．3α－β＝ B．2α－β＝ C．3α＋β＝ D．2α＋β＝ ‎【解析】 由tan α＝得＝，‎ 即sin αcos β＝cos α＋cos αsin β，‎ ‎∴sin(α－β)＝cos α＝sin.‎ ‎∵α∈，β∈，‎ ‎∴α－β∈，－α∈，‎ 由sin(α－β)＝sin，得α－β＝－α，‎ ‎∴2α－β＝.‎ ‎【答案】 B ‎11．定义运算＝ad－bc，若cos α＝，＝，0＜β＜α＜，则β等于(　　)‎ A. B. C. D. ‎【解析】 依题意有sin αcos β－cos αsin β＝sin(α－β)＝，‎ 又0＜β＜α＜，∴0＜α－β＜，‎ 故cos(α－β)＝＝，‎ 而cos α＝，∴sin α＝，‎ 于是sin β＝sin[α－(α－β)]‎ ‎＝sin αcos(α－β)－cos αsin(α－β)‎ ‎＝×－×＝，‎ 故β＝，故选D.‎ ‎【答案】 D ‎12．(2017·河南百校联盟教学质量监测)已知函数f(x)＝|sin x|＋|cos x|，则下列结论中错误的是(　　)‎ A．f(x)是周期函数 B．f(x)图象的对称轴方程为x＝，k∈Z C．f(x)在区间上为增函数 D．方程f(x)＝在区间上有6个根 ‎【解析】 因为f＝＋＝|sin x|＋|cos x|＝f(x)，所以f(x)是周期为的函数．因为f(x)为偶函数，所以f(x)图象的对称轴方程为x＝，k∈Z，故A，B项正确．当x∈时，f(x)＝sin x＋cos x＝sin，作出函数f(x)的部分图象如图所示，由图象可知C项错误，D项正确．‎ ‎【答案】 C ‎13．设x∈，则函数y＝的最小值为________．‎ ‎【解析】 方法一 因为y＝＝，‎ 所以令k＝.又x∈，‎ 所以k就是单位圆x2＋y2＝1的左半圆上的动点 P(－sin 2x，cos 2x)与定点Q(0，2)所成直线的斜率．‎ 又kmin＝tan 60°＝，‎ 所以函数y＝的最小值为.‎ 方法二 y＝＝ ‎＝＝tan x＋.‎ ‎∵x∈，∴tan x＞0.‎ ‎∴tan x＋≥2 ＝.‎ 即函数的最小值为.‎ ‎【答案】 ‎14．(2016·临沂一模)已知函数f(x)＝2cos2ωx－1＋2cos ωxsin ωx(0＜ω＜1)，直线x＝是f(x)图象的一条对称轴．‎ ‎(1)试求ω的值；‎ ‎(2)已知函数y＝g(x)的图象是由y＝f(x)图象上各点的横坐标伸长到原来的2倍，然后再向左平移个单位长度得到的，若g＝，α∈，求sin α的值．‎ ‎【解析】 f(x)＝2cos2ωx－1＋2cos ωxsin ωx ‎＝cos 2ωx＋sin 2ωx ‎＝2sin.‎ ‎(1)由于直线x＝是函数f(x)＝2sin图象的一条对称轴，‎ ‎∴sin＝±1.‎ ‎∴ω＋＝kπ＋(k∈Z)，‎ ‎∴ω＝k＋(k∈Z)．‎ 又0＜ω＜1，∴－＜k＜.‎ 又∵k∈Z，从而k＝0，∴ω＝.‎ ‎(2)由(1)知f(x)＝2sin，‎ 由题意可得 g(x)＝2sin，‎ 即g(x)＝2cosx，‎ ‎∵g＝2cos＝，‎ ‎∴cos＝.‎ 又α∈，‎ ‎∴＜α＋＜，‎ ‎∴sin＝.‎ ‎∴sin α＝sin ‎＝sincos－cossin ‎＝×－×＝.‎