2005年浙江省高考数学试卷（文科）【附答案、word版本，可再编辑；B4纸型两栏】 7页

‎2005年浙江省高考数学试卷（文科）‎ 一、选择题（共10小题，每小题5分，满分50分）‎ ‎1. 函数y=sin(‎1‎‎2‎x+3)‎的最小正周期是（ ）‎ A.π‎2‎ B.π C.‎2π D.‎‎4π ‎2. 设全集U={1, 2, 3, 4, 5, 6, 7}‎，P={1, 2, 3, 4, 5}‎，Q={3, 4, 5, 6, 7}‎，则P∩(‎∁‎UQ)=(‎ ‎‎)‎ A.‎{1, 2}‎ B.‎{3, 4, 5}‎ C.‎{1, 2, 6, 7}‎ D.‎‎{1, 2, 3, 4, 5}‎ ‎3. 点‎(1, -1)‎到直线x-y+1‎＝‎0‎的距离是（ ）‎ A.‎1‎‎2‎ B.‎3‎‎2‎ C.‎2‎‎2‎ D.‎‎3‎‎2‎‎2‎ ‎4. 设f(x)=|x-1|-|x|‎，则f[f(‎1‎‎2‎)]=(‎        ‎‎)‎ A.‎-‎‎1‎‎2‎ B.‎0‎ C.‎1‎‎2‎ D.‎‎1‎ ‎5. 在‎(1+x‎)‎‎5‎-(1+x‎)‎‎4‎的展开式中，含x‎3‎的项的系数是（ ）‎ A.‎-5‎ B.‎5‎ C.‎6‎ D.‎‎10‎ ‎6. 从存放号码分别为‎1‎，‎2‎，…，‎10‎的卡片的盒子中，有放回地取‎100‎次，每次取一张卡片并记下号码．统计结果如图，则取到号码为奇数的频率是（ ）‎ 卡片号码 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 取到的次数 ‎13‎ ‎8‎ ‎5‎ ‎7‎ ‎6‎ ‎13‎ ‎18‎ ‎10‎ ‎11‎ ‎9‎ A.‎0.53‎ B.‎0.5‎ C.‎0.47‎ D.‎‎0.37‎ ‎7. 设α，β为两个不同的平面，l，m为两条不同的直线，且l⊂α，m⊂β，有如下的两个命题：①若α // β，则l // m；②若l⊥m，则α⊥β.那么（        ）‎ A.①是真命题，②是假命题 B.①是假命题，②是真命题 C.①②都是真命题 D.①②都是假命题 ‎8. 已知向量a‎→‎‎=(x-5,3)‎，b‎→‎‎=(2,x)‎，且a‎→‎‎⊥‎b‎→‎，则由x的值构成的集合是（ ）‎ A.‎{2, 3}‎ B.‎{-1, 6}‎ C.‎{2}‎ D.‎‎{6}‎ ‎9. 函数y=ax‎2‎+1‎的图象与直线y=x相切，则a=(‎ ‎‎)‎ A.‎1‎‎8‎ B.‎1‎‎4‎ C.‎1‎‎2‎ D.‎‎1‎ ‎10. 设集合A={(x, y)|x, y, 1-x-y是三角形的三边长‎}‎，则A所表示的平面区域（不含边界的阴影部分）是‎(‎        ‎‎)‎ A. B. ‎ C. D. ‎ 二、填空题（共4小题，每小题4分，满分16分）‎ ‎11. 函数y=xx+2‎(x∈R，且x≠-2)‎的反函数是________．‎ ‎12. 设M、N是直角梯形ABCD两腰的中点，DE⊥AB于E（如图）、现将‎△ADE沿DE折起，使二面角A-DE-B为‎45‎‎∘‎，此时点A在平面BCDE内的射影恰为点B ‎ 7 / 7‎ ‎，则M、N的连线与AE所成角的大小等于________．‎ ‎13. 过双曲线x‎2‎a‎2‎‎-y‎2‎b‎2‎=1(a>0, b>0)‎的左焦点且垂直于x轴的直线与双曲线相交于M、N两点，以MN为直径的圆恰好过双曲线的右顶点，则双曲线的离心率等于________．‎ ‎14. 从集合‎{P, Q, R, S}‎与‎{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}‎中各任取‎2‎个元素排成一排（字母和数字均不能重复）、每排中字母Q和数字‎0‎至多只能出现一个的不同排法种数是________．（用数字作答）、‎ 三、解答题（共6小题，满分84分）‎ ‎15. 已知函数f(x)=2sinxcosx+cos2x ‎（1）求f(π‎4‎)‎的值；‎ ‎（2）设α∈(0, π)‎，f(α‎2‎)=‎‎2‎‎2‎，求sinα的值、‎ ‎16. 已知实数a，b，c成等差数列，a+1‎，b+1‎，c+4‎成等比数列，且a+b+c=15‎，求a，b，‎c ‎17. 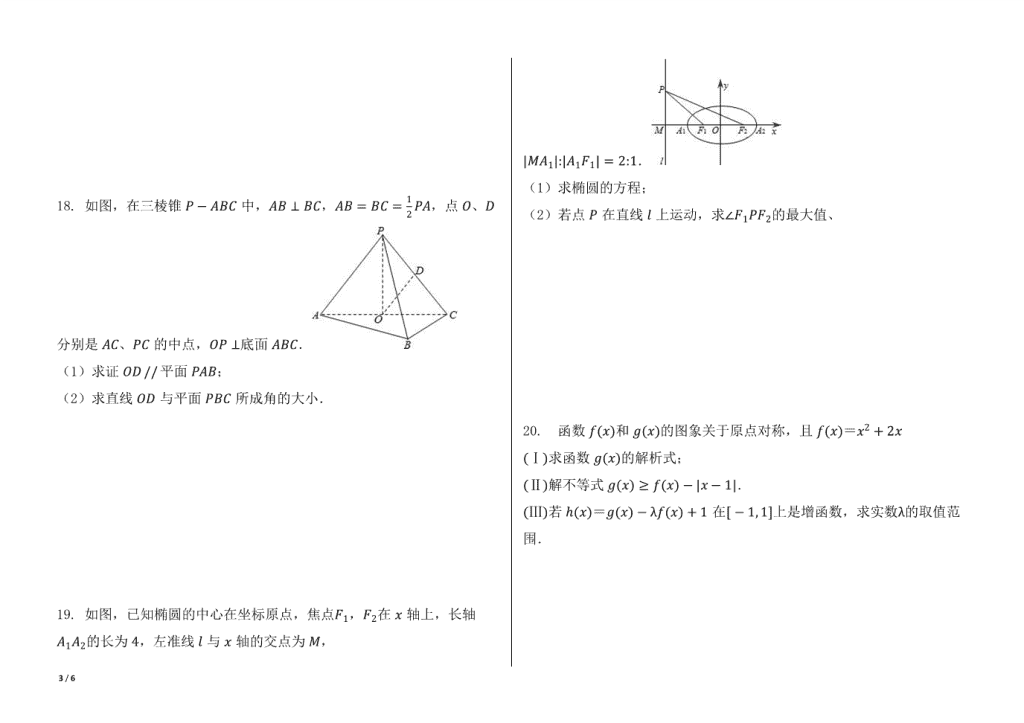袋子A和B中装有若干个均匀的红球和白球，从A中摸出一个红球的概率是‎1‎‎3‎，从B中摸出一个红球的概率为p．‎ ‎（1）从A中有放回地摸球，每次摸出一个，有‎3‎次摸到红球即停止．‎ ‎(I)‎求恰好摸‎5‎次停止的概率；‎ ‎（2）记‎5‎次之内（含‎5‎次）摸到红球的次数为ξ，求随机变量ξ的分布率及数学期望Eξ．‎ ‎(II)‎若A、B两个袋子中的球数之比为‎1:2‎，将A、B中的球装在一起后，从中摸出一个红球的概率是‎2‎‎5‎，求p的值．‎ ‎ 7 / 7‎ ‎18. 如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=‎1‎‎2‎PA，点O、D分别是AC、PC的中点，OP⊥‎底面ABC．‎ ‎（1）求证OD // ‎平面PAB；‎ ‎（2）求直线OD与平面PBC所成角的大小．‎ ‎19. 如图，已知椭圆的中心在坐标原点，焦点F‎1‎，F‎2‎在x轴上，长轴A‎1‎A‎2‎的长为‎4‎，左准线l与x轴的交点为M，‎|MA‎1‎|:|A‎1‎F‎1‎|=2:1‎．‎ ‎（1）求椭圆的方程；‎ ‎（2）若点P在直线l上运动，求‎∠F‎1‎PF‎2‎的最大值、‎ ‎20. 函数f(x)‎和g(x)‎的图象关于原点对称，且f(x)‎＝‎x‎2‎‎+2x ‎(‎Ⅰ‎)‎求函数g(x)‎的解析式；‎ ‎(‎Ⅱ‎)‎解不等式g(x)≥f(x)-|x-1|‎．‎ ‎(‎Ⅲ‎)‎若h(x)‎＝g(x)-λf(x)+1‎在‎[-1, 1]‎上是增函数，求实数λ的取值范围．‎ ‎ 7 / 7‎ 参考答案与试题解析 ‎2005年浙江省高考数学试卷（文科）‎ 一、选择题（共10小题，每小题5分，满分50分）‎ ‎1.D ‎2.A ‎3.D ‎4.D ‎5.C ‎6.A ‎7.D ‎8.C ‎9.B ‎10.A 二、填空题（共4小题，每小题4分，满分16分）‎ ‎11.‎y=‎2x‎1-x(x∈R，且x≠1)‎ ‎12.‎‎90‎‎∘‎ ‎13.‎‎2‎ ‎14.‎‎5832‎ 三、解答题（共6小题，满分84分）‎ ‎15.解：（1）∵ ‎f(x)=sin2x+cos2x ‎∴ ‎f(π‎4‎)=sinπ‎2‎+cosπ‎2‎=1‎ ‎（2）‎f(α‎2‎)=cosα+sinα=‎‎2‎‎2‎ ‎∴ sin(α+π‎4‎)=‎1‎‎2‎，cos(α+π‎4‎)=±‎‎3‎‎2‎．sinα=sin(α+π‎4‎-π‎4‎)=‎1‎‎2‎×‎2‎‎2‎∓‎3‎‎2‎×‎2‎‎2‎=‎‎2‎‎∓‎‎6‎‎4‎．‎ ‎∵ α∈(0, π)‎，∴ sinα>0‎，故sinα=‎‎2‎‎+‎‎6‎‎4‎ ‎16.解：由题意，得a+b+c=15(1)‎a+c=2b(2)‎‎(a+1)(c+4)=(b+1‎)‎‎2‎(3)‎ 由‎(1)(2)‎两式，解得b=5‎ 将c=10-a代入‎(3)‎，整理得a‎2‎‎-13a+22=0‎ 解得a=2‎或a=11‎，‎ 故a=2‎，b=5‎，c=8‎或a=11‎，b=5‎，c=-1‎．‎ 经验算，上述两组数符合题意．‎ ‎17.解：‎(1)(I)‎由题意知本题是在相同的条件下进行的试验，且事件发生的概率相同，可以看作独立重复试验，恰好摸‎5‎次停止表示第五次一定摸到红球，前四次有两次摸到红球，根据独立重复试验公式得到 ‎ ‎ ‎ξ ‎ ‎‎0‎ ‎1‎‎ ‎ ‎2‎‎ ‎ ‎3‎‎ ‎ ‎ ‎P ‎ ‎‎32‎‎243‎ ‎ ‎‎80‎‎243‎ ‎ ‎‎80‎‎243‎ ‎ ‎‎17‎‎243‎ C‎4‎‎2‎‎×(‎1‎‎3‎‎)‎‎2‎×(‎2‎‎3‎‎)‎‎2‎×‎1‎‎3‎=‎‎8‎‎81‎‎．‎ ‎（2）由题意知从A中有放回地摸球，每次摸出一个，有‎3‎次摸到红球即停止 ‎∴ 随机变量ξ的取值为‎0‎，‎1‎，‎2‎，‎3‎；‎ ‎ 7 / 7‎ 由n次独立重复试验概率公式Pn‎(k)=Cnkpk(1-p‎)‎n-k，得 P(ξ=0)=C‎5‎‎0‎×(1-‎1‎‎3‎‎)‎‎5‎=‎‎32‎‎243‎‎；‎ P(ξ=1)=C‎5‎‎1‎×‎1‎‎3‎×(1-‎1‎‎3‎‎)‎‎4‎=‎‎80‎‎243‎‎；‎ P(ξ=2)=C‎5‎‎2‎×(‎1‎‎3‎‎)‎‎2‎×(1-‎1‎‎3‎‎)‎‎3‎=‎‎80‎‎243‎‎；‎ P(ξ=3)=C‎3‎‎3‎(‎1‎‎3‎‎)‎‎3‎+C‎3‎‎2‎⋅(‎1‎‎3‎‎)‎‎2‎⋅‎2‎‎3‎⋅‎1‎‎3‎+C‎4‎‎2‎(‎1‎‎3‎‎)‎‎2‎(‎2‎‎3‎‎)‎‎2‎⋅‎1‎‎3‎=‎‎17‎‎81‎‎．‎ 随机变量ξ的分布列是 ‎∴ ξ的数学期望是Eξ=‎32‎‎243‎×0+‎80‎‎243‎×1+‎80‎‎243‎×2+‎51‎‎243‎×3=‎‎131‎‎81‎．‎ ‎（2）由题意知本题是一个古典概型，‎ 设袋子A中有m个球，则袋子B中有‎2m个球．‎ 试验发生的所有事件是‎3m，‎ 而满足条件的是‎1‎‎3‎m+2mp，‎ 根据古典概型公式得到 ‎1‎‎3‎m+2mp‎3m‎=‎‎2‎‎5‎‎，‎ ‎∴ p=‎‎13‎‎30‎．‎ ‎18.解：方法一：（1）∵ O、D分别为AC、PC中点，‎ ‎∴ OD // PA又PA⊂‎平面PAB ‎∴ OD // ‎平面PAB ‎（2）∵ AB⊥BC，OA=OC，∴ OA=OB=OC，‎ 又∵ OP⊥‎平面ABC ‎∴ PA=PB=PC．取BC中点E，连接PE，则BC⊥‎平面POE作OF⊥PE于F，连接DF，则OF⊥‎平面PBC ‎∴ ‎∠ODF是OD与平面PBC所成的角．‎ 可设PA=2‎，AB=BC=1‎，PO=‎‎14‎‎2‎，EO=‎‎1‎‎2‎，PE=‎‎15‎‎2‎，‎ OD=1‎‎，OF=PO⋅EOPE=‎‎14‎‎2‎‎15‎，‎ 在Rt△ODF中，sin∠ODF=OFOD=‎‎210‎‎30‎，‎ ‎∴ OD与平面PBC所成的角为arcsin‎210‎‎30‎．‎ 方法二：∵ OP⊥‎平面ABC，OA=OC，AB=BC，‎ ‎∴ OA⊥OB，OA⊥OP，OB⊥OP．以O为原点，射线OP为非负z轴，建立空间直角坐标系O-xyz（如图），‎设AB=a，则A(‎2‎‎2‎a,0,0)，B(0,‎2‎‎2‎a,0)，C(-‎2‎‎2‎a,0,0)‎ 设OP=h，则P(0, 0, h)‎．‎ ‎（1）∵ D为PC的中点，‎ ‎ 7 / 7‎ ‎∴ OD‎→‎‎=(-‎2‎‎4‎a,0,‎1‎‎2‎h)，又PA‎→‎=(‎2‎‎2‎a,0,-h)‎，‎ ‎∴ OD‎→‎‎=-‎‎1‎‎2‎PA‎→‎．∴ OD‎→‎‎ // ‎PA‎→‎．∴ OD // ‎平面PAB．‎ ‎（2）∵ PA=2a∴ h=‎7‎‎2‎a，‎ ‎∴ OD‎→‎‎=(-‎2‎‎4‎a,0,‎14‎‎4‎a)‎，可求得平面PBC的法向量n‎→‎‎=(-1,1,‎1‎‎7‎)‎，‎ ‎∴ cos⟨OD‎→‎，n‎→‎>=‎|OD‎→‎|⋅|n‎→‎|‎‎˙‎=‎‎210‎‎30‎．‎ 设OD与平面PBC所成的角为θ，‎ 则sinθ=|cos⟨OD‎→‎，n‎→‎>|=‎‎210‎‎30‎，‎ ‎∴ OD与平面PBC所成的角为arcsin‎210‎‎30‎ ‎19.解：（1）设椭圆方程为x‎2‎a‎2‎‎+y‎2‎b‎2‎=1(a>b>0)‎，半焦距为c，‎ 则‎|MA‎1‎|=a‎2‎c-a，|A‎1‎F‎1‎|=a-c由题意，‎ 得a‎2‎c‎-a=2(a-c)‎‎2a=4‎a‎2‎‎=b‎2‎+‎c‎2‎，∴ a=2‎，b=‎‎3‎，c=1‎，故椭圆方程为x‎2‎‎4‎‎+y‎2‎‎3‎=1‎．‎ ‎（2）设P(-4, y‎0‎)‎，y‎0‎‎≠0‎设直线PF‎1‎的斜率k‎1‎‎=-‎y‎0‎‎3‎，直线PF‎2‎的斜率k‎2‎‎=-‎y‎0‎‎5‎，‎ ‎∵ ‎0<∠F‎1‎PF‎2‎<∠PF‎1‎M<‎π‎2‎，∴ ‎∠F1PF为锐角．‎ ‎∴ tan∠F‎1‎PF‎2‎=|k‎2‎‎-‎k‎1‎‎1+‎k‎1‎k‎2‎|=‎2|y‎0‎|‎y‎0‎‎2‎‎+15‎≤‎2|y‎0‎|‎‎2‎15‎|y‎0‎|‎=‎‎15‎‎15‎．‎ 当‎|y‎0‎|=‎‎15‎，即y‎0‎‎=±‎‎15‎时，tan∠F‎1‎PF‎2‎取到最大值，‎ 此时‎∠F‎1‎PF‎2‎最大，故‎∠F‎1‎PF‎2‎的最大值为arctan‎15‎‎15‎．‎ ‎20.（1）设函数y＝f(x)‎的图象上任意一点Q(x‎0‎, y‎0‎)‎关于原点的对称点为P(x, y)‎，‎ 则x‎0‎‎+x‎2‎‎=0‎y‎0‎‎+y‎2‎‎=0‎‎ ‎即x‎0‎‎=-xy‎0‎‎=-y.‎ ‎∵ 点Q(x‎0‎, y‎0‎)‎在函数y＝f(x)‎的图象上 ‎∴ ‎-y＝x‎2‎‎-2x，即y＝‎-x‎2‎+2x，故g(x)‎＝‎‎-x‎2‎+2x ‎（2）由g(x)≥f(x)-|x-1|‎，可得‎2x‎2‎-|x-1|≤0‎ 当x≥1‎时，‎2x‎2‎-x+1≤0‎，此时不等式无解．‎ 当x<1‎时，‎2x‎2‎+x-1≤0‎，解得‎-1≤x≤‎‎1‎‎2‎．‎ 因此，原不等式的解集为‎[-1,‎1‎‎2‎]‎．‎ ‎(‎Ⅲ‎)h(x)‎＝‎‎-(1+λ)x‎2‎+2(1-λ)x+1‎ ‎①当λ＝‎-1‎时，h(x)‎＝‎4x+1‎在‎[-1, 1]‎上是增函数，∴ λ＝‎‎-1‎ ‎②当λ≠-1‎时，对称轴的方程为x=‎‎1-λ‎1+λ．‎ ‎ 7 / 7‎ ⅰ）当λ<-1‎时，‎1-λ‎1+λ‎≤-1‎，解得λ<-1‎．‎ ⅱ）当λ>-1‎时，‎1-λ‎1+λ‎≥1‎，解得‎-1<λ≤0‎．综上，λ≤0‎．‎ ‎ 7 / 7‎