高考数学模拟试卷 2 (16) 11页

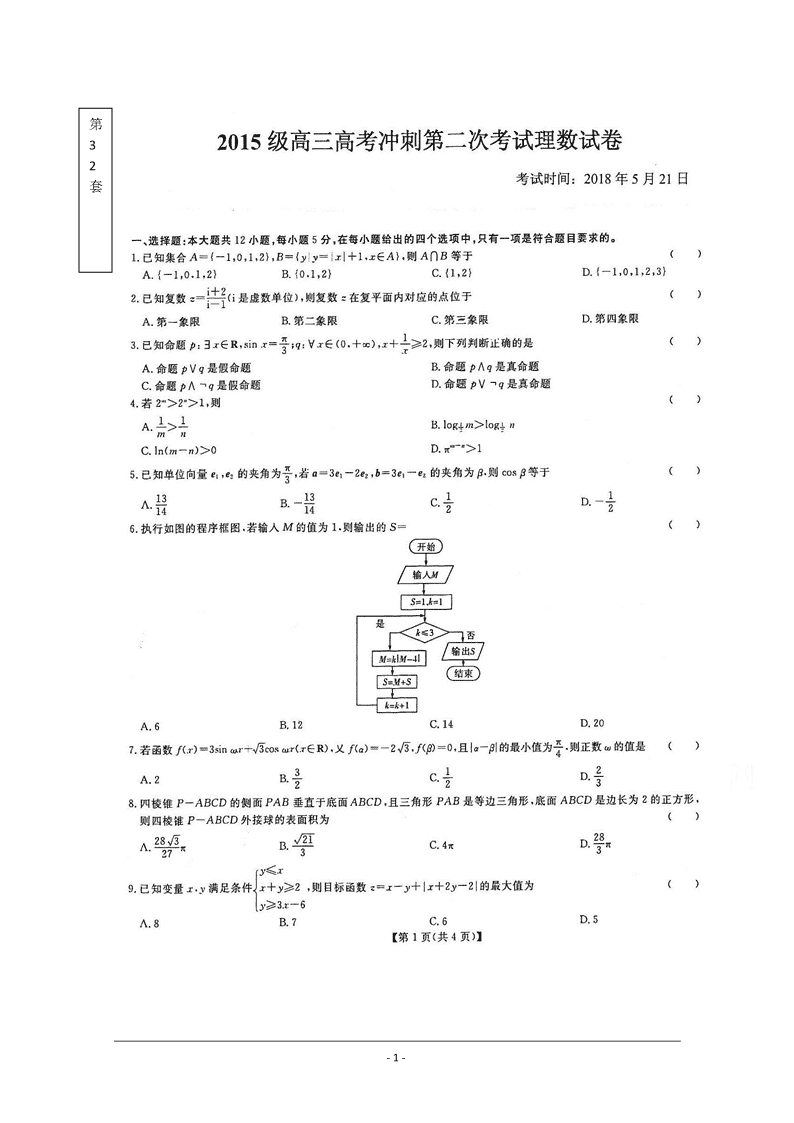
- 1 - 第 3 2 套 - 2 - - 3 - - 4 - - 5 - z y x 第 18 题图 P A B D O 理科数学答案（32） B CCDA BADBC BA 10. C 【解析】相当于将砝码分成了十一个小组，第i 组有i 个i 克砝码。若从i 组中不取砝码相当 于 1，若从i 组中取一个砝码有 i 种取法，相当于 iix 。所以选 C 11．B 12． A 【解析】由题意可知 32)]()([  xexfxf x ，即 32])([  xexf x ，所以 Cxxexf x  3)( 2 ， xexxxff  )13()(,1)0( 2 ，由 )(xf 的图像可以知道 13. 1 14. 3 311201620171 1 2 2016 2017 2017 2018 2018  abbbaa a a a a aa  15. 24 16. 7 34 ；因为 )(xf 是奇函数，所以四边形的对角线交于坐标原点， ABCD 的面积为三角形 OAB 的四倍， 17.（【解析】（1）当 1 11, 13; 2 , 2 15n n nn S n n Z a S S n        且 …………4 分 所以 =2 15na n  ……………………….6 分 （2） 7 8 17 , 7, ,n nn a a n a a  当 时， 异号； 同号 20 1 2 6 7 7 8 20 21 1 2 20 21 7 8 1 21 1 1 1 1= 1 1 2 1 1 1( ) 22 682 351 T a a a a a a a a a a a a a a a a                 18. 【解析】（Ⅰ）证明：  BCAD// ， BCAB  ， 2BC AB  ， 3AD . 5 10 5OC OD CD   ， ， - 6 - 2 2 2OD OC DC  OC CD  CD POC  平面 CD PO   ABPBPA  ， O 为 AB 中点  ABPO   PO 底面 ABCD  平面 PAB 面 ABCD……………6 分 （ Ⅱ ） 如 图 建 立 空 间 直 角 坐 标 系 xyzO  ， 则 )3,0,0(P ， )0,3,1(D ， )0,2,1(C  (0,0, 3), ( 1,3,0), ( 1, 2, 3), ( 2,1,0) OP OD CP CD             设平面OPD 的一个法向量为 ),,( 111 zyxm  ， 平面 PCD 的法向量为 ),,( 222 zyxn  则 由      0 0 mOD mOP 可得      03 03 11 1 yx z ，取 11 y ，得 31 x ， 01 z ，即 )0,1,3(m ， 由      0 0 nCD nCP 可得      02 032 22 222 yx zyx ，取 32 x ，得 322 y ， 52 z ， 即 )5,32,3(n  4 3 4010 35,cos  nm nmnm 故二面角 CPDO  的余弦值为 4 3 .……………12 分 19. 【解析】：（Ⅰ）在区间[30，60）的频率为 7 3 364 156  ---------1 分 3 1= =7 30 70 频率 组距 ， ----2 分 设在区间[0，30）上， a频率 组距 ，则 130)210 1 105 1 70 1( a ，解得 210 1a ，-----3 分 补充频率分布直方图如右图； ----------------------------6 分 （Ⅱ）记水电站日利润为 Y 元．由（Ⅰ）知：不能运行发电机的概率为 7 1 ，恰好运行一台发 - 7 - 电机的概率为 7 3 ，恰好运行二台发电机的概率为 7 2 ，恰好运行三台发电机的概率为 7 1 ， ①若安装 1 台发电机，则 Y 的值为-500，4000，其分布列为 E(Y)＝ 7 23500 7 640007 1500  ；----------8 分 ②若安装 2 台发电机，则 Y 的值为-1000，3500，8000，其分布列为 Y -1000 3500 8000 P 7 1 7 3 7 3 E(Y)＝ 1 3 3 335001000 3500 80007 7 7 7        ；---------10 分 ③若安装 3 台发电机，则 Y 的值为-1500，3000，7500，12000，其分布列为 Y -1500 3000 7500 12000 P 7 1 7 3 7 2 7 1 E(Y)＝ 7 34500 7 1120007 275007 330007 11500  ； ∵ 34500 33500 23500 7 7 7   ∴要使水电站日利润的期望值最大，该水电站应安装 3 台发电机．--------------12 分 20. 【解析】：（1）由 1 2BF F 为等腰直角三角形可得 b c ，直线 1 :BF y x b  被圆 2 2 2x y b  所 截 得 的 弦 长 为 2 ， 所 以 2, 2a b c   ， 所 以 椭 圆 的 方 程 为 2 2 14 2 x y  ……………4 分 （2）若直线 l 的斜率不存在，则 1 3 66 32 2S     若直线 l 的斜率存在，设直线 l 的方程为 y kx m  ，设 1 1 2 2( , ), ( , )A x y B x y ， 则 2 1 2 1 22 2 4 2( 2),1 2 1 2 km mx x x xk k       ， 1 2 1 2 2 2( ) 2 1 2 my y k x x m k       由题意点 O 为 PAC 重 心 ， 设 0 0( , )P x y ， 则 1 2 0 1 2 00, 03 3 x x x y y y     ， 所 以 Y -500 4000 P 7 1 7 6 - 8 - 0 1 2 0 1 22 2 4 2( ) , ( )1 2 1 2 km mx x x y y yk k           ，代入椭圆 2 2 14 2 x y  得 2 2 2 2 2 2 2 2 2 4 2 1 21(1 2 ) (1 2 ) 2 k m m kmk k      ， …………………………………8 分 设坐标原点 O 到直线 l 的距离为 d，则 PAC 的面积 2 1 2 1 22 2 2 2 2 2 2 2 2 2 2 2 1 1 33 1 32 2 21 3 4 2( 2)( ) 42 1 2 1 2 2 2 2(1 2 )3 2 1 2 1 22(1 2 ) 1 2 3 623 2 1 2 22 mS AC d k x x x x m k km m mk k k m mk kk k k                          综上可得 PAC 面积 S 为定值 3 6 2 ……………………………………………12 分 21. 【解析】（Ⅰ）解：易知 ln(ln ) | e | | ln ln | 0af a a a a a     ， 即 ln a 为函数 ( )f x 的一个零点； ………………………（2 分） 当 lnx a≥ 时，有 e 0x a ≥ ，则 ( ) e ( ln )xf x a a x a    ，从而 ( ) e 0xf x a   ≥ ，在[ln )a  ， 上恒成立， 当 lnx a 时，有 e 0x a  ，则 ( ) e ( ln )xf x a a x a    ，从而 ( ) e 0xf x a    在 ( ln )a， 上 恒成立． 综上，函数 ( )f x 在 R 上单调递增，有唯一零点 ln a ． ………………………（5 分） （ Ⅱ ） 证 明 ： 记 1 2( ) ( ) ( )h x f x f x  ， 则 1 2( ) ( ) ( )h x f x f x    ， 当 2 1ln lnx a a≥ 时 ， 1 2 2 1( ) (e ) (e ) 0x xh x a a a a        恒成立；当 1 2ln lna x a  时， 1 2( ) (e ) (e )x xh x a a     ， 令 ( ) 0h x ≥ 得 1 2ln 2 a ax ≥ ；当 1 2ln lnx a a≤ 时， 1 2 1 2( ) ( e ) ( e ) 0x xh x a a a a        恒成 立；可知函数 ( )h x 在区间 1 2ln 2 a a    ， 上单调递减，在区间 1 2ln 2 a a     ， 上单调递增， 则函数 ( )h x 的最小值为 1 2 1 2 1 2 1 2 1 2 1 1 1 1 2 2 2 2ln ln ln ln ln2 2 2 2 2 a a a a a a a a a ah a a a a a a a a                           - 9 - 1 2 1 1 2 2 1 2ln ln ( )ln 2 a aa a a a a a     ，………（8 分） 从而只需证： 1 2 1 1 2 2 1 2 2 1ln ln ( )ln ( )ln 22 a aa a a a a a a a     1 1 2 2 1 2 1 2 1ln ln ( )ln( ) 2 ln 2 0a a a a a a a a a       ， 记 2 1 1 2 2 1 2 1 2 1( ) ln ln ( )ln( ) 2 ln 2g a a a a a a a a a a      ， 则 2 1a a 2 2 1 2 2 1 2( ) 1 ln (1 ln( )) ln ln( ) 0g a a a a a a a          恒成立，从而函数 2( )g a 在 区 间 1( )a  ， 上 单 调 递 减 ， 则 2 1( ) ( )g a g a 1 1 1 1 1 1 1 1 1ln ln ( )ln( ) 2 ln 2a a a a a a a a a      1 1 1 1 12 ln 2 ln 2 2 ln 2 0a a a a a    ． 综上：存在 x  R ，使得 1 2 2 1( ) ( ) ( )ln 2f x f x a a   ． ………………………（12 分） 22.解：（1） 1C 的普通方程为 4)2( 22  yx ， 1C 的极坐标方程为  cos4 ， 2C 的极坐 标方程为 2sin  …………………………………………………………………………4 分 （2）联立 ( 0)    与 1C 的极坐标方程得 22 cos16|| OA 联立 ( 0)    与 2C 的极坐标方程得 2 24 OB sin  222 cos124||||  OBOA ， 0 2a   ∴ )16,4(|||| 22  OBOA ………………………………………………………………………… ……….10 分 23.解析：（1）不等式   1f x x  可化为 2 1 1 0x x x     ≤ 设函数 2 1 1y x x x      ，则 2 3 , 1 ,1 2 4, 2. x x y x x x x        ≤ ≤ . 令 0y ≤ ，解得 2 43 x≤ ≤ ……………………….5 分 （2）   1 2 1 ( 2) 1f x x x x x       ≥ 当且仅当 ( 1)( 2) 0x x  ≤ 即1 2x≤ ≤ 时取等，故 1k  . 假设存在符合条件的整数 ,a b ，则 2 1a b  1 2 (2 )(2 )a b a ba b     44 b a a b    44 8b a a b   ≥ - 10 - 当且仅当 4b a a b  即 1 1,4 2a b  时取等号，所以 1 2 a b  的最小值为 8. 所以，不存在正数 ,a b ,同时满足： 1 22 , 4a b k a b     ……………10 分 - 11 -