高考数学专题复习教案： 函数的单调性与最值 2页

函数的单调性与最值 主标题：函数的单调性与最值 副标题：为学生详细的分析函数的单调性与最值的高考考点、命题方向以及规律总结。‎ 关键词：函数，单调性，最值 难度：3‎ 重要程度：5‎ 考点剖析：‎ ‎1．理解函数的单调性、最大值、最小值及其几何意义．‎ ‎2．会运用函数图象理解和研究函数的单调性.‎ 命题方向：高考对本内容的考查主要有：①利用函数的图象与性质求函数定义域、值域与最值，尤其是考查对数函数的定义域、值域与最值问题；②借助基本初等函数考查函数单调性与奇偶性的应用，尤其是考查含参函数的单调性问题或借助单调性求参数的范围，主要以解答题的形式考查；③求二次函数的解析式、值域与最值，考查二次函数的最值、一元二次方程与不等式的综合应用；④在函数与导数的解答题中，考查指数函数、对数函数的求导、含参函数单调性的讨论、函数的极值或最值的求解等．‎ 规律总结：1．求函数的单调区间：首先应注意函数的单调区间是其定义域的子集；其次掌握一次函数、二次函数等基本初等函数的单调区间．求函数单调区间的常用方法：根据定义、利用图象、单调函数的性质及利用导数的性质．‎ ‎2．复合函数的单调性：对于复合函数y＝f[g(x)]，若t＝g(x)在区间(a，b)上是单调函数，且y＝f(t)在区间(g(a)，g(b))或者(g(b)，g(a))上是单调函数，若t＝g(x)与y＝f(t)的单调性相同(同时为增或减)，则y＝f[g(x)]为增函数；若t＝g(x)与y＝f(t)的单调性相反，则y＝f[g(x)]为减函数．简称：同增异减．‎ ‎3．函数的值域常常化归为求函数的最值问题，要重视函数的单调性在确定函数最值过程中的应用．‎ 知 识 梳 理 ‎1．函数的单调性 ‎(1)单调函数的定义 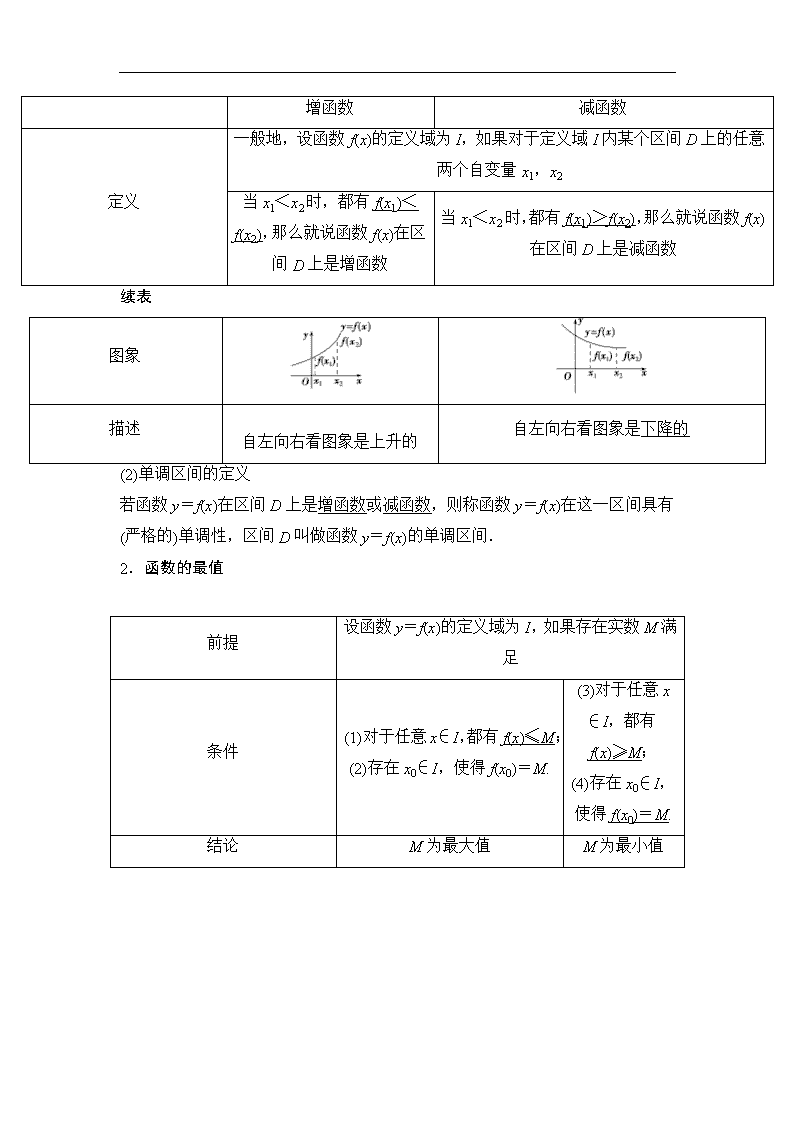增函数 减函数 定义 一般地，设函数f(x)的定义域为I，如果对于定义域I内某个区间D上的任意两个自变量x1，x2‎ 当x1＜x2时，都有f(x1)＜f(x2)，那么就说函数f(x)在区间D上是增函数 当x1＜x2时，都有f(x1)＞f(x2)，那么就说函数f(x)在区间D上是减函数 续表 图象 描述 自左向右看图象是上升的 自左向右看图象是下降的 ‎(2)单调区间的定义 若函数y＝f(x)在区间D上是增函数或减函数，则称函数y＝f(x)在这一区间具有(严格的)单调性，区间D叫做函数y＝f(x)的单调区间．‎ ‎2．函数的最值 前提 设函数y＝f(x)的定义域为I，如果存在实数M满足 条件 ‎(1)对于任意x∈I，都有f(x)≤M；‎ ‎(2)存在x0∈I，使得f(x0)＝M.‎ ‎(3)对于任意x∈I，都有f(x)≥M；‎ ‎(4)存在x0∈I，使得f(x0)＝M.‎ 结论 M为最大值 M为最小值