高考数学专题复习教案： 恒成立问题备考策略 3页

不等式恒成立问题备考策略 主标题：不等式恒成立问题备考策略 副标题：通过考点分析高考命题方向，把握高考规律，为学生备考复习打通快速通道。‎ 关键词：不等式，不等式恒成立，备考策略 难度：3‎ 重要程度：5‎ 内容：‎ 1. 一元二次不等式恒成立 ；‎ 一元二次不等式恒成立 ；‎ 一元二次不等式恒成立 ；‎ 一元二次不等式恒成立 ；‎ 思维规律解题 一、 分离参数 ‎ 例1、已知函数，若对任意恒有，试确定的取值范围。‎ 解：根据题意得：在上恒成立，‎ 即：在上恒成立，‎ 设，则 当时， 所以 ‎ 例2、已知时，不等式恒成立，求的取值范围。‎ 解：令， 所以原不等式可化为：，‎ 要使上式在上恒成立，只须求出在上的最小值即可。‎ ‎ ‎ ‎ ‎ 一、 分类讨论 例3、若时，不等式恒成立，求的取值范围。‎ 解：设，则问题转化为当时，的最小值非负。‎ （1） 当即：时， 又所以不存在；‎ （2） 当即：时， 又 ‎ （3） 当 即：时， 又 综上所得：‎ 二、 确定主元 例4、若不等式对满足的所有都成立，求的取值范围。‎ 解：设，对满足的，恒成立，‎ ‎ 解得：‎ 三、 利用集合与集合间的关系 例5、当时，恒成立，求实数的取值范围。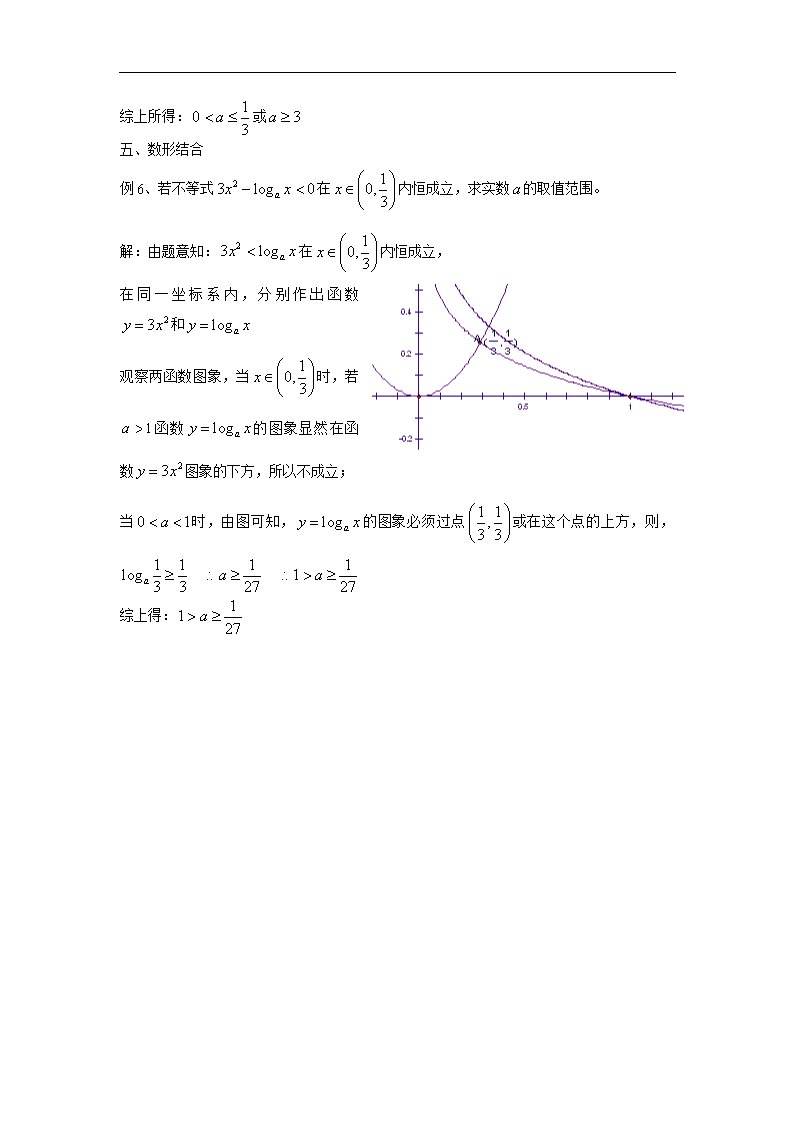‎ 解：‎ （1） 当时，，则问题转化为 ‎ （2） 当时，，则问题转化为 综上所得：或 一、 数形结合 例6、若不等式在内恒成立，求实数的取值范围。‎ 解：由题意知：在内恒成立，‎ 在同一坐标系内，分别作出函数和 观察两函数图象，当时，若函数的图象显然在函数图象的下方，所以不成立；‎ 当时，由图可知，的图象必须过点或在这个点的上方，则， ‎ 综上得：‎