【数学】2014高考专题复习：第9章 解析几何 第1节直线和圆 36页

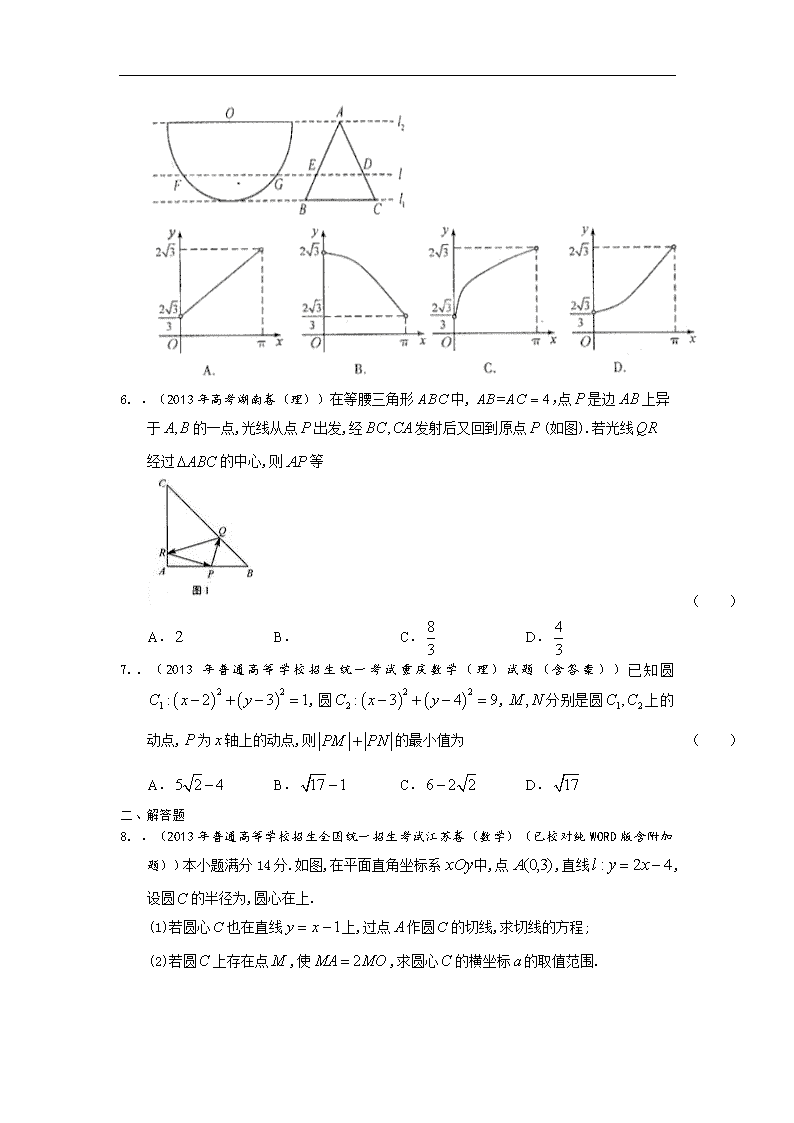
‎【数学】2014版《6年高考4年模拟》‎ 第九章 解析几何 ‎ 第一节直线和圆 第一部分 六年高考荟萃 ‎2013年高考题 一、选择题 ．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD版含答案））已知点,直线将△分割为面积相等的两部分,则的取值范围是 （　　）‎ A． B． ( C) D． ‎ ．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））过点作圆的两条切线,切点分别为,,则直线的方程为 （　　）‎ A． B． C． D．‎ ．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD版））已知点 （　　）‎ A． B． ‎ C． D．‎ ． （2013年高考江西卷（理））过点引直线与曲线相交于A,B两点,O为坐标原点,当AOB的面积取最大值时,直线的斜率等于 （　　）‎ A． B． C． D．‎ ．（2013年高考江西卷（理））如图,半径为1的半圆O与等边三角形ABC夹在两平行线,之间//,与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点,设弧的长为,,若从平行移动到,则函数的图像大致是 ．（2013年高考湖南卷（理））在等腰三角形中,点是边上异于的一点,光线从点出发,经发射后又回到原点(如图).若光线经过的中心,则等 ‎ （　　）‎ A． B． C． D． ‎ ．（2013年普通高等学校招生统一考试重庆数学（理）试题（含答案））已知圆,圆,分别是圆上的动点,为轴上的动点,则的最小值为 （　　）‎ A． B． C． D． ‎ 二、解答题 ．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD版含附加题））本小题满分14分.如图,在平面直角坐标系中,点,直线,设圆的半径为,圆心在上.‎ ‎(1)若圆心也在直线上,过点作圆的切线,求切线的方程;‎ ‎(2)若圆上存在点,使,求圆心的横坐标的取值范围.‎ x y A l O ‎2012年高考题 ．（2012天津理）设,,若直线与圆相切,则的取值范围是（　　）‎ A． B． ‎ C． D．‎ ．（2012浙江理）设aR,则“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的 （　　）‎ A．充分不必要条件 B．必要不充分条件 ‎ C．充分必要条件 D．既不充分也不必要条件 ．（2012重庆理）对任意的实数k,直线y=kx+1与圆的位置关系一定是 （　　）‎ A．相离 B．相切 C．相交但直线不过圆心 D．相交且直线过圆心 ．（2012陕西理）已知圆,过点的直线,则 （　　）‎ A．与相交 B．与相切C．与相离D．以上三个选项均有可能 ．（2012大纲理）正方形的边长为1,点在边上,点在边上,,动点从出发沿直线向运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当点第一次碰到时,与正方形的边碰撞的次数为 （　　）‎ A．16 B．14 C．12 D．10‎ ．（2012年天津理）如图,已知和是圆的两条弦.过点作圆的切线与的延长线相交于点,过点作的平行线与圆相交于点,与相交于点,,,,则线段的长为______________.‎ ．（2012浙江理）定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离.已知曲线C1:y=x 2+a到直线l:y=x的距离等于C2:x 2+(y+4) 2 =2到直线l:y=x的距离,则实数a=______________.‎ ．（2012上海理）若是直线的一个法向量,则的倾斜角的大小为__________(结果用反三角函数值表示).‎ ．（2012山东理）如图,在平面直角坐标系中,一单位圆的圆心的初始位置在,此时圆上一点的位置在,圆在轴上沿正向滚动.当圆滚动到圆心位于时,‎ 的坐标为______________.‎ ．（2012江苏）在平面直角坐标系中,圆的方程为,若直线上至少存在一点,使得以该点为圆心,1为半径的圆与圆有公共点,则的最大值是____.‎ ‎2011年高考题 一、选择题:‎ ‎1．(2011年高考江西卷理科9)若曲线：与曲线：有四个不同的交点，则实数m的取值范围是 ‎ A．(，) B．(，0)∪(0，)‎ ‎ c．[，] D．(，)∪(，+)‎ ‎ ‎ 二、填空题:‎ ‎1.(2011年高考安徽卷理科15)在平面直角坐标系中，如果与都是整数，就称点为整点，下列命题中正确的是_____________（写出所有正确命题的编号）.‎ ‎①存在这样的直线，既不与坐标轴平行又不经过任何整点 ‎②如果与都是无理数，则直线不经过任何整点 ‎③直线经过无穷多个整点，当且仅当经过两个不同的整点 ‎④直线经过无穷多个整点的充分必要条件是：与都是有理数 ‎⑤存在恰经过一个整点的直线 ‎2.(2011年高考重庆卷理科15)设圆位于抛物线与直线所组成的封闭区域（包含边界）内，则圆的半径能取到的最大值为 ‎ 三、解答题:‎ ‎1. (2011年高考山东卷理科22)（本小题满分14分）‎ 已知动直线与椭圆C: 交于P、Q两不同点，且△OPQ的面积=,其中O为坐标原点.‎ ‎（Ⅰ）证明和均为定值;‎ ‎（Ⅱ）设线段PQ的中点为M，求的最大值；‎ ‎（Ⅲ）椭圆C上是否存在点D,E,G，使得?若存在，判断△DEG的形状；若不存在，请说明理由.‎ ‎ ‎ ‎2. (2011年高考广东卷理科19)设圆C与两圆中的一个内切，另一个外切.‎ ‎（1）求C的圆心轨迹L的方程.‎ ‎（2）已知点且P为L上动点，求的最大值及此时点P的坐标.‎ ‎3．(2011年高考福建卷理科17)（本小题满分13分）‎ 已知直线l：y=x+m，m∈R。‎ ‎（I）若以点M（2,0）为圆心的圆与直线l相切与点P，且点P在y轴上，求该圆的方程；‎ ‎（II）若直线l关于x轴对称的直线为，问直线与抛物线C：x2=4y是否相切？说明理由。‎ ‎4．(2011年高考上海卷理科23)（18分）已知平面上的线段及点，在上任取一点，线段长度的最小值称为点到线段的距离，记作。‎ ‎（1）求点到线段的距离；‎ ‎（2）设是长为2的线段，求点集所表示图形的面积；‎ ‎（3）写出到两条线段距离相等的点的集合，其中 ‎，‎ 是下列三组点中的一组。对于下列三组点只需选做一种，满分分别是①2分，②6分，③8分；若选择了多于一种的情形，则按照序号较小的解答计分。‎ ‎① 。‎ ‎② 。‎ ‎③ 。‎ ‎2010年高考题 一、选择题 ‎1.（2010江西理）8.直线与圆相交于M,N两点，若，则k的取值范围是 A. B. C. D. ‎ ‎2.（2010安徽文）（4）过点（1，0）且与直线x-2y-2=0平行的直线方程是 ‎（A）x-2y-1=0 (B)x-2y+1=0 (C)2x+y-2=0 （D）x+2y-1=0‎ ‎3.（2010重庆文）（8）若直线与曲线（）有两个不同的公共点，则实数的取值范围为 ‎（A） （B）‎ ‎（C） （D）‎ ‎4.（2010重庆理）(8) 直线y=与圆心为D的圆交与A、B两点，则直线AD与BD的倾斜角之和为 A. B. C. D. ‎ ‎5.（2010广东文）‎ ‎6.（2010全国卷1理）（11）已知圆O的半径为1，PA、PB为该圆的两条切线，A、B为两切点，那么的最小值为 ‎ (A) (B) (C) (D)‎ ‎7.（2010安徽理）9、动点在圆上绕坐标原点沿逆时针方向匀速旋转，12秒旋转一周。已知时间时，点的坐标是，则当时，动点的纵坐标关于（单位：秒）的函数的单调递增区间是 A、 B、 C、 D、和 二、填空题 ‎1.（2010上海文）7.圆的圆心到直线的距离 。‎ ‎2.（2010湖南文）14.若不同两点P,Q的坐标分别为（a，b），（3-b，3-a），则线段PQ的垂直平分线l的斜率为 ,圆（x-2）2+（y-3）2=1关于直线对称的圆的方程为 ‎ ‎3.（2010全国卷2理）（16）已知球的半径为4，圆与圆为该球的两个小圆，‎ 为圆与圆的公共弦，．若，则两圆圆心的距离 ．‎ O M N E A B ‎4.（2010全国卷2文）（16）已知球的半径为4，圆与圆为该球的两个小圆，为圆与圆的公共弦，，若，则两圆圆心的距离 。‎ ‎5.（2010山东文）（16） 已知圆C过点（1,0），且圆心在x轴的正半轴上，直线l：被该圆所截得的弦长为，则圆C的标准方程为 .‎ ‎6.（2010四川理）（14）直线与圆相交于A、B两点，则 .‎ ‎7.（2010天津文）（14）已知圆C的圆心是直线x-y+1=0与x轴的交点，且圆C与直线x+y+3=0相切。则圆C的方程为 。‎ ‎8.（2010广东理）12.已知圆心在x轴上，半径为的圆O位于y轴左侧，且与直线x+y=0相切，则圆O的方程是 ‎ ‎9.（2010四川文）(14)直线与圆相交于A、B两点，则 .‎ ‎10.（2010山东理）‎ ‎12.（2010江苏卷）9、在平面直角坐标系xOy中，已知圆上有且仅有四个点到直线12x-5y+c=0的距离为1，则实数c的取值范围是___________‎ ‎2009年高考题 一、选择题 ‎1.（辽宁理，4）已知圆C与直线x－y=0 及x－y－4=0都相切，圆心在直线x+y=0上，则圆C的方程为 A. B. ‎ C. D. ‎ ‎2.（重庆理，1）直线与圆的位置关系为（ ）‎ A．相切 B．相交但直线不过圆心 C．直线过圆心 D．相离 ‎3.（重庆文，1）圆心在轴上，半径为1，且过点（1，2）的圆的方程为（ ）‎ A． B． ‎ C． D．‎ ‎4.（上海文，17）点P（4，－2）与圆上任一点连续的中点轨迹方程是　　　（ ）‎ A.　　　　 　B.‎ C.　　　　　　D.‎ ‎5. （上海文，15）已知直线平行，则k得值是（ ） ‎ A. 1或3 B.1或5 C.3或5 D.1或2 ‎ ‎6. (上海文，18)过圆的圆心，作直线分 别交x、y正半轴于点A、B，被圆分成四部分（如图），‎ 若这四部分图形面积满足则直线AB有（ ）‎ ‎（A） 0条 （B） 1条 （C） 2条 （D） 3条 ‎7.（陕西理，4）过原点且倾斜角为的直线被圆学所截得的弦长为科网 A. B.2 C. D.2 ‎ 二、填空题 ‎8. （广东文，13）以点（2，）为圆心且与直线相切的圆的方程是 .‎ ‎9.（天津理，13）设直线的参数方程为（t为参数），直线的方程为y=3x+4则与的距离为_______ ‎ ‎10. （天津文，14）若圆与圆的公共弦长为，则a=________.‎ ‎11.（全国Ⅰ文16）若直线被两平行线所截得的线段的长为，则的倾斜角可以是 ‎ ① ② ③ ④ ⑤ ‎ 其中正确答案的序号是 .（写出所有正确答案的序号）‎ ‎12.（全国Ⅱ理16）已知为圆:的两条相互垂直的弦，垂足为,则四边形的面积的最大值为 。‎ ‎13.（全国Ⅱ文15）已知圆O：和点A（1，2），则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于 ‎ ‎14.（湖北文14）过原点O作圆x2+y2－6x－8y＋20=0的两条切线，设切点分别为P、Q，‎ 则线段PQ的长为 。‎ ‎15.（江西理16）．设直线系,对于下列四个命题：‎ ‎ ．中所有直线均经过一个定点 ‎ ．存在定点不在中的任一条直线上 ‎ ．对于任意整数，存在正边形,其所有边均在中的直线上 ‎ ．中的直线所能围成的正三角形面积都相等 其中真命题的代号是 （写出所有真命题的代号）．‎ 三、解答题 ‎16.（2009江苏卷18）（本小题满分16分） ‎ 在平面直角坐标系中，已知圆和圆.‎ ‎（1）若直线过点，且被圆截得的弦长为，求直线的方程；‎ ‎（2）设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线和，它们分别与圆和圆相交，且直线被圆截得的弦长与直线被圆截得的弦长相等，试求所有满足条件的点P的坐标。‎ ‎2008年高考题 一、选择题 ‎1.（2008年全国Ⅱ理11）等腰三角形两腰所在直线的方程分别为与x-7y-4=0,‎ 原点在等腰三角形的底边上，则底边所在直线的斜率为 （ ）.‎ A．3 B．2 C． D．‎ ‎2.（2008年全国Ⅱ文3）原点到直线的距离为 （ ）‎ A．1 B． C．2 D．‎ ‎3.（2008四川４）将直线绕原点逆时针旋转，再向右平移１个单位长度，所得到的直线为 ( )‎ A.　 　 B.　　‎ C.　 D.‎ ‎4.（2008上海15）如图，在平面直角坐标系中，是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成的区域（含边界），A、B、C、D是该圆的四等分点．若点、点满足且，则称P优于．如果中的点满足：不存在中的其它点优于Q，那么所有这样的点Q组成的集合是劣弧 （　　　）‎ Ａ．　　　　　　　B． C． D．‎ ‎5.（2007重庆文）若直线 与圆相交于P、Q两点，且∠POQ＝120°（其中O为原点），则k的值为 （ ）‎ A.-或 B. C.-或 D.‎ ‎6.（2007天津文）“”是“直线平行于直线”的 （ ）‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 二、填空题 ‎8. （2008天津文15，）已知圆C的圆心与点关于直线y=x+1对称，直线3x+4y-11=0‎ 与圆C相交于两点，且，则圆C的方程为_______. ‎ ‎9.（2008四川文14）已知直线与圆，则 上各点到的距离的最小值为_______.‎ ‎10.（2008广东理11）经过圆的圆心，且与直线垂直的直线 程是 ． ‎ ‎ 第二部分 四年联考汇编 ‎2013-2014年联考题 一．基础题组 ‎1. 【河北省唐山市一中2014届高三12月月考】直线与圆C：交于两点，则的面积为（ ）‎ A． B. C. D. ‎ 二．能力题组 ‎1.【山西省曲沃中学2014届高三上学期期中考试】已知直线a2x＋y＋2＝0与直线bx－(a2＋1)y－1＝0互相垂直，则|ab|的最小值为 (　　)‎ A．5 B．4 C．2 D．1‎ 三、拔高题组 ‎1. 【山西省曲沃中学2014届高三上学期期中考试】已知圆,圆,分别是圆上的动点, 为轴上的动点,则的最小值为（　　）‎ A． B． C． D． ‎ 一．基础题组 ‎1. 【黑龙江省佳木斯市第一中学2013—2014年度高三第三次调研试卷数学试卷（理）】直线和直线平行，则（ ）‎ A． B． C．7或1 D．‎ ‎2. 【黑龙江省佳木斯市第一中学2013—2014年度高三第三次调研试卷数学试卷（理）】已知实数满足，则的最小值是（ ）‎ A． B． C． D．‎ ‎3.【黑龙江省双鸭山一中2014届高三上学期期中考试数学（理）试题】若直线 与的交点在第一象限，则直线的倾斜角的取值范围是（ ）‎ A. B. C. D. ‎ ‎4.【黑龙江省双鸭山一中2014届高三上学期期中考试数学（理）试题】已知直线与互相垂直，则 .‎ 二．能力题组 ‎1.【黑龙江省佳木斯市第一中学2013—2014年度高三第三次调研试卷数学试卷（理）】圆心在曲线上，且与直线相切的面积最小的圆的方程为（ ）‎ A. B.‎ C. D.‎ ‎2.【黑龙江省双鸭山一中2014届高三上学期期中考试数学（理）试题】(本小题满分12分）‎ 已知定点，,直线(为常数). ‎ ‎（1）若点、到直线的距离相等，求实数的值；‎ ‎（2）对于上任意一点，恒为锐角，求实数的取值范围.‎ 三．拔高题组 ‎1. 【黑龙江省佳木斯市第一中学2013—2014年度高三第三次调研试卷数学试卷（理）】（本小题满分12分）‎ 如图，在平面直角坐标系中，点A(0,3),直线：，设圆的半径为1，圆心在上.‎ ‎(1)若圆心也在直线上,过点A作圆的切线,求切线的方程；‎ ‎ (2)若圆上存在点,使,求圆心的横坐标的取值范围.[学科 ‎2.【玉溪一中2013-2014学年上学期期中考试高二数学（理科）试卷】(本小题满分12分)在平面直角坐标系中，已知圆和圆.‎ ‎（1）若直线过点，且被圆截得的弦长为，求直线的方程；‎ ‎ (2）设为平面上的点，满足：存在过点的无穷多对互相垂直的直线和，它们分别与圆和圆相交，且直线被圆截得的弦长与直线被圆截得的弦长相等，试求所有满足条件的点的坐标.‎ ‎ ‎ ‎2012-2013年联考题 ‎1.【天津市新华中学2013届高三第三次月考理】倾斜角为135°，在轴上的截距为的直线方程是（ ）‎ A. B. ‎ C. D. ‎ ‎2.【山东省枣庄三中2013届高三上学期1月阶段测试理】在直角坐标系中，直线的倾斜角是 ‎ A． B． C． D．‎ ‎3.【天津市新华中学2013届高三第三次月考理】若直线：与直线：平行 ，则的值为（ ）‎ A. 1 B. 1或2 C. -2 D. 1或-2 ‎ ‎4.【北京市朝阳区2013届高三上学期期末理】“”是“直线与圆 相交”的 ‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎5.【云南省玉溪一中2013届高三第五次月考理】直线与圆相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最大值为 ( )‎ A. B.2 C. D. ‎ ‎6.【贵州省六校联盟2013届高三第一次联考理】 若点为圆的弦的中点，则弦所在直线方程为（　　）‎ ‎． ． ． ．‎ ‎7.【贵州省遵义四中2013届高三第四次月考理】过点且在轴上的截距和在轴上的截距相等的直线方程为（ ）‎ ‎（A） （B） ‎ ‎（C）或 （D）或 ‎ ‎8.【北京市昌平区2013届高三上学期期末理】以双曲线的右焦点为圆心，并与其渐近线相切的圆的标准方程是 _____.‎ ‎9.【北京市东城区2013届高三上学期期末理】已知圆：，则圆心的坐标为 ；‎ 若直线与圆相切，且切点在第四象限，则 ．‎ ‎10.【北京市丰台区2013届高三上学期期末理】已知直线与平面区域C:的边界交于A，B两点，若，则的取值范围是________.‎ ‎11.【北京市丰台区2013届高三上学期期末理】是分别经过A(1,1)，B(0,-1)两点的两条平行直线，当间的距离最大时，直线的方程是 ．‎ ‎12.【北京市丰台区2013届高三上学期期末理】圆与双曲线的渐近线相切，则的值是 _______. ‎ ‎13.【北京市海淀区2013届高三上学期期末理】点在不等式组 表示的平面区域内，若点到直线的最大距离为，则 ‎14.【北京市石景山区2013届高三上学期期末理】已知不等式组表示的平面区域的面积为，则 ； 若点，则 的最大值为 . ‎ ‎15.【山东省青岛一中2013届高三1月调研理】已知点P的坐标，过点P的直线与圆 相交于A、B两点，则的最小值为 ．‎ ‎2011-2012年联考题 题组一 一、选择题 ‎1．（北京龙门育才学校2011届高三上学期第三次月考）直线x-y+1=0与圆（x+1）2+y2=1的位置关系是 （ ）‎ ‎ A．相切 B．直线过圆心 ‎ ‎ C．直线不过圆心但与圆相交 D．相离 ‎2．（北京五中2011届高三上学期期中考试试题理）若过定点且斜率为的直线与圆在第一象限内的部分有交点，则的取值范围是( ) ‎ ‎ ‎ ‎3、（福建省三明一中2011届高三上学期第三次月考理）两圆和恰有三条公切线，若，且，则的最小值为 （ ）‎ ‎ A． B． C． D．‎ ‎3．（福建省厦门双十中学2011届高三12月月考题理）已知点是曲线C:上的一点，过点与此曲线相切的直线平行于直线，则切线的方程是（ ）‎ A． B．y= [来源:Z&xx&k.Com]‎ C． D．或 ‎4. （福建省厦门双十中学2011届高三12月月考题理）设斜率为1的直线与椭圆相交于不同的两点A、B，则使为整数的直线共有（ ） ‎ A．4条 B．5条 C．6条 D．7条 ‎5.（福建省厦门外国语学校2011届高三11月月考理） 已知圆与抛物线的准线相切，则p＝ （ ▲ ）‎ ‎ A、1 B、2 C、3 D、4‎ ‎6．（甘肃省天水一中2011届高三上学期第三次月考试题理）过点圆的切线,则切线方程为（ ） ‎ A． B．‎ C． D．‎ ‎7．（甘肃省天水一中2011届高三上学期第三次月考试题理）已知圆关于直线 的最小值是（ ）‎ ‎ A．4 B．6 C． 8 D．9‎ ‎8．（广东省惠州三中2011届高三上学期第三次考试理）已知直线与圆交于A、B两点，O是坐标原点，向量、满足 ‎，则实数a的值是（ ）‎ ‎（A）2 （B） （C）或 （D）2或 ‎9. （广东省清远市清城区2011届高三第一次模拟考试理）曲线处的切线方程为（ ）[来源:学|科|网Z|X|X|K]‎ A． B． ‎ C． D．‎ ‎10.（贵州省遵义四中2011届高三第四次月考理）若直线按向量平移后与圆相切，则的值为（    ） ‎ A．8或－2 B．6或－4 C．4或－6 D．2或－8‎ ‎11.（黑龙江大庆实验中学2011届高三上学期期中考试理） 若直线是曲线的切线，则=（ ）‎ ‎ 或 ‎12．（黑龙江哈九中2011届高三12月月考理）“”是“直线”与“直线平行”的 （ ）‎ ‎ A．充分不必要条件 C．必要不充分条件 ‎ ‎ D．充要条件 D．既不充分也不必要条件 ‎13．（湖北省南漳县一中2010年高三第四次月考文）已知α∥β，aα，B∈β，则在β内过点B的所有直线中 ‎ A．不一定存在与a平行的直线 B．只有两条与a平行的直线 ‎ C．存在无数条与a平行的直线 D．存在唯一一条与a平行的直线 ‎14．（重庆市南开中学2011届高三12月月考文）已知圆C与直线都相切，圆心在直线上，则圆C的方程为 （ ）[来源:Z|xx|k.Com]‎ ‎ A． B．‎ ‎ C． D．‎ 二、填空题 ‎14．（湖北省南漳县一中2010年高三第四次月考文）已知两点，则直线与轴的交点分有向线段的比为 　　．‎ ‎15. （福建省厦门外国语学校2011届高三11月月考理）已知椭圆的中心为坐标原点O，焦点在x轴上，斜率为1且过椭圆右焦点的直线交椭圆于A、B两点，共线，求椭圆的离心率__________‎ ‎16．（甘肃省天水一中2011届高三上学期第三次月考试题理）设直线与圆相交于、两点，且弦的长为，则　　　　‎ ‎17. （广东省中山市桂山中学2011届高三第二次模拟考试文） 在极坐标中，圆的圆心到直线的距离为 .‎ ‎18．（河南省郑州市四十七中2011届高三第三次月考文）如下图，直线与圆相切于点，割线经过圆心，弦⊥于点， ，，则 .‎ 第3题 ‎19.（黑龙江省哈尔滨市第162中学2011届高三第三次模拟理）已知函数 的图象关于直线和都对称，且当时，.求 ‎=_____________。‎ ‎20．（湖北省武汉中学2011届高三12月月考）设圆为常数）被轴所截得弦为AB，若弦AB所对圆心角为，则实数 。[来源:学_科_网]‎ 三、简答题 ‎21. （甘肃省天水一中2011届高三上学期第三次月考试题理）（12分）已知圆C经过P（4，– 2），Q（– 1，3）两点，且在y轴上截得的线段长为，半径小于5．‎ ‎（1）求直线PQ与圆C的方程．‎ ‎（2）若直线l∥PQ，且l与圆C交于点A、B，，求直线l的方程．‎ ‎4y=－x2‎ y=－x2‎ ‎22．（福建省四地六校2011届高三上学期第三次联考试题理）‎ ‎（13分）如图，求由两条曲线y=－x2，4y=－x2‎ 及直线y=－1所围成图形的面积.‎ ‎23. （福建省厦门外国语学校2011届高三11月月考理）（本小题满分14分）已知圆O：，点O为坐标原点,一条直线：与圆O相切并与椭圆交于不同的两点A、B ‎ （1）设,求的表达式； ‎ ‎ （2）若，求直线的方程；‎ ‎ （3）若，求三角形OAB面积的取值范围.‎ ‎24．（黑龙江哈九中2011届高三12月月考理）（12分）已知圆及定点，点是圆上的动点，‎ ‎ 点在上，点在上，且满足，．‎ ‎ （1）求的轨迹的方程；‎ ‎ （2） 过点作直线，与曲线交于两点，为坐标原点，设，是否存在这样的直线，使四边形的对角线相等？若存在，求出直线的方程；若不存在，说明理由．‎ ‎25．（黑龙江哈九中2011届高三12月月考理）（12分）已知直线与圆相交于两点，为坐标原点，的面积为．‎ ‎ （1）试将表示成的函数，并求出其定义域；‎ ‎ （2）求的最大值，并求取得最大时的值．‎ 题组二 一、 选择题 ‎1．（广东省河源市龙川一中2011届高三理）‎ 平面内称横坐标为整数的点为“次整点”.过函数图象上任意两个次整点作直线，则倾斜角大于45°的直线条数为（ ）[来源:Z&xx&k.Com]‎ A．10 B．11 C．12 D．13‎ 二、填空题 ‎2．（江苏泰兴市重点中学2011届高三理）函数的图象关于直线对称．则_____________．‎ ‎3．（广东省湛江一中2011届高三10月月考理）‎ 如图，为圆的直径，弦、交于，若，，则 A B C D O P ‎．‎ ‎4．（2011湖南嘉禾一中）（本题满分13 分）‎ ‎ 已知椭圆的右焦点F 与抛物线y2 = 4x 的焦点重合，短轴长为2．椭圆的右准线l与x轴交于E，过右焦点F 的直线与椭圆相交于A、B 两点，点C 在右准线l 上，BC//x 轴．‎ ‎ （1）求椭圆的标准方程，并指出其离心率；‎ ‎ （2）求证：线段EF被直线AC 平分．‎ ‎5．（江苏泰兴2011届高三理）（本小题满分14分）‎ ‎ 已知：在函数的图象上，以为切点的切线的倾斜角为 ‎ （I）求的值；‎ ‎ （II）是否存在最小的正整数，使得不等式恒成立？如果存在，请求出最小的正整数，如果不存在，请说明理由。‎ ‎6．（福建省福州八中2011届高三文）（本小题满分14分）‎ 已知椭圆经过点（0，1），离心率 ‎（I）求椭圆C的方程；‎ ‎（II）设直线与椭圆C交于A，B两点，点A关于x轴的对称点为A’.试问：当m变化时直线与x轴是否交于一个定点？若是，请写出定点坐标，并证明你的结论；若不是，请说明理由。‎ ‎7. （河北省唐山一中2011届高三理）已知过点（1,1）且斜率为（）的直线与轴分别交于两点，分别过作直线的垂线，垂足分别为求四边形的面积的最小值.‎ ‎8. （福建省四地六校联考2011届高三理）（本小题满分14分）本题（1）、（2）、（3）三个选答题，每小题7分，任选2题作答，满分14分，如果多做，则按所做的前两题计分。作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中。‎ ‎（1）(本小题满分7分) 选修4-2:矩阵与变换 已知，若所对应的变换把直线变换为自身，求实数，并求的逆矩阵。‎ ‎（2）（本题满分7分）选修4-4：坐标系与参数方程 ‎ 已知直线的参数方程：（为参数）和圆的极坐标方程：。‎ ①将直线的参数方程化为普通方程，圆的极坐标方程化为直角坐标方程；‎ ②判断直线和圆的位置关系。‎ ‎（3）（本题满分7分）选修4-5：不等式选讲 ‎ 已知函数 ①解不等式；‎ ②证明：对任意，不等式成立.‎ ‎2010年联考题 ‎1.（马鞍山学业水平测试）如果方程表示焦点在轴上的椭圆,那么实数的取值范围是 A. (0,+∞) B. (0,2) C. (1,+∞) 　D. (0,1)‎ ‎2.（池州市七校元旦调研）已知直线y=x+1与曲线相切，则α的值为( ) ‎ ‎(A)1 (B)2 (C) -1 (D)-2‎ ‎3.曲线在点处的切线方程为 （ ） ‎ ‎ A. B. C. D. ‎ ‎4.（昆明一中三次月考理）是圆上任意一点，若不等式恒成立，则c的取值范围是 ‎ A． B．‎ ‎ C． D．‎ ‎5.（岳野两校联考）若直线和圆O：没有交点，则过点的直线与椭圆的交点个数为（ ）‎ A．至多一个 B．2个 C．1个 D．0个 ‎6．（昆明一中四次月考理）已知直线与圆交于A、B两点，O是坐标原点，向量、满足，则实数a的值是（ ）‎ ‎（A）2 （B） （C）或 （D）2或 ‎7．（哈师大附中、东北师大附中、辽宁省实验中学）圆的方程为，圆的方程为，过圆上任意一点作圆的两条切线、，切点分别为、，则的最小值是 （ ）‎ A．12 B．10 C．6 D．5‎ ‎8.（马鞍山学业水平测试）如果过两点和的直线与抛物线没有交点，那么实数的取值范围是　　　　　　　　　　.　 ‎ ‎9．（安庆市四校元旦联考）已知点M（－3，0），N（3，0），B（1，0），圆C与直线MN切于点B，过M、N与圆C相切的两直线相交于点P，则P点的轨迹方程为 .‎ ‎10. （安庆市四校元旦联考）设直线的方程为，将直线绕原点 按逆时针方向旋转得到直线，则的方程是 。‎ ‎11．（安庆市四校元旦联考）（本题满分16分）如图，在矩形中，，以为圆心1为半径的圆与交于（圆弧为圆在矩形内的部分）‎ ‎（Ⅰ）在圆弧上确定点的位置，使过的切线平分矩形ABCD的面积；‎ ‎（Ⅱ）若动圆与满足题（Ⅰ）的切线及边都相切，试确定的位置，使圆为矩形内部面积最大的圆．‎