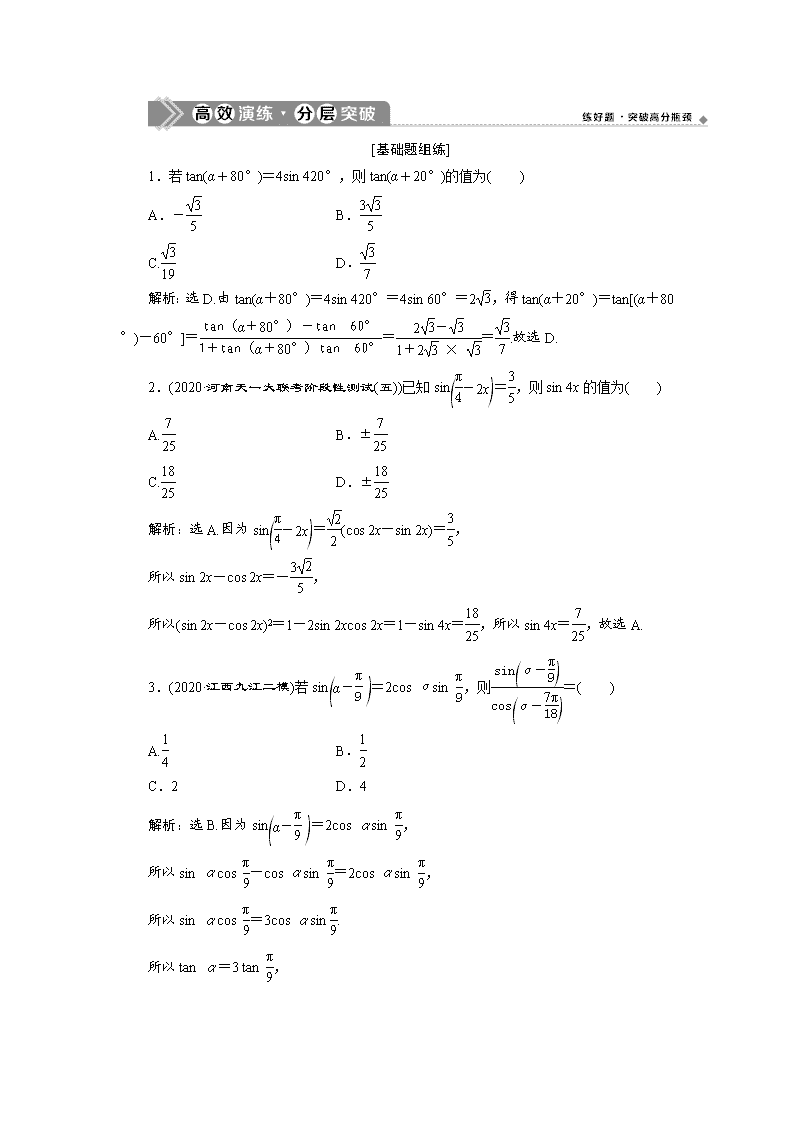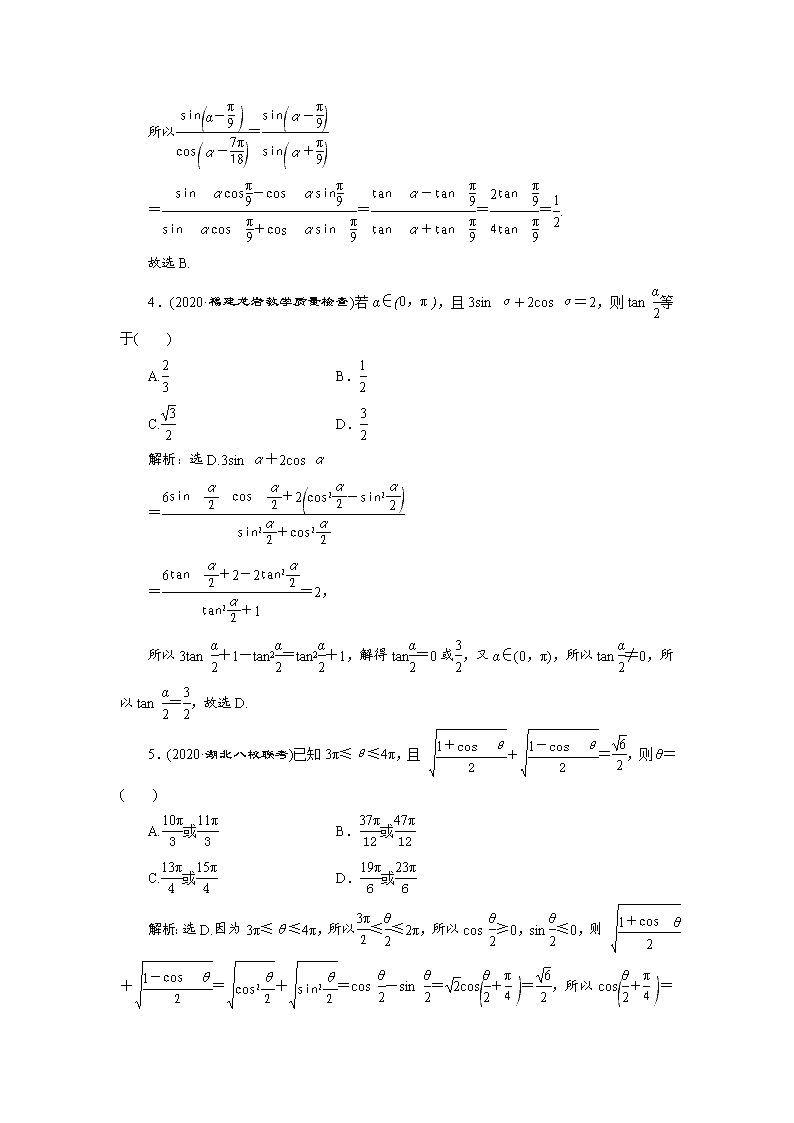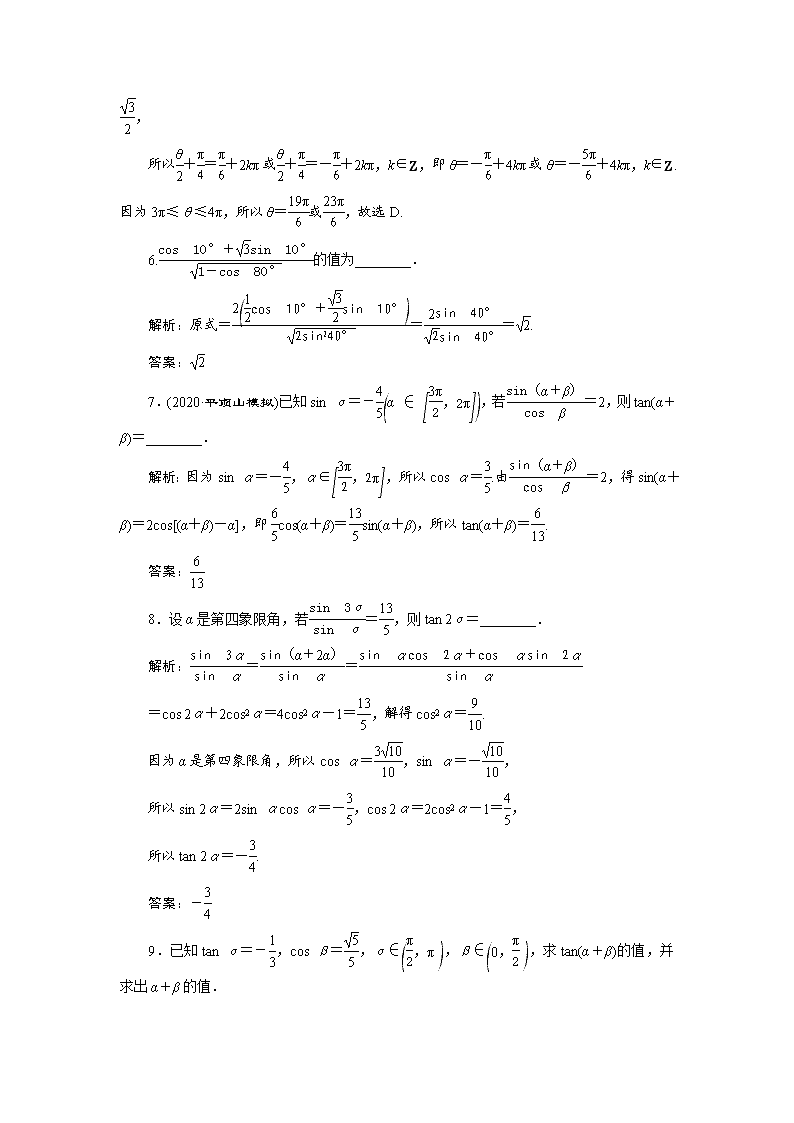2021届北师大版高考理科数一轮复习高效演练分层突破：第四章　第3讲　第2课时　简单的三角恒等变形 8页

‎[基础题组练]‎ ‎1．若tan(α＋80°)＝4sin 420°，则tan(α＋20°)的值为(　　)‎ A．－　　　　　　　　 B． C. D． 解析：选D.由tan(α＋80°)＝4sin 420°＝4sin 60°＝2，得tan(α＋20°)＝tan[(α＋80°)－60°]＝＝＝.故选D.‎ ‎2．(2020·河南天一大联考阶段性测试(五))已知sin＝，则sin 4x的值为(　　)‎ A. B．± C. D．± 解析：选A.因为sin＝(cos 2x－sin 2x)＝，‎ 所以sin 2x－cos 2x＝－，‎ 所以(sin 2x－cos 2x)2＝1－2sin 2xcos 2x＝1－sin 4x＝，所以sin 4x＝，故选A.‎ ‎3．(2020·江西九江二模)若sin＝2cos αsin ，则＝(　　)‎ A. B． C．2 D．4‎ 解析：选B.因为sin＝2cos αsin ，‎ 所以sin αcos －cos αsin ＝2cos αsin ，‎ 所以sin αcos ＝3cos αsin .‎ 所以tan α＝3 tan ，‎ 所以＝ ‎＝＝＝＝.‎ 故选B.‎ ‎4．(2020·福建龙岩教学质量检查)若α∈，且3sin α＋2cos α＝2，则tan 等于(　　)‎ A. B． C. D． 解析：选D.3sin α＋2cos α ‎＝ ‎＝＝2，‎ 所以3tan ＋1－tan2＝tan2＋1，解得tan＝0或，又α∈(0，π)，所以tan ≠0，所以tan ＝，故选D.‎ ‎5．(2020·湖北八校联考)已知3π≤θ≤4π，且 ＋＝，则θ＝(　　)‎ A.或　　　　　　 B．或 C.或 D．或 解析：选D.因为3π≤θ≤4π，所以≤≤2π，所以cos ≥0，sin ≤0，则 ＋＝＋＝cos －sin ＝cos＝，所以cos＝，‎ 所以＋＝＋2kπ或＋＝－＋2kπ，k∈Z，即θ＝－＋4kπ或θ＝－＋4kπ，k∈Z.因为3π≤θ≤4π，所以θ＝或，故选D.‎ ‎6.的值为________．‎ 解析：原式＝＝＝.‎ 答案： ‎7．(2020·平顶山模拟)已知sin α＝－，若＝2，则tan(α＋β)＝________．‎ 解析：因为sin α＝－，α∈，所以cos α＝.由＝2，得sin(α＋β)＝2cos[(α＋β)－α]，即cos(α＋β)＝sin(α＋β)，所以tan(α＋β)＝.‎ 答案： ‎8．设α是第四象限角，若＝，则tan 2α＝________．‎ 解析：＝＝ ‎＝cos 2α＋2cos2α＝4cos2α－1＝，解得cos2α＝.‎ 因为α是第四象限角，所以cos α＝，sin α＝－，‎ 所以sin 2α＝2sin αcos α＝－，cos 2α＝2cos2α－1＝，‎ 所以tan 2α＝－.‎ 答案：－ ‎9．已知tan α＝－，cos β＝，α∈，β∈，求tan(α＋β)的值，并求出α＋β的值．‎ 解：由cos β＝，β∈，‎ 得sin β＝，tan β＝2.‎ 所以tan(α＋β)＝ ‎＝＝1.‎ 因为α∈，β∈，‎ 所以<α＋β<，‎ 所以α＋β＝.‎ ‎10．已知函数f(x)＝4tan x·sin·cos－.‎ ‎(1)求f(x)的定义域与最小正周期；‎ ‎(2)讨论f(x)在区间上的单调性．‎ 解：(1)f(x)的定义域为.‎ f(x)＝4tan xcos xcos－ ‎＝4sin xcos－ ‎＝4sin x－ ‎＝2sin xcos x＋2sin2x－ ‎＝sin 2x＋(1－cos 2x)－ ‎＝sin 2x－cos 2x＝2sin.‎ 所以f(x)的最小正周期T＝＝π.‎ ‎(2)因为x∈，‎ 所以2x－∈，‎ 由y＝sin x的图象可知，当2x－∈，‎ 即x∈时，f(x)递减；当2x－∈，即x∈时，f(x)递增．‎ 所以当x∈时，f(x)在区间上递增，在区间上递减．‎ ‎[综合题组练]‎ ‎1．设α∈，β∈，且tan α＝，则下列结论中正确的是(　　)‎ A．α－β＝ B．α＋β＝ C．2α－β＝ D．2α＋β＝ 解析：选A.tan α＝＝＝＝＝tan.因为α∈，β＋∈，所以α＝β＋，即α－β＝.‎ ‎2．若sin 2α＝，sin(β－α)＝，且α∈，β∈，则α＋β的值是(　　)‎ A. B． C.或 D．或 解析：选A.因为α∈，β∈，‎ 所以2α∈.‎ 又0