高中数学第8章圆锥曲线方程（第9课时）双曲线及其标准方程(2) 6页

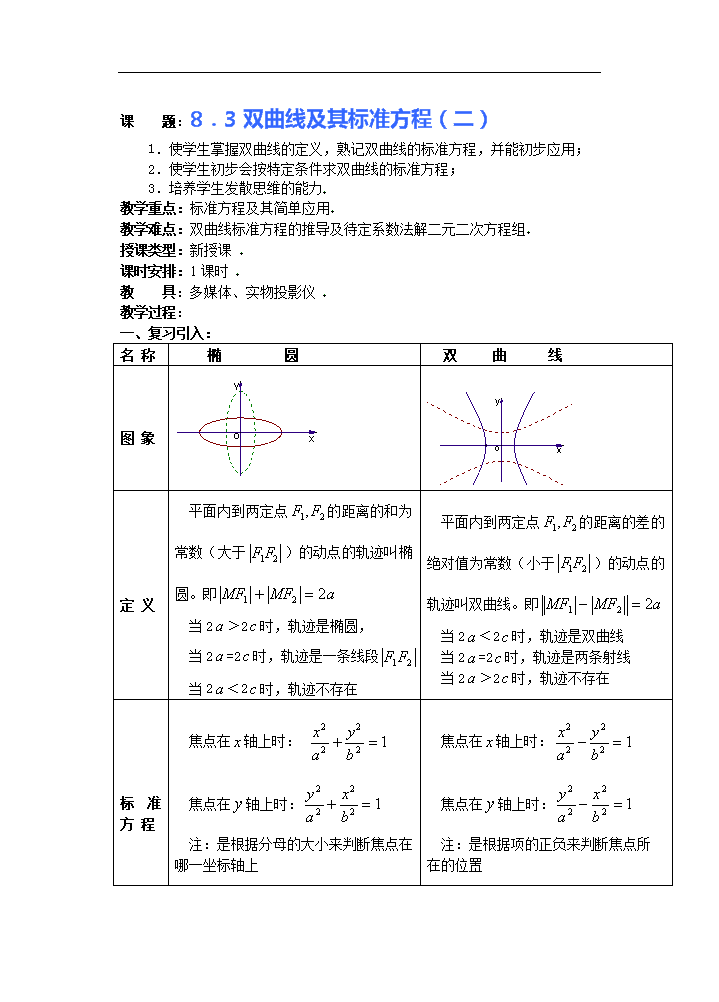
课 题：8．3双曲线及其标准方程（二）‎ ‎1．使学生掌握双曲线的定义，熟记双曲线的标准方程，并能初步应用；‎ ‎2．使学生初步会按特定条件求双曲线的标准方程； ‎ ‎3．培养学生发散思维的能力 教学重点：标准方程及其简单应用 教学难点：双曲线标准方程的推导及待定系数法解二元二次方程组 授课类型：新授课 ‎ 课时安排：1课时 ‎ 教 具：多媒体、实物投影仪 ‎ 教学过程：‎ 一、复习引入： ‎ 名 称 椭 圆 双 曲 线 图 象 定 义 ‎ 平面内到两定点的距离的和为常数（大于）的动点的轨迹叫椭圆。即 ‎ 当2﹥2时，轨迹是椭圆，‎ ‎ 当2=2时，轨迹是一条线段 ‎ 当2﹤2时，轨迹不存在 平面内到两定点的距离的差的绝对值为常数（小于）的动点的轨迹叫双曲线。即 当2﹤2时，轨迹是双曲线 当2=2时，轨迹是两条射线 当2﹥2时，轨迹不存在 标准方 程 ‎ ‎ 焦点在轴上时： ‎ 焦点在轴上时： ‎ 注：是根据分母的大小来判断焦点在哪一坐标轴上 焦点在轴上时： ‎ 焦点在轴上时：‎ 注：是根据项的正负来判断焦点所 在的位置 常数的关 系 ‎ ‎ （符合勾股定理的结构）‎ ‎，‎ ‎ 最大，‎ ‎（符合勾股定理的结构）‎ 最大，可以 二、讲解范例：‎ 例1 已知双曲线的焦点在轴上，中心在原点，且点，，在此双曲线上，求双曲线的标准方程 分析：由于已知焦点在轴上，中心在原点，所以双曲线的标准方程可用设出来，进行求解 本题是用待定系数法来解的，得到的关于待定系数的一个分式方程组，并且分母的次数是2，解这种方程组时利用换元法可将它化为二元二次方程组；也可将的倒数作为未知数，直接看作二元一次方程组 ‎ 解：因为双曲线的焦点在轴上，中心在原点，所以设所求双曲线的标准方程为 ‎ ‎ （）‎ 则有 ，即 解关于的二元一次方程组，得 ‎ 所以，所求双曲线的标准方程为 ‎ 变式例题1 点A位于双曲线上，是它的两个焦点，求的重心G的轨迹方程 ‎ 分析：要求重心的轨迹方程，必须知道三角形的三个顶点的坐标，利用相关点法进行求解 注意限制条件 ‎ 解：设的重心G的坐标为，则点A的坐标为 因为点A位于双曲线上，从而有 ‎，即 所以，的重心G的轨迹方程为 ‎ 点评：求轨迹方程，常用的方法是直接求法和间接求法两种 例1是直接利用待定系数法求轨迹方程 本题则是用间接法(也叫代入法)来解题，补充本例是为了进一步提高学生分析问题和解决问题的能力 另外本题所求轨迹中包含一个隐含条件，它表现为轨迹上点的坐标应满足一个不等关系，而这一点正是学生容易忽略，造成错误的地方，所以讲解本题有利于培养学生数学思维的缜密性，养成严谨细致的学习品质 ‎ 变式例题2 已知的底边BC长为12，且底边固定，顶点A是动点，使，求点A的轨迹 分析：首先建立坐标系，由于点A的运动规律不易用坐标表示，注意条件的运用，可利用正弦定理将其化为边的关系，注意有关限制条件 解：以底边BC 为轴，底边BC的中点为原点建立坐标系，这时 ‎，由得 ‎,即 ‎ 所以，点A的轨迹是以为焦点，2=6的双曲线的左支 其方程为：‎ 点评 ‎：求轨迹方程的过程中，有一个重要的步骤就是找出(或联想到)轨迹上的动点所满足的几何条件，列方程就是根据这些条件确定的，由于轨迹问题比较普遍，题型多样，有些轨迹上的动点满足的几何条件可能比较隐蔽和复杂解决它需要突出形数结合的思考方法，运用逻辑推理，结合平面几何的基本知识，分析、归纳，这里安排本例就是针对以上情况来进行训练的 ‎ 例2　 一炮弹在某处爆炸，在A处听到爆炸声的时间比在B处晚2s．‎ ‎(1)爆炸点应在什么样的曲线上？‎ ‎(2)已知A、B两地相距800m，并且此时声速为340 m／s，求曲线的方程．‎ 分析：解应用题的关键是建立数学模型 根据本题设和结论，注意到在A处听到爆炸声的时间比B处晚2s,这里声速取同一个值 ‎ 解：(1)由声速及A、B两处听到爆炸声的时间差，可知A、B两处与爆炸点的距离的差，因此爆炸点应位于以A、B为焦点的双曲线上 因为爆炸点离A处比离B处更远，所以爆炸点应在靠近B处的一支上．‎ ‎(2)如图，建立直角坐标系，使A、B两点在轴上，并且点O与线段AB的中点重合 设爆炸点P的坐标为，则 |PA|－|PB|=340×2=680，即 2＝680，＝340．‎ 又|AB|=800， ∴　 2c=800，c=400，＝44400‎ ‎∵　 |PA|－|PB|＝680＞0，‎ ‎∴　 ＞0‎ 所求双曲线的方程为 ‎ （＞0）‎ 例2说明，利用两个不同的观测点测得同一炮弹爆炸声的时间差，可以确定爆炸点所在的双曲线的方程，但不能确定爆炸点的准确位置．如果再增设一个观测点C，利用B、C(或A、C)两处测得的爆炸声的时间差，可以求出另一个双曲线的方程，解这两个方程组成的方程组，就能确定爆炸点的准确位置．这是双曲线的一个重要应用 想一想，如果A、B两处同时听到爆炸声，那么爆炸点应在什么样的曲线上．（爆炸点应在线段AB的中垂线上）‎ 点评：本例是培养学生应用双曲线知识解决实际问题的一道典型题目，安排在此非常有利于强化学生“应用数学”的意识，后面对“想一想”的教学处理，有利于调动学生的学习主动性和积极性，培养他们的发散思维能力 例3求与圆及都外切的动圆圆心的轨迹方程 解：设动圆的半径为r，则由动圆与定圆都外切得 ‎，‎ 又因为，‎ 由双曲线的定义可知，点M的轨迹是双曲线的一支 所求动圆圆心的轨迹是双曲线的一支，其方程为： ‎ 三、课堂练习：‎ ‎1．判断方程所表示的曲线。‎ 解：①当时，即当时，是椭圆；‎ ‎②当时，即当时，是双曲线；‎ ‎2．求焦点的坐标是（-6，0）、（6，0），并且经过点A（-5，2）的双曲线的标准方程。‎ 答案： ‎ ‎3．求经过点和，焦点在y轴上的双曲线的标准方程答案：‎ ‎4．椭圆和双曲线有相同的焦点，则实数的值是 （ ）‎ ‎ A B C 5 D 9‎ 答案：B ‎5．已知是双曲线的焦点，PQ是过焦点的弦，且PQ的倾斜角为600，那么的值为（答案： 4＝16）‎ ‎6．设是双曲线的焦点，点P在双曲线上,且,则点P到轴的距离为( )‎ ‎ A 1 B C 2 D ‎ 答案：B 的面积为，从而有 ‎ ‎7．P为双曲线上一点，若F是一个焦点，以PF为直径的圆与圆的位置关系是（）‎ A 内切 B 外切 C 外切或内切 D 无公共点或相交 答案：C ‎ 四、小结 ：本课着重讲解了待定系数法，代入法及利用定义求双曲线的标准方程，学习了双曲线的一个重要应用 ‎ 五、课后作业：‎ 六、板书设计（略）‎ 七、课后记： ‎