2013年全国高校自主招生数学模拟试卷6 7页

‎2013年全国高校自主招生数学模拟试卷六 一、选择题(36分)‎ ‎1．删去正整数数列1，2，3，……中的所有完全平方数，得到一个新数列．这个数列的第2003项是 ‎ (A) 2046 (B) 2047 (C) 2048 (D) 2049‎ ‎2．设a，b∈R，ab≠0，那么直线ax－y+b=0和曲线bx2+ay2=ab的图形是 ‎ ‎ ‎3．过抛物线y2=8(x+2)的焦点F作倾斜角为60°的直线，若此直线与抛物线交于A、B两点，弦AB的中垂线与x轴交于点P，则线段PF的长等于 ‎(A) (B) (C) (D) 8 ‎4．若x∈[－，－]，则y=tan(x+)－tan(x+)+cos(x+)的最大值是 ‎ (A) (B) (C) (D) ‎5．已知x，y都在区间(－2，2)内，且xy=－1，则函数u=+的最小值是 ‎(A) (B) (C) (D) ‎6．在四面体ABCD中， 设AB=1，CD=，直线AB与CD的距离为2，夹角为，则四面体ABCD的体积等于 ‎ (A) (B) (C) (D) 二．填空题(每小题9分，共54分)‎ ‎7．不等式|x|3－2x2－4|x|+3<0的解集是 ．‎ ‎8．设F1、F2是椭圆+=1的两个焦点，P是椭圆上一点，且|PF1|∶|PF2|=2∶1，则△PF‎1F2的面积等于 ．‎ ‎9．已知A={x|x2－4x+3<0，x∈R}，‎ B={x|21－x+a≤0，x2－2(a+7)x+5≤0，x∈R}‎ 若AÍB，则实数a的取值范围是 ．‎ ‎10．已知a，b，c，d均为正整数，且logab=，logcd=，若a－c=9，则b－d= ．‎ ‎11．将八个半径都为1的球分放两层放置在一个圆柱内，并使得每个球都和其相邻的四个球相切，且与圆柱的一个底面及侧面都相切，则此圆柱的高等于 ．‎ ‎12． 设Mn={(十进制)n位纯小数0.|ai只取0或1(i=1，2，…，n－1)，an=1}，Tn 是Mn中元素的个数，Sn是Mn中所有元素的和，则= ．‎ 三、（20分）‎ ‎13．设≤x≤5，证明不等式 ‎ 2++<2．‎ 四、(20分)‎ ‎14．设A、B、C分别是复数Z0=ai，Z1=+bi，Z2=1+ci(其中a，b，c都是实数)对应的不共线的三点．证明：曲线 ‎ Z=Z0cos4t+2Z1cos2tsin2t+Z2sin4t (t∈R)‎ 与△ABC中平行于AC的中位线只有一个公共点，并求出此点．‎ 五、(本题满分20分)‎ ‎ 15．一张纸上画有一个半径为R的圆O和圆内一个定点A，且OA=a，折叠纸片，使圆周上某一点A¢刚好与点A重合．这样的每一种折法，都留下一条折痕．当A¢取遍圆周上所有点时，求所有折痕所在直线上点的集合．‎ ‎2013年全国高校自主招生数学模拟试卷六 参考答案 一、选择题(每小题6分，共36分)‎ ‎1．删去正整数数列1，2，3，……中的所有完全平方数，得到一个新数列．这个数列的第2003项是 ‎ (A) 2046 (B) 2047 (C) 2048 (D) 2049‎ 解：452=2025，462=2116．‎ 在1至2025之间有完全平方数45个，而2026至2115之间没有完全平方数．故1至2025中共有新数列中的2025－45=1980项．还缺2003－1980=23项．由2025+23=2048．知选C．‎ ‎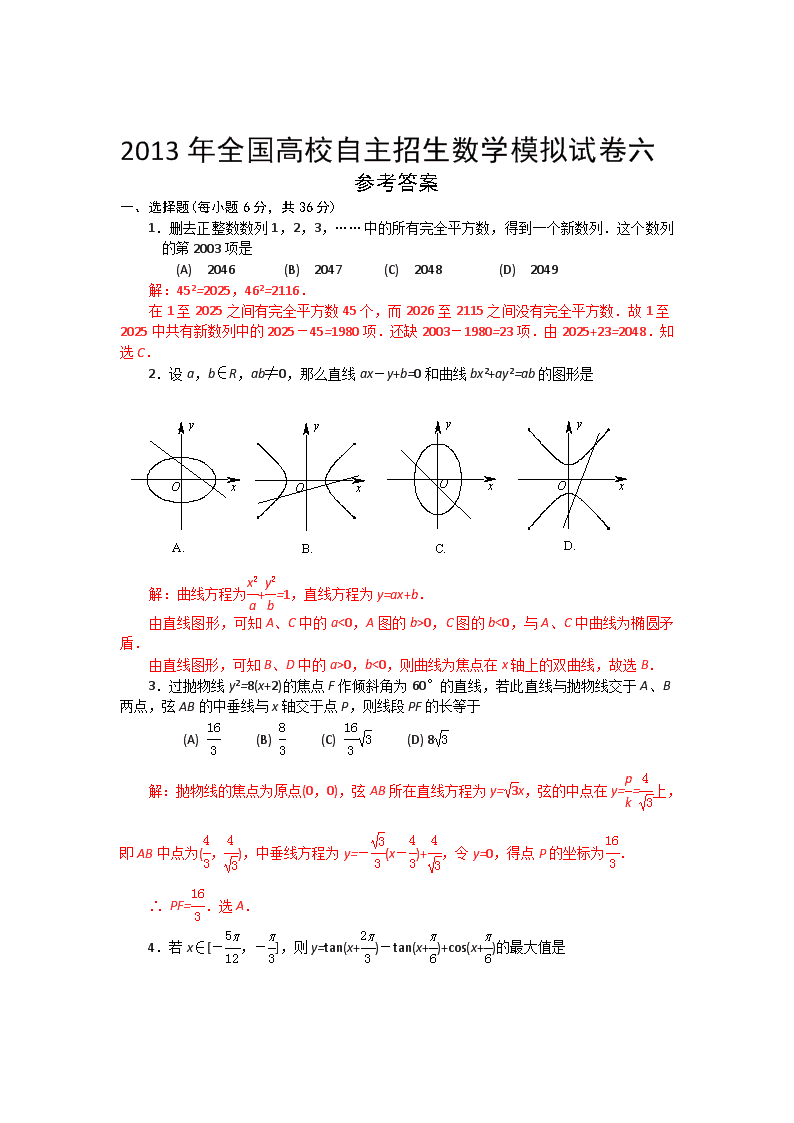2．设a，b∈R，ab≠0，那么直线ax－y+b=0和曲线bx2+ay2=ab的图形是 ‎ ‎ 解：曲线方程为+=1，直线方程为y=ax+b．‎ 由直线图形，可知A、C中的a<0，A图的b>0，C图的b<0，与A、C中曲线为椭圆矛盾．‎ 由直线图形，可知B、D中的a>0，b<0，则曲线为焦点在x轴上的双曲线，故选B． ‎ ‎3．过抛物线y2=8(x+2)的焦点F作倾斜角为60°的直线，若此直线与抛物线交于A、B两点，弦AB的中垂线与x轴交于点P，则线段PF的长等于 ‎ (A) (B) (C) (D) 8 解：抛物线的焦点为原点(0，0)，弦AB所在直线方程为y=x，弦的中点在y==上，即AB中点为(，)，中垂线方程为y=－(x－)+，令y=0，得点P的坐标为．‎ ‎∴ PF=．选A．‎ ‎4．若x∈[－，－]，则y=tan(x+)－tan(x+)+cos(x+)的最大值是 ‎ (A) (B) (C) (D) 解：令x+=u，则x+=u+，当x∈[－，－]时，u∈[－，－]，‎ y=－(cotu+tanu)+cosu=－+cosu．在u∈[－，－]时，sin2u与cosu都单调递增，从而y单调递增．于是u=－时，y取得最大值，故选C．‎ ‎5．已知x，y都在区间(－2，2)内，且xy=－1，则函数u=+的最小值是 ‎(A) (B) (C) (D) 解：由x，y∈(－2，2)，xy=－1知，x∈(－2，－)∪(，2)，‎ u=+==1+．‎ 当x∈(－2，－)∪(，2)时，x2∈(，4)，此时，9x2+≥12．(当且仅当x2=时等号成立)．‎ 此时函数的最小值为，故选D．‎ ‎6．在四面体ABCD中， 设AB=1，CD=，直线AB与CD的距离为2，夹角为，则四面体ABCD的体积等于 ‎ (A) (B) (C) (D) 解：如图，把四面体补成平行六面体，则此平行六面体的体积=1××sin×2=3．‎ 而四面体ABCD的体积=×平行六面体体积=．故选B．‎ 二．填空题(每小题9分，共54分)‎ ‎7．不等式|x|3－2x2－4|x|+3<0的解集是 ．‎ 解：即|x|3－2|x|2－4|x|+3<0，Þ(|x|－3)(|x|－)(|x|+)<0．Þ|x|<－，或<|x|<3．‎ ‎∴ 解为(－3，－)∪(，3)．‎ ‎8．设F1、F2是椭圆+=1的两个焦点，P是椭圆上一点，且|PF1|∶|PF2|=2∶1，则△PF‎1F2的面积等于 ．‎ 解：F1(－，0)，F2(，0)；|F‎1F2|=2．‎ ‎ |PF1|+|PF2|=6，Þ|PF1|=4，|PF2|=2．由于42+22=(2)2．故DPF‎1F2是直角三角形 ‎．‎ ‎∴ S=4．‎ ‎9．已知A={x|x2－4x+3<0，x∈R}，‎ B={x|21－x+a≤0，x2－2(a+7)x+5≤0，x∈R}‎ 若AÍB，则实数a的取值范围是 ．‎ 解：A=(1，3)；‎ 又，a≤－21－x∈(－1，－)，当x∈(1，3)时，a≥ －7∈(－7，－4)．‎ ‎∴ －4≤a≤－1．‎ ‎10．已知a，b，c，d均为正整数，且logab=，logcd=，若a－c=9，则b－d= ‎ 解：a3=b2，c5=d4，设a=x2，b=x3；c=y4，d=y5，x2－y4=9．(x+y2)(x－y2)=9．‎ ‎∴ x+y2=9，x－y2=1，x=5，y2=4．b－d=53－25=125－32=93．‎ ‎11．将八个半径都为1的球分放两层放置在一个圆柱内，并使得每个球都和其相邻的四个球相切，且与圆柱的一个底面及侧面都相切，则此圆柱的高等于 ．‎ 解：如图，ABCD是下层四个球的球心，EFGH是上层的四个球心．每个球心与其相切的球的球心距离=2．EFGH在平面ABCD上的射影是一个正方形．是把正方形ABCD绕其中心旋转45°而得．设E的射影为N，则 MN=－1．EM=，故EN2=3－(－1)2=2．∴ EN=．所求圆柱的高=2+．‎ ‎12． 设Mn={(十进制)n位纯小数0.|ai只取0或1(i=1，2，…，n－1)，an=1}，Tn 是Mn中元素的个数，Sn是Mn中所有元素的和，则= ．‎ 解：由于a1，a2，…，an－1中的每一个都可以取0与1两个数，Tn=2n－1．‎ 在每一位(从第一位到第n－1位)小数上，数字0与1各出现2n－2次．第n位则1出现2n－1次．‎ ‎∴ Sn=2n－2´0.11…1+2n－2´10－n．‎ ‎∴ =´=．‎ 三、（本题满分20分）‎ ‎13．设≤x≤5，证明不等式 ‎ 2++<2．‎ ‎ 解：x+1≥0，2x－3≥0，15－3x≥0．Þ≤x≤5．‎ 由平均不等式≤≤．‎ ‎∴ 2++=+++≤2．‎ ‎ 但2在≤x≤5时单调增．即2≤2=2．‎ ‎ 故证．‎ 四、(本题满分20分)‎ ‎14．设A、B、C分别是复数Z0=ai，Z1=+bi，Z2=1+ci(其中a，b，c都是实数)对应的不共线的三点．证明：曲线 ‎ Z=Z0cos4t+2Z1cos2tsin2t+Z2sin4t (t∈R)‎ 与△ABC中平行于AC的中位线只有一个公共点，并求出此点．‎ 解：曲线方程为：Z=aicos4t+(1+2bi)cos2tsin2t+(1+ci)sin4t=(cos2tsin2t+sin4t)+i(acos4t+2bcos2tsin2t+csin4t)‎ ‎∴ x=cos2tsin2t+sin4t=sin2t(cos2t+sin2t)=sin2t．(0≤x≤1)‎ ‎ y=acos4t+2bcos2tsin2t+csin4t=a(1－x)2+2b(1－x)x+cx2‎ ‎ 即 y=(a－2b+c)x2+2(b－a)x+a (0≤x≤1)． ①‎ ‎ 若a－2b+c=0，则Z0、Z1、Z2三点共线，与已知矛盾，故a－2b+c¹0．于是此曲线为轴与x轴垂直的抛物线．‎ AB中点M：+(a+b)i，BC中点N：+(b+c)i．‎ 与AC平行的中位线经过M(，(a+b))及N(，(b+c))两点，其方程为 ‎4(a－c)x+4y－‎3a－2b+c=0．(≤x≤)． ②‎ 令 4(a－2b+c)x2+8(b－a)x+‎4a=4(c－a)x+‎3a+2b－c．‎ 即4(a－2b+c)x2+4(2b－a－c)x+a－2b+c=0．由a－2b+c¹0，得 ‎4x2+4x+1=0，‎ 此方程在[，]内有惟一解： x=．‎ 以x=代入②得， y=(a+2b+c)．‎ ‎∴ 所求公共点坐标为(，(a+2b+c))．‎ 五、(本题满分20分)‎ ‎15．一张纸上画有一个半径为R的圆O和圆内一个定点A，且OA=a，折叠纸片，使圆周上某一点A¢刚好与点A重合．这样的每一种折法，都留下一条折痕．当A¢取遍圆周上所有点时，求所有折痕所在直线上点的集合．‎ 解：对于⊙O上任意一点A¢，连AA¢，作AA¢的垂直平分线MN，连OA¢．交MN于点P．显然OP+PA=OA¢=R．由于点A在⊙O内，故OA=aa)为长轴的椭圆C．‎ 而MN上任一异于P的点Q，都有OQ+QA=OQ+QA¢>OA¢．故点Q在椭圆C外．即折痕上所有的点都在椭圆C上及C外．‎ 反之，对于椭圆C上或外的一点S，以S为圆心，SA为半径作圆，交⊙O于A¢，则S在AA¢的垂直平分线上，从而S在某条折痕上．‎ 最后证明所作⊙S与⊙O必相交．‎ ‎1° 当S在⊙O外时，由于A在⊙O内，故⊙S与⊙O必相交；‎ ‎2° 当S在⊙O内时(例如在⊙O内，但在椭圆C外或其上的点S¢)，取过S¢的半径OD，则由点S¢在椭圆C外，故OS¢+S¢A≥R(椭圆的长轴)．即S¢A≥S¢D．于是D在⊙S¢内或上，即⊙S¢与⊙O必有交点．‎ 于是上述证明成立．‎ 综上可知，折痕上的点的集合为椭圆C上及C外的所有点的集合．‎ ‎ ‎