高考文科数学复习备课课件：第六节　双曲线 30页

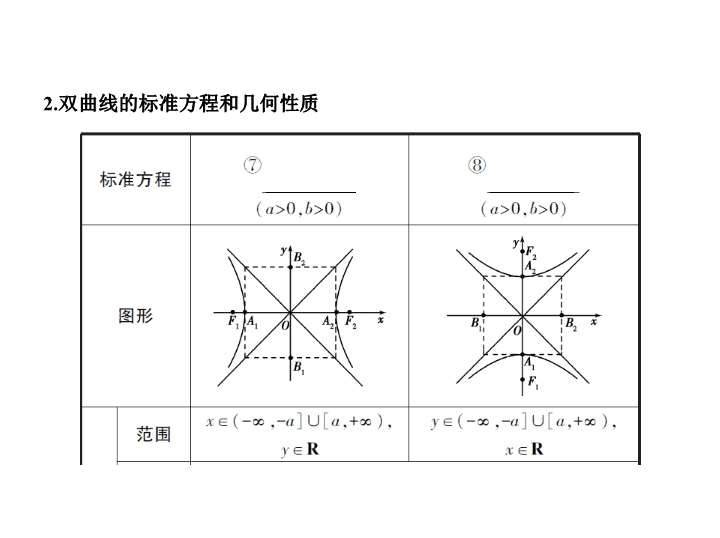
文数 课标版 第六节　双曲线 1.双曲线的定义 平面内与两个定点 F 1 、 F 2 的① 　距离的差的绝对值     等于常数(小于| F 1 F 2 |且不等于零)的点的轨迹叫做双曲线.这两个定点叫做 ② 　双曲线的焦点     ,两焦点间的距离叫做③ 　双曲线的焦距     . 集合 P ={ M ||| MF 1 |-| MF 2 ||=2 a },| F 1 F 2 |=2 c ,其中 a 、 c 为常数且 a >0, c >0. 教材研读 (1)当④ 　2 a <| F 1 F 2 |     时, P 点的轨迹是双曲线; (2)当⑤ 　2 a =| F 1 F 2 |     时, P 点的轨迹是两条射线; (3)当⑥ 　2 a >| F 1 F 2 |     时, P 点不存在. 2.双曲线的标准方程和几何性质   判断下列结论的正误(正确的打“√”,错误的打“ × ”) (1)平面内到点 F 1 (0,4), F 2 (0,-4)距离之差等于8的点的轨迹是双曲线.   ( × ) (2)平面内到点 F 1 (0,4), F 2 (0,-4)距离之差的绝对值等于6的点的轨迹是双 曲线.   (√) (3)方程   -   =1( mn >0)表示焦点在 x 轴上的双曲线.   ( × ) (4)等轴双曲线的渐近线互相垂直,离心率等于   .   (√) (5)双曲线方程   -   = λ ( m >0, n >0, λ ≠ 0)的渐近线方程是   -   =0,即   ±   =0.   (√) 1.双曲线2 x 2 - y 2 =8的实轴长是   (　　) A.2　    B.2   　    C.4　    D.4   答案     C　双曲线2 x 2 - y 2 =8的标准方程为   -   =1,故实轴长为4. 2.双曲线方程为 x 2 -2 y 2 =1,则它的右焦点坐标为   (　　) A.   　    B.   　    C.   　    D.(   ,0) 答案     C　∵原方程可化为   -   =1, ∴ a 2 =1, b 2 =   ,∴ c 2 = a 2 + b 2 =   ,∴右焦点坐标为   . 3.若双曲线 E :   -   =1的左、右焦点分别为 F 1 、 F 2 ,点 P 在双曲线 E 上,且 | PF 1 |=3,则| PF 2 |等于   (　　) A.11　    B.9　    C.5　    D.3 答案     B　| PF 1 |=3< a + c =8,故点 P 在双曲线的左支上,由双曲线的定义得 | PF 2 |-| PF 1 |=2 a =6,所以| PF 2 |=9,故选B. 4.“ ab <0”是“方程   +   =1表示焦点在 x 轴上的双曲线”的   (　　) A.充分而不必要条件　    B.必要而不充分条件 C.充分必要条件　    D.既不充分也不必要条件 答案     B　当 ab <0时,有 a <0, b >0和 a >0, b <0两种情况.①当 a <0, b >0时,方 程   +   =1表示焦点在 y 轴上的双曲线;②当 a >0, b <0时,方程   +   =1表 示焦点在 x 轴上的双曲线.因此,当 ab <0时,方程   +   =1不一定表示焦点 在 x 轴上的双曲线.而方程   +   =1表示焦点在 x 轴上的双曲线时,有 a >0, b <0,则 ab <0.由此可得,“ ab <0”是“方程   +   =1表示焦点在 x 轴上的 双曲线”的必要而不充分条件.故选B. 5.若点 P (2,0)到双曲线   -   =1( a >0, b >0)的一条渐近线的距离为   ,则 双曲线的离心率为   (　　) A.   　    B.   　    C.2   　    D.2   答案     A　双曲线的渐近线方程为 bx ± ay =0,点 P (2,0)到渐近线的距离为   =   ,所以 a 2 = b 2 ,所以 c 2 =2 a 2 ,所以双曲线的离心率为   ,故选A. 6.设中心在原点的双曲线与椭圆   + y 2 =1有公共的焦点,且它们的离心 率互为倒数,则该双曲线的方程是 　　　　　　     . 答案 　2 x 2 -2 y 2 =1 解析　 ∵椭圆的焦点为( ± 1,0),∴双曲线的焦点为( ± 1,0).∵椭圆的离心 率 e =   ,∴双曲线的离心率 e '=   . ∴双曲线中 c 2 =2 a 2 ,∴1=2 a 2 ,∴ a 2 =   , 又双曲线中 b 2 = c 2 - a 2 ,∴ b 2 =   , ∴所求双曲线的方程为2 x 2 -2 y 2 =1. 考点一　双曲线的定义及标准方程 典例1 　(1)已知 F 1 、 F 2 为双曲线 C : x 2 - y 2 =2的左、右焦点,点 P 在 C 上,| PF 1 | =2| PF 2 |,则cos∠ F 1 PF 2 =   (　　) A.   　    B.   　    C.   　    D.   (2)已知双曲线   -   =1( a >0, b >0)和椭圆   +   =1有相同的焦点,且双曲 线的离心率是椭圆离心率的两倍,则双曲线的方程为 　　　　　　          . 答案 　(1)C　(2)   -   =1 解析 　(1)双曲线方程可化为   -   =1,∴ a = b =   ,∴ c =2.由 考点突破   得| PF 1 |=4   ,| PF 2 |=2   ,由余弦定理得cos∠ F 1 PF 2 =   =   .故选C. (2)由题易得椭圆焦点为( ±   ,0),离心率为   , ∴在双曲线中有 a 2 + b 2 =7且 e =   =   , 结合 a 2 + b 2 = c 2 解得 a 2 =4, b 2 =3, ∴双曲线的方程为   -   =1. 方法技巧 (1) 在双曲线的定义中要注意双曲线上的点 ( 动点 ) 具备的几何条件 , 即 “到两定点 ( 焦点 ) 的距离之差的绝对值为一个常数 , 且该常数必须小于 两定点间的距离”.若去掉定义中的“绝对值”,则点的轨迹是双曲线 的一支.同时注意定义的转化应用. (2)求双曲线方程时,一是注意标准形式的判断;二是注意 a 、 b 、 c 的关 系. 变式1-1 　若将本例(1)中的条件“| PF 1 |=2| PF 2 |”改为“∠ F 1 PF 2 =60 ° ”, 则△ F 1 PF 2 的面积是多少? 解析　 不妨设点 P 在双曲线的右支上,则| PF 1 |-| PF 2 |=2 a =2   , 在△ F 1 PF 2 中,由余弦定理,得 cos∠ F 1 PF 2 =   =   , 所以| PF 1 |·| PF 2 |=8, 所以   =   | PF 1 |·| PF 2 |sin 60 ° =2   . 1-2　 过双曲线 C :   -   =1的右顶点作 x 轴的垂线,与 C 的一条渐近线相 交于点 A .若以 C 的右焦点为圆心、4为半径的圆经过 A , O 两点( O 为坐标 原点),则双曲线 C 的方程为   (　　) A.   -   =1　    B.   -   =1 C.   -   =1　    D.   -   =1 答案     A　由双曲线方程知右顶点为( a ,0),不妨设其中一条渐近线方程 为 y =   x ,因此可设点 A 的坐标为( a , b ).设右焦点为 F ( c ,0),由已知可知 c =4, 且| AF |=4,即( c - a ) 2 + b 2 =16,所以有( c - a ) 2 + b 2 = c 2 ,得 a 2 -2 ac + b 2 =0,又知 c 2 = a 2 + b 2 , 所以得 a 2 -2 ac + c 2 - a 2 =0,即 a =   =2,所以 b 2 = c 2 - a 2 =4 2 -2 2 =12.故双曲线的方程 为   -   =1,故选A. 考点二　双曲线的几何性质 命题角度一　双曲线的离心率问题 典例2     (2016山东,14,5分)已知双曲线 E :   -   =1( a >0, b >0).矩形 ABCD 的四个顶点在 E 上, AB , CD 的中点为 E 的两个焦点,且2| AB |=3| BC |,则 E 的 离心率是 　　　     . 答案 　2 解析 　由已知得| AB |=| CD |=   ,| BC |=| AD |=| F 1 F 2 |=2 c .因为2| AB |=3| BC |,所 以   =6 c ,2 b 2 =3 ac ,   =3 e ,2( e 2 -1)=3 e ,2 e 2 -3 e -2=0,解得 e =2,或 e =-   (舍去). 典例3 　(1)已知双曲线的渐近线方程为 y = ±   x ,且经过点 A (2,-3),则双曲 线的标准方程为   (　　) A.   -   =1　    B.   -   =1 C.   -   =1　    D.   -   =1 (2)过双曲线   -   =1( a >0, b >0)的左焦点 F 作圆 O : x 2 + y 2 = a 2 的两条切线,切 点为 A , B ,双曲线左顶点为 C ,若∠ ACB =120 ° ,则双曲线的渐近线方程为   (　　) A. y = ±   x 　    B. y = ±   x C. y = ±   x 　    D. y = ±   x 命题角度二　双曲线的渐近线问题 答案 　(1)B　(2)A 解析 　(1)由题意设双曲线的方程为 x 2 -4 y 2 = λ ( λ ≠ 0). 因为点 A (2,-3)在双曲线上,所以4-4 × (-3) 2 = λ , 解得 λ =-32,故双曲线的方程为   -   =1. (2)如图所示, C (- a ,0),连接 OA , OB ,设双曲线   -   =1( a >0, b >0)的焦距为 2 c ( c >0),则 F (- c ,0).   由双曲线和圆的对称性知,点 A 与点 B 关于 x 轴对称,则∠ ACO =∠ BCO =   ∠ ACB =   × 120 ° =60 ° . 因为| OA |=| OC |= a ,所以△ ACO 为等边三角形, 所以∠ AOC =60 ° . 因为 FA 与圆 O 切于点 A ,所以 OA ⊥ FA , 在Rt△ AOF 中,∠ AFO =90 ° -∠ AOF =90 ° -60 ° =30 ° , 所以| OF |=2| OA |,即 c =2 a , 所以 b =   =   =   a , 故双曲线   -   =1( a >0, b >0)的渐近线方程为 y = ±   x = ±   x . 典例4 　(1)中心在原点,焦点在 x 轴上的双曲线的一条渐近线经过点 (4,-2),则它的离心率为   (　　) A.   　    B.   　    C.   　    D.   (2)过双曲线 C :   -   =1( a >0, b >0)的右焦点作一条与其渐近线平行的直 线,交 C 于点 P .若点 P 的横坐标为2 a ,则 C 的离心率为 　　　     . 答案 　(1)D　(2)2+   解析 　(1)设双曲线的标准方程为   -   =1( a >0, b >0), 所以其渐近线方程为 y = ±   x ,因为点(4,-2)在渐近线上, 所以   =   ,根据 c 2 = a 2 + b 2 ,可得   =   , e 2 =   ,即 e =   . 命题角度三　离心率与渐近线的综合问题 (2)如图所示,不妨令与渐近线平行的直线的斜率为   ,又直线过右焦点 ( c ,0),则直线的方程为 y =   ( x - c ).   把点 P 的横坐标2 a 代入双曲线方程得   -   =1,解得 y =-   b 或 y =   b (点 P 在 x 轴下方,故舍去),故点 P 的坐标为(2 a ,-   b ),代入直线方程得-   b =   (2 a - c ),化简可得离心率 e =   =2+   . 典例5     (2015课标全国Ⅰ,5,5分)已知 M ( x 0 , y 0 )是双曲线 C :   - y 2 =1上的一 点, F 1 , F 2 是 C 的两个焦点.若   ·   <0,则 y 0 的取值范围是   (　　) A.   　    B.   C.   　    D.   答案     A 解析 　若   ·   =0,则点 M 在以原点为圆心,半焦距 c =   为半径的圆 上,则   解得   =   .可知:   ·   <0 ⇒ 点 M 在圆 x 2 + y 2 =3的内部 ⇒   <   ⇒ y 0 ∈   .故选A. 命题角度四　求参数或变量的取值范围 规律总结 (1)求双曲线离心率或离心率范围的方法:一种是直接建立 e 的关系式求 e 或 e 的范围;另一种是建立 a , b , c 的齐次关系式,将 b 用 a , c 表示,令两边同 除以 a 或 a 2 化为 e 的关系式,进而求解. (2)方程   -   =1与   -   =1,当 a 1 + b 1 = a 2 + b 2 时焦距相等,当   =   时渐近 线相同. (3)双曲线   -   =1的渐近线方程为   -   =0. 2-1　 已知 F 是双曲线 C :   -   =1( a >0, b >0)的右焦点, O 是双曲线 C 的中 心,直线 y =   x 是双曲线 C 的一条渐近线,以线段 OF 为边作正三角形 AOF ,若点 A 在双曲线 C 上,则 m 的值为   (　　) A.3+2   　    B.3-2   　    C.3+   　    D.3-   答案     A　由题意知   =   , m =   , A   在双曲线上,故   -   =1, 得 m =3+2   (舍负),故选A. 2-2　 已知 P 是双曲线   -   =1右支上任意一点, M 是圆( x +5) 2 + y 2 =1上任 意一点,设 P 到双曲线的渐近线的距离为 d ,则 d +| PM |的最小值为 　　          . 答案　 9 解析 　设双曲线的左、右焦点分别为 F 1 , F 2 ,根据题意可得 d +| PM | ≥ d + | PF 1 |-1= d +6+| PF 2 |-1= d +| PF 2 |+5,结合图象(图略)可知 d +| PF 2 |的最小值为 F 2 到渐近线的距离,因为 F 2 到渐近线的距离为4,所以 d +| PM |的最小值为9. 考点三　直线与双曲线的位置关系 典例6 　已知中心在原点的双曲线 C 的右焦点为(2,0),右顶点为(   ,0). (1)求该双曲线 C 的方程; (2)若直线 l : y = kx +   与双曲线 C 左支有两个不同的交点 A , B ,求 k 的取值范 围. 解析　 (1)由题意设双曲线方程为   -   =1( a >0, b >0).由已知得 a =   , c = 2,再由 a 2 + b 2 = c 2 ,得 b 2 =1.故双曲线 C 的方程为   - y 2 =1. (2)设 A ( x A , y A ), B ( x B , y B ), 将 y = kx +   代入   - y 2 =1, 得(1-3 k 2 ) x 2 -6   kx -9=0. 由题意知   解得   < k <1. ∴ k 的取值范围为   < k <1. 方法技巧 (1)研究直线与双曲线位置关系问题的方法:将直线方程代入双曲线方 程,消元,得关于 x 或 y 的方程,当二次项系数等于0时,直线与双曲线相交 于某支上一点;当二次项系数不等于0时,用判别式 Δ 来判定. (2)用“点差法”可以解决弦中点和弦斜率的有关问题. 3-1 　已知双曲线 E 的中心为原点, F (3,0)是 E 的焦点,过 F 的直线 l 与 E 相交 于 A , B 两点,且 AB 的中点为 N (-12,-15),则 E 的方程为 　　　　　　     . 答案        -   =1 解析 　设双曲线 E 的方程为   -   =1( a >0, b >0), 由题意知 c =3,则 a 2 + b 2 =9. 设 A ( x 1 , y 1 ), B ( x 2 , y 2 ), 则有   得   =   =   =   ,