高中数学必修1教案：第四章（第32课时）已知三角函数值求角（2） 7页

课 题：411已知三角函数值求角（2）‎ 教学目的：‎ ‎1．要求学生初步（了解）理解反正切函数的意义，会由已知角的正弦值、余弦、正切值求出范围内的角，并能用反正弦，反余弦，反正切的符号表示角或角的集合 ‎2．掌握已知三角函数值求角的解题步骤．‎ 教学重点：已知三角函数值求角 教学难点：诱导公式与利用三角函数值求角的综合运用 授课类型：新授课 课时安排：1课时 教 具：多媒体、实物投影仪 教学过程：‎ 一、复习引入：‎ ‎1．反正弦，反余弦函数的意义：‎ x y ‎0‎ 由 ‎1°在R上无反函数 ‎2°在上， x与y是一一对应的，且区间比较简单 在上，的反函数称作反正弦函数，‎ 记作，（奇函数）‎ x y ‎0‎ 同理，由 在上，的反函数称作反余弦函数，‎ 记作 ‎2．已知三角函数求角：‎ 求角的多值性法则：1、先决定角的象限2、如果函数值是正值，则先求出对应的锐角x； 如果函数值是负值，则先求出与其绝对值对应的锐角x，3、由诱导公式，求出符合条件的其它象限的角 x ‎0‎ y 二、讲解新课： ‎ 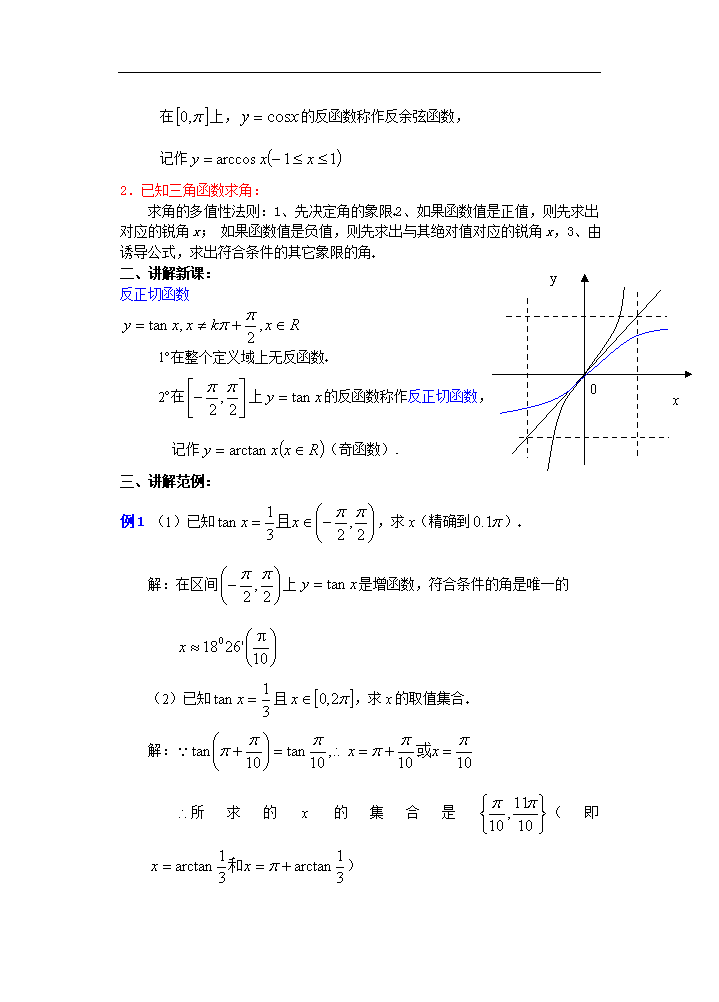反正切函数 ‎ 1°在整个定义域上无反函数 ‎ 2°在上的反函数称作反正切函数，‎ ‎ 记作（奇函数）‎ 三、讲解范例：‎ 例1 （1）已知，求x（精确到）‎ 解：在区间上是增函数，符合条件的角是唯一的 ‎ ‎ ‎（2）已知且，求x的取值集合 解：‎ ‎ 所求的x的集合是（即）‎ ‎（3）已知，求x的取值集合 解：由上题可知：，‎ 合并为 ‎ 例2已知，根据所给范围求：‎ ‎ 1°为锐角 2°为某三角形内角 3°为第二象限角 4° ‎ 解：1°由题设 ‎ 2°设，或 ‎ 3° ‎ 4°由题设 ‎ 例3 求适合下列关系的x的集合 ‎ 1° 2° 3° ‎ 解：1° ‎ 所求集合为 ‎ 2°所求集合为 ‎ 3° ‎ 例4 直角锐角A，B满足：‎ ‎ 解：由已知：‎ ‎ 为锐角，‎ ‎ ‎ 例5 1°用反三角函数表示中的角x ‎2°用反三角函数表示中的角x 解：1° ∵ ∴‎ ‎ 又由 得 ‎ ∴ ∴‎ ‎ 2° ∵ ∴‎ ‎ 又由 得 ‎ ∴ ∴‎ 例6已知，求角x的集合 解：∵ ∴‎ ‎ 由 得 ‎ ‎ 由 得 ‎ ‎ 故角x的集合为 例7求的值 解：arctan2 = a, arctan3 = b 则tana = 2， tanb = 3‎ ‎ 且， ‎ ‎ ∴‎ ‎ 而 ∴a + b = ‎ ‎ 又arctan1 = ∴= p 例8求y = arccos(sinx), ()的值域 解：设u = sin x ∵ ∴‎ ‎ ∴ ∴所求函数的值域为 四、课堂练习：‎ ‎1若cosx＝0，则角x等于( )‎ A．ｋπ，（ｋ∈Z） Ｂ．＋ｋπ，（ｋ∈Z）‎ Ｃ．＋2ｋπ，（ｋ∈Z） Ｄ．－＋2ｋπ，（ｋ∈Z）‎ ‎2若tanx＝0，则角x等于( )‎ A．ｋπ，（ｋ∈Z） Ｂ．＋ｋπ，（ｋ∈Z）‎ Ｃ．＋2ｋπ，（ｋ∈Z） Ｄ．－＋2ｋπ，（ｋ∈Z）‎ ‎3已知cosx＝－，π＜x＜2π，则x等于( )‎ A． Ｂ． Ｃ． Ｄ．‎ ‎4若tan（3π－x）＝－，则x= ‎ ‎5满足tanx＝的x的集合为 ‎ ‎6在闭区间［0，2π］上，适合关系式cosx＝－0．4099的角有 个,用0．4099的反余弦表示的x值是 ___________；用－04099的反余弦表示的x的值是 _________‎ 参考答案：‎ ‎1B 2A 3A 4x＝＋kπ，k∈Z 5｛x｜x＝arctaｎ＋kπ，k∈Z｝‎ ‎6两 π－arccos04099 π＋arccos04099 ‎ arccos(－04099) 2π－arccos(－04099)‎ 五、小结：反正切函数的有关概念，并能运用知识已知三角函数值求角 ‎ 六、课后作业：‎ ‎1方程cosx＝a（｜a｜＜1，x∈［0，2π的解的集合是( )‎ A．｛arccosa，－arccosa｝ Ｂ．｛arccosa｝‎ Ｃ．｛arccosa，π－arccosa｝ Ｄ．｛arccosa，2π－arccosa｝‎ ‎2适合cosx＝－，x∈（－π，－）的x值是( )‎ A． arccos（－） Ｂ．π－arccos Ｃ．－arccos（－） Ｄ．－arccos ‎3若tanα＝8，且α∈（，），则α等于( )‎ A．arctan8 Ｂ．arctan8－π Ｃ．π－arctan8 Ｄ．π＋arctan8‎ ‎4已知3tan2x＝1，x是第三象限角，则x的集合是 ‎ ‎5若tanθ＝88，且tan83°31′＝88，则θ的集合为 ‎ ‎6若cos2x＝－且0＜x＜2π，则x等于 ‎ ‎7求满足sinxcosx－sinx－cosx－1＝0的x ‎8已知sinx＋cosx＝1，求．‎ ‎9求满足cos（πsinx）＝的x的集合 参考答案：‎ ‎1D 2C 3D 4x＝＋2kπ，k∈Z ‎5｛θ｜θ＝83°31′＋k·180°，k∈Z｝‎ ‎6 ‎ ‎7x＝－＋2kπ或x＝π＋2kπ，k∈Z ‎81 9｛x｜x＝±arcsin＋kπ，k∈Z｝‎ 七、板书设计（略）‎ 八、课后记：‎ ‎ ‎