高考文科数学复习备课课件：第一节　坐标系 28页

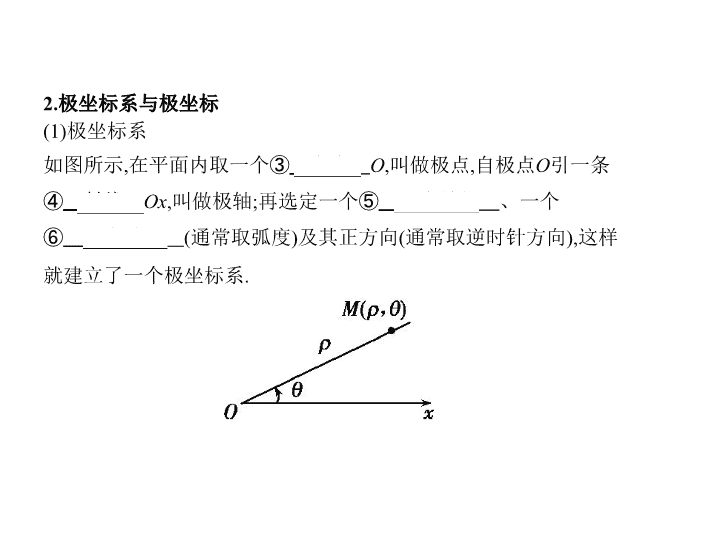
文数 课标 版 第一节　坐标系 1.平面直角坐标系中的坐标伸缩变换 设点 P ( x , y )是平面直角坐标系中的任意一点,在变换 φ :   的作用下,点 P ( x , y )对应到点 P '( x ', y '),称 φ 为平面直角 坐标系中的坐标伸缩变换,简称伸缩变换. 教材研读 2.极坐标系与极坐标 (1)极坐标系 如图所示,在平面内取一个③ 　定点     O ,叫做极点,自极点 O 引一条 ④     射线     Ox ,叫做极轴;再选定一个⑤ 　长度单位     、一个 ⑥ 　角度单位     (通常取弧度)及其正方向(通常取逆时针方向),这样 就建立了一个极坐标系. (2)极坐标 (i)极径:设 M 是平面内一点,极点 O 与点 M 的⑦ 　距离     | OM |叫做点 M 的 极径,记为 ρ . (ii)极角:以极轴 Ox 为始边,射线 OM 为终边的角 xOM 叫做点 M 的极角,记 为 θ . (iii)极坐标:有序数对( ρ , θ )叫做点 M 的极坐标,记为 M ( ρ , θ ). 3.极坐标与直角坐标的互化 设 M 是平面内任意一点,它的直角坐标是( x , y ),极坐标是( ρ , θ ),则它们之间 的关系为       1.曲线 y =sin x 经过变换   后得到曲线 C ,则曲线 C 的周期 T 和 y max 分 别为   (　　) A. T =π, y max =3　    B. T =4π, y max =3 C. T =π, y max =   　    D. T =4π, y max =   答案     A　由   得   将其代入 y =sin x 得   y '=sin 2 x ', 即 y '=3sin 2 x '. 即曲线 C 的解析式为 y =3sin 2 x , 故 T =   =π, y max =3,故选A. 2.椭圆 C : x 2 +9 y 2 =9经过变换 Γ 后变成圆 x 2 + y 2 =1.则变换 Γ 为   (　　) A.   　    B.   C.   　    D.   答案     B　设变换 Γ :   则   将其代入 x 2 +9 y 2 =9得   +9·   =9, 即   x ' 2 +   y ' 2 =1. 由题意得   ∴   故选B. 3.在极坐标系中, A   , B   两点间的距离为   (　　) A.2　    B.3　    C.6　    D.3   答案     C　解法一:(数形结合)在极坐标系中, A , B 两点如图所示,| AB |=| OA |+| OB |=6.   解法二: A   , B   的直角坐标为 A   ,即 A (1,- ), B   ,即 B (-2,2   ). ∴| AB |=   =   =6.故选C. 4.在极坐标系中,圆心为(   ,π)且过极点的圆的方程为 　　　　　　     . 答案      ρ =-2   cos θ 解析 　如图, O 为极点, C 为圆心, OB 为直径,设 A ( ρ , θ ), 则∠ ABO = θ -90 ° , OB =2   =   , 化简得 ρ =-2   cos θ .   5.(2015北京,11,5分)在极坐标系中,点   到直线 ρ (cos θ +   sin θ )=6的 距离为 　　　     . 答案 　1 解析 　由极坐标与直角坐标的互化公式可得,点   对应的直角坐标 为(1,   ),直线 ρ (cos θ +   sin θ )=6对应的直角坐标方程为 x +   y =6,由点 到直线的距离公式可得,所求距离为   =1. 考点一　平面直角坐标系中的伸缩变换 典例1 　在同一平面直角坐标系中,经过伸缩变换   后,曲线 C 1 : x 2 + y 2 =36变为曲线 C 2 . (1)求 C 2 的方程; (2) P 、 Q 分别为 C 1 与 C 2 上的点,求| PQ |的最小值与最大值. 解析 　(1)设圆 x 2 + y 2 =36上任一点为 A ( x , y ),伸缩变换后对应的点的坐标 为 A '( x ', y '), 则   ∴4 x ' 2 +9 y ' 2 =36, 考点突破 即   +   =1. ∴曲线 C 2 的方程为   +   =1. (2) C 1 是以 O 为圆心,半径 r =6的圆, C 2 是以 O 为中心,长半轴长 a =3,短半轴 长 b =2的椭圆(如图). ∴| PQ | min = r - a =6-3=3. | PQ | max = r + a =6+3=9.   方法技巧 平面上的曲线 y = f ( x )在变换 φ :   的作用下的变换方程的求法 是将   代入 y = f ( x ),将   = f   整理之后得到 y '= h ( x '),即为所求变换 之后的方程. 1-1 　在同一平面直角坐标系中,将直线 x -2 y =2变成直线2 x '- y '=4,则满足 图象变换的伸缩变换为   (　　) A.   　    B.   C.   　    D.   答案     D　设伸缩变换为   又2 x '- y '=4,所以2 λx - μy =4, 即 λx -   y =2, 又 x -2 y =2,故 λ =1, μ =4, 所以伸缩变换为   1-2 　双曲线 C : x 2 -   =1经过 φ :   变换后所得曲线 C '的焦点坐标为 　　　　　     . 答案 　(-5,0),(5,0) 解析 　设曲线 C '上任意一点为 P '( x ', y '),由题意可知,将   代入 x 2 -   =1,得   -   =1,化简得   -   =1,即   -   =1为曲线 C '的方程,其焦点 坐标为(-5,0),(5,0). 考点二　极坐标方程与直角坐标方程的互化 典例2     (2015课标Ⅰ,23,10分)在直角坐标系 xOy 中,直线 C 1 : x =-2,圆 C 2 :( x - 1) 2 +( y -2) 2 =1,以坐标原点为极点, x 轴的正半轴为极轴建立极坐标系. (1)求 C 1 , C 2 的极坐标方程; (2)若直线 C 3 的极坐标方程为 θ =   ( ρ ∈R),设 C 2 与 C 3 的交点为 M , N ,求 △ C 2 MN 的面积. 解析 　(1)因为 x = ρ cos θ , y = ρ sin θ ,所以 C 1 的极坐标方程为 ρ cos θ =-2, C 2 的 极坐标方程为 ρ 2 -2 ρ cos θ -4 ρ sin θ +4=0. (2)解法一:将 θ =   代入 ρ 2 -2 ρ cos θ -4 ρ sin θ +4=0,得 ρ 2 -3   ρ +4=0,解得 ρ 1 = 2   , ρ 2 =   ,故 ρ 1 - ρ 2 =   ,即| MN |=   . 由于 C 2 的半径为1,所以△ C 2 MN 的面积为   . 解法二:直线 C 3 的直角坐标方程为 x - y =0, 圆 C 2 的圆心 C 2 (1,2)到直线 C 3 的距离 d =   =   , 圆 C 2 的半径为1,所以| MN |=2 ×   =   , 所以△ C 2 MN 的面积为   ×   ×   =   . 方法技巧 极坐标方程与直角坐标方程的互化技巧 (1)巧用极坐标方程两边同乘 ρ 或同时平方的技巧,将极坐标方程构造成 含有 ρ cos θ , ρ sin θ , ρ 2 的形式,然后利用互化公式进行转化,最后化简得到 直角坐标方程. (2)巧借两角和差公式,将 ρ sin( θ ± α )= k 或 ρ cos( θ ± α )= k 或 ρ = k sin( θ ± α )或 ρ = k cos( θ ± α )形式的极坐标方程进行转化,进而利用互化公式得到直角坐标 方程. (3)将直角坐标方程中的 x 换成 ρ cos θ , y 换成 ρ sin θ ,即可得到其极坐标方 程. 2-1 　在极坐标系中,已知圆 O : ρ =cos θ +sin θ 和直线 l : ρ sin   =   . (1)求圆 O 和直线 l 的直角坐标方程; (2)当 θ ∈(0,π)时,求直线 l 与圆 O 的公共点的极坐标. 解析 　(1)由 ρ =cos θ +sin θ 可得 ρ 2 = ρ cos θ + ρ sin θ , 把   代入 ρ 2 = ρ cos θ + ρ sin θ 得, 圆 O 的直角坐标方程为 x 2 + y 2 - x - y =0. 由 l : ρ sin   =   ,得 ρ sin θ - ρ cos θ =1, 因为   所以直线 l 的直角坐标方程为 x - y +1=0. (2)由   解得   进而由   解得   因为 θ ∈(0,π),所以 θ =   ,故公共点的极坐标为   . 考点三　极坐标方程及应用 典例3     (2016课标全国Ⅰ,23,10分)在直角坐标系 xOy 中,曲线 C 1 的参数 方程为   ( t 为参数, a >0).在以坐标原点为极点, x 轴正半轴为极 轴的极坐标系中,曲线 C 2 : ρ =4cos θ . (1)说明 C 1 是哪一种曲线,并将 C 1 的方程化为极坐标方程; (2)直线 C 3 的极坐标方程为 θ = α 0 ,其中 α 0 满足tan α 0 =2,若曲线 C 1 与 C 2 的公 共点都在 C 3 上,求 a . 解析 　(1)消去参数 t 得到 C 1 的普通方程: x 2 +( y -1) 2 = a 2 . C 1 是以(0,1)为圆心, a 为半径的圆. 将 x = ρ cos θ , y = ρ sin θ 代入 C 1 的普通方程中,得到 C 1 的极坐标方程为 ρ 2 - 2 ρ sin θ +1- a 2 =0. (2)曲线 C 1 , C 2 的公共点的极坐标满足方程组   若 ρ ≠ 0,由方程组得16cos 2 θ -8sin θ cos θ +1- a 2 =0, 由已知tan θ =2,可得16cos 2 θ -8sin θ cos θ =0,从而1- a 2 =0, 解得 a =-1(舍去)或 a =1. a =1时,极点也为 C 1 , C 2 的公共点,在 C 3 上.所以 a =1. 方法技巧 求曲线的极坐标方程的步骤:(1)建立适当的极坐标系,设 P ( ρ , θ )是曲线上 任意一点;(2)由曲线上的点所适合的条件,列出点 P 的极径 ρ 和极角 θ 之 间的关系式;(3)将列出的关系式进行整理、化简,得出曲线的极坐标方 程. 3-1     (2016河南洛阳统考)已知圆 O 1 和圆 O 2 的极坐标方程分别为 ρ =2, ρ 2 - 2   ρ cos   =2. (1)将圆 O 1 和圆 O 2 的极坐标方程化为直角坐标方程; (2)求经过两圆交点的直线的极坐标方程. 解析　 (1)由 ρ =2,得 ρ 2 =4,所以圆 O 1 的直角坐标方程为 x 2 + y 2 =4. 由 ρ 2 -2   ρ cos   =2, 得 ρ 2 -2   ρ   =2, 所以圆 O 2 的直角坐标方程为 x 2 + y 2 -2 x -2 y -2=0. (2)将两圆的直角坐标方程相减可得经过两圆交点的直线方程,为 x + y =1. 化为极坐标方程为 ρ cos θ + ρ sin θ =1, 即 ρ sin   =   . 3-2     (2016福建福州五校第二次联考)已知曲线 C 的极坐标方程为 ρ 2 - 2   ρ cos   -2=0.以极点为平面直角坐标系的原点,极轴为 x 轴的正半 轴,建立平面直角坐标系 xOy . (1)若直线 l 过原点,且被曲线 C 截得的弦长最短,求直线 l 的直角坐标方程; (2)若 M 是曲线 C 上的动点,且点 M 的直角坐标为( x , y ),求 x + y 的最大值. 解析 　(1) ρ 2 -2   ρ cos   -2=0,即 ρ 2 -2 ρ cos θ +2 ρ sin θ -2=0, 将   代入并整理得曲线 C 的直角坐标方程为( x -1) 2 +( y +1) 2 =4, 其中圆心 C (1,-1),则 k OC =-1.若直线 l 被曲线 C 截得的弦长最短,则直线 l 与 OC 垂直, 即 k l · k OC =-1,因而 k l =1,故直线 l 的直角坐标方程为 y = x . (2)根据 M 是曲线 C 上的动点可设   ( φ 为参数),则 x + y =2sin φ + 2cos φ =2   sin   ,当sin   =1时, x + y 取得最大值2   .