2021届高考数学一轮复习第七章解析几何第2讲两直线的位置关系课件 37页

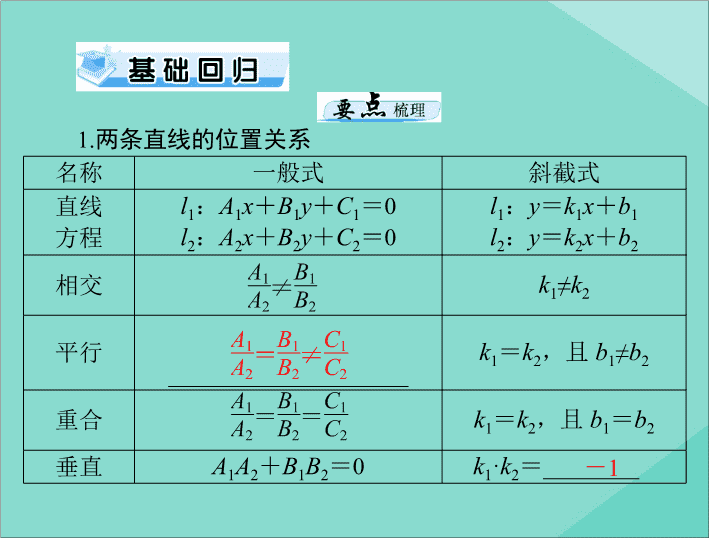
第 2 讲 两直线的位置关系 课标要求 考情风向标 1. 能根据斜率判定两条 直线平行或垂直 . 2. 能用解方程组的方法 求两直线的交点坐标 . 3. 探索并掌握两点间的 距离公式、点到直线的 距离公式，会求两条平 行直线间的距离 1. 求两条直线的位置关系 ( 特别是平行 与垂直 ) 的判定、两点之间的距 离、点到 直线的距离、两条平行线之间的距离是 高考考查的重点，题型既有选择题与填 空题，又有解答题，难度属于中低档题 . 2. 客观题主要以考查基础知识和基本能 力为主，题目较易，主观题主要在知识 的交汇点处命题，全面考查基本概念和 基本能力 名称 一般式 斜截式 直线 方程 l 1 ： A 1 x ＋ B 1 y ＋ C 1 ＝ 0 l 2 ： A 2 x ＋ B 2 y ＋ C 2 ＝ 0 l 1 ： y ＝ k 1 x ＋ b 1 l 2 ： y ＝ k 2 x ＋ b 2 相交 k 1 ≠ k 2 平行 ____________________ k 1 ＝ k 2 ，且 b 1 ≠ b 2 重合 k 1 ＝ k 2 ，且 b 1 ＝ b 2 垂直 A 1 A 2 ＋ B 1 B 2 ＝ 0 k 1 · k 2 ＝ ________ 1. 两条直线的位置关系 － 1 2. 三个距离公式 1. 与直线 3 x － 4 y ＋ 5 ＝ 0 ， 关于 x 轴对称的直线方程为 ______________ ； 关于 y 轴对称的直线方程为 ______________ ； 关于原点对称的直线方程为 ______________ ； 关于直线 y ＝ x 对称的直线方程为 ______________ ； 关于直线 y ＝－ x 对称的直线方程为 ______________. 3 x － 4 y － 5 ＝ 0 3 x ＋ 4 y ＋ 5 ＝ 0 3 x ＋ 4 y － 5 ＝ 0 4 y － 3 y － 5 ＝ 0 4 x － 3 y ＋ 5 ＝ 0 2.(2016 年新课标 Ⅱ ) 圆 x 2 ＋ y 2 － 2 x － 8 y ＋ 13 ＝ 0 的圆心到直 线 ax ＋ y － 1 ＝ 0 的距离为 1 ，则 a ＝ ( ) A 3.(2016 年上海 ) 已知平行直线 l 1 ： 2 x ＋ y － 1 ＝ 0 ， l 2 ： 2 x ＋ y ＋ 1 ＝ 0 ，则 l 1 ， l 2 间的距离为 ________. 4. 已知 A ( － 4,2) ， B (6 ，－ 4) ， C (12,6) ， D (2,12) ，下面四个 结论： ① AB ∥ CD ； ② AB ⊥ AD ； ③ AC ∥ BD ； ④ AC ⊥ BD . 其中正 确的有 ( ) C A.1 个 B.2 个 C.3 个 D.4 个 考点 1 两直线的平行与垂直关系 例 1 ： 已知直线 l 1 ： x ＋ my ＋ 6 ＝ 0 ， l 2 ： ( m － 2) x ＋ 3 y ＋ 2 m ＝ 0 ，求 m 的值，使得： (1) l 1 与 l 2 相交； (2) l 1 ⊥ l 2 ； (3) l 1 ∥ l 2 ； (4) l 1 ， l 2 重合 . 解： (1) 由已知 1×3≠ m ( m － 2) ， 即 m 2 － 2 m － 3≠0 ，解得 m ≠ － 1 ，且 m ≠3. 故当 m ≠ － 1 ，且 m ≠3 时， l 1 与 l 2 相交 . (3) 当 1×3 ＝ m ( m － 2) ， 且 1×2 m ≠6×( m － 2) ， 或 m ×2 m ≠3×6 ，即 m ＝－ 1 时， l 1 ∥ l 2 . (4) 当 1×3 ＝ m ( m － 2) ，且 1×2 m ＝ 6×( m － 2) ， 即 m ＝ 3 时， l 1 与 l 2 重合 . 【 规律方法 】 (1) 充分掌握两直线平行与垂直的条件是解决 本题的关键，对于斜率都存在且不重合的两条直线 l 1 和 l 2 ， l 1 ∥ l 2 ⇔ k 1 ＝ k 2 ， l 1 ⊥ l 2 ⇔ k 1 · k 2 ＝－ 1. 如果有一条直线的斜率不存在， 那么另一条直线的斜率 是多少一定要特别注意 . (2) 设 l 1 ： A 1 x ＋ B 1 y ＋ C 1 ＝ 0 ， l 2 ： A 2 x ＋ B 2 y ＋ C 2 ＝ 0 ，则 l 1 ⊥ l 2 ⇔ A 1 A 2 ＋ B 1 B 2 ＝ 0. 【 跟踪训练 】 1. 已知直线 l 1 ： x ＋ ( a － 2) y － 2 ＝ 0 ， l 2 ： ( a － 2) x ＋ ay － 1 ＝ 0 ， ) 则“ a ＝－ 1” 是“ l 1 ⊥ l 2 ” 的 ( A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要 条件 － 3 ，它们的斜率之积等于－ 1 ，故有 l 1 ⊥ l 2 ，故充分性成立 . 当 l 1 ⊥ l 2 时，有 ( a － 2) ＋ ( a － 2) a ＝ 0 成立，即 ( a － 2)( a ＋ 1) ＝ 0 ，解 得 a ＝－ 1 ，或 a ＝ 2 ，故必要性不成立 . 答案： A 2.(2019 年宁夏模拟 ) 若直线 l 1 ： x ＋ 2 my － 1 ＝ 0 与 l 2 ： (3 m － 1) x － my － 1 ＝ 0 平行，则实数 m 的值为 ________. 时，则 a 的值为 ______. 解析： ∵ 方程有无穷多解，即两直线重合， ∴ 可对 ① ×2 ， 得 4 x ＋ 4 y ＝－ 2. 再与 ② 式比较，可得 a ＝－ 2. － 2 考点 2 直线系中的过定点问题 例 2 ： 求证：不论 m 取什么实数，直线 ( m － 1) x ＋ (2 m － 1) y ＝ m － 5 都通过一定点 . 证明： 方法一，取 m ＝ 1 ，得直线方程 y ＝－ 4 ； 从而得两条直线的交点为 (9 ，－ 4). 又当 x ＝ 9 ， y ＝－ 4 时， 有 9( m － 1) ＋ ( － 4)(2 m － 1) ＝ m － 5 ， 即点 (9 ，－ 4) 在直线 ( m － 1) x ＋ (2 m － 1) y ＝ m － 5 上 . 故直线 ( m － 1) x ＋ (2 m － 1) y ＝ m － 5 都通过定点 (9 ，－ 4). 方法二， ∵ ( m － 1) x ＋ (2 m － 1) y ＝ m － 5 ， ∴ m ( x ＋ 2 y － 1) － ( x ＋ y － 5) ＝ 0. 则直线 ( m － 1) x ＋ (2 m － 1) y ＝ m － 5 都通过直线 x ＋ 2 y － 1 ＝ 0 与 x ＋ y － 5 ＝ 0 的交点 . － 4). ∴ 直线 ( m － 1) x ＋ (2 m － 1) y ＝ m － 5 通过定点 (9 ，－ 4). 方法三， ∵ ( m － 1) x ＋ (2 m － 1) y ＝ m － 5 ， ∴ m ( x ＋ 2 y － 1) ＝ x ＋ y － 5. 由 m 为任意实数知，关于 m 的一元一次方程 m ( x ＋ 2 y － 1) ＝ x ＋ y － 5 的解集为 R ， ∴ 直线 ( m － 1) x ＋ (2 m － 1) y ＝ m － 5 都通过定点 (9 ，－ 4). 【 规律方法 】 本题考查了方程思想在解题中的应用， 构建 方程组求解是解决本题的关键 . 很多学生不理解直线过定点的 含义，找不到解决问题的切入点，从而无法 下手 . 【 跟踪训练 】 4.(2018 年江西临川一中 ) 直线 kx － y ＋ 2 ＝ 4 k ，当 k 变化时， ) 所有直线都通过定点 ( A.(0,0) C.(4,2) B.(2,1) D.(2,4) 解析： 直线方程可化为 k ( x － 4) － ( y － 2) ＝ 0 ， ∴ 直线恒过定 点 (4,2). C 考点 3 对称问 题 考向 1 中心对称 例 3 ： 在平面直角坐标系中，直线 y ＝ 2 x ＋ 1 关于点 (1,1) 对 称的直线方程是 ____________. 解析： 方法一，在直线 l 上任取一点 P ′( x ， y ) ，其关于点 (1,1) 的对称点 P (2 － x, 2 － y ) 必在直线 y ＝ 2 x ＋ 1 上， ∴ 2 － y ＝ 2(2 － x ) ＋ 1 ，即 2 x － y － 3 ＝ 0. 因此，直线 l 的方程为 y ＝ 2 x － 3. 方法二，由题意，得直线 l 与直线 y ＝ 2 x ＋ 1 平行， 设直线 l 的方程为 2 x － y ＋ C ＝ 0( C ≠1) ， 则点 (1,1) 到两平行线的距离相等 . 答案： y ＝ 2 x － 3 考向 2 轴对称 例 4 ： (1) (2019 年广西桂林模拟 ) 点 P (2,5) 关于 x ＋ y ＋ 1 ＝ 0 ) 对称的点的坐标为 ( A.(6,3) C.( － 6 ，－ 3) B.(3 ，－ 6) D.( － 6,3) 答案： C (2)(2017 年广东广州模拟 ) 直线 x － 2 y ＋ 1 ＝ 0 关于直线 x ＋ y ) － 2 ＝ 0 对称的直线方程是 ( A. x ＋ 2 y － 1 ＝ 0 C.2 x ＋ y － 3 ＝ 0 B.2 x － y － 1 ＝ 0 D. x ＋ 2 y － 3 ＝ 0 解析： 由题意得直线 x － 2 y ＋ 1 ＝ 0 与直线 x ＋ y － 2 ＝ 0 的交 点坐标为 (1,1). 在直线 x － 2 y ＋ 1 ＝ 0 上取点 A ( － 1,0) ， 设 A 点关于直线 x ＋ y － 2 ＝ 0 的对称点为 B ( m ， n ) ， 答案： B 【 规律方法 】 轴对称：解决轴对称问题，一般是转化为求 对称点的问题，在求对称点时，关键是抓住两点：一是两对称 点的连线与对称轴垂直；二是两对称点连线的中点在对称轴上， 即抓住 “ 垂直平分 ” ，由 “ 垂直 ” 列出一个方程，由 “ 平分 ” 列出一个方程，联立求解 . 【 跟踪训练 】 5. 光线沿直线 l 1 ： x － 2 y ＋ 5 ＝ 0 射入，遇直线 l ： 3 x － 2 y ＋ 7 ＝ 0 后反射，如图 7-2-1 ，求反射光线所在的直线方程 . 图 7-2-1 考向 3 对称的应用 例 5 ： 在直线 l ： 3 x － y － 1 ＝ 0 上存在一点 P ，使得点 P 到 点 A (4,1) 和点 B (3,4) 的距离之和最小，求此时的距离之和 . 解： 设点 B 关于直线 3 x － y － 1 ＝ 0 的对称点为 B ′( a ， b ) ， 如图 7-2-2. 图 7-2-2 【 跟踪训练 】 6.(2017 年湖南长沙一模 ) 已知入射光线经过点 M ( － 3,4) ， 被直线 l ： x － y ＋ 3 ＝ 0 反射，反射光线经过点 N (2,6) ，则反射光 线所在直线的方程为 ____________ . 6 x － y － 6 ＝ 0 易错、易混、易漏 ⊙ 忽略直线方程斜率不存在的特殊情形致误 例题： 过点 P ( － 1,2) 引一条直线 l ，使它到点 A (2,3) 与到点 B ( － 4,5) 的距离相等，求该直线 l 的方程 . 错因分析： 设直线方程，只要涉及直线的斜率，易忽略斜 率不存在的情形，要注意分类讨论 . 解： 方法一，当直线 l 的斜率不存在时，直线 l ： x ＝－ 1 ， 显然到点 A (2,3) ， B ( － 4,5) 的距离相等 . 当直线 l 的斜率存在时，设斜率为 k ， 则直线 l 的方程为 y － 2 ＝ k ( x ＋ 1) ， 即 kx － y ＋ 2 ＋ k ＝ 0. 【 失误与防范 】 方法一是常规解法，本题可以利用代数方 法求解，即设点斜式方程，然后利用点到直线的距离公式建立 等式求斜率 k ，但要注意斜率不存在的情况，很容易漏解且计 算量较大 . 方法二是利用数形结合的思想使运算量大为减少，即 A ， B 两点到直线 l 的距离相等，有两种情况： ① 直线 l 与 AB 平行； ② 直线 l 过线段 AB 的中点 . 1. 两直线的位置关系要考虑平行、垂直和重合 . 对于斜率都 存在且不重合的两条直线 l 1 ， l 2 ， l 1 ∥ l 2 ⇔ k 1 ＝ k 2 ； l 1 ⊥ l 2 ⇔ k 1 · k 2 ＝ － 1. 根据两直线的方程判断两直线的位置关系时，要特别注意 斜率是否存在，对于斜率不存 在的情况要单独考虑 . 注意斜率相 等并不是两直线平行的充要条件，斜率互为负倒数也不是两直 线垂直的充要条件 . 2. 直线系 . (1) 与直线 Ax ＋ By ＋ C ＝ 0 平行的直线系方程为 Ax ＋ By ＋ C ′ ＝ 0 ； (2) 与直线 Ax ＋ By ＋ C ＝ 0 垂直的直线系方程为 Bx － Ay ＋ C ′ ＝ 0; (3) 过两直线 l 1 ： a 1 x ＋ b 1 y ＋ c 1 ＝ 0 ， l 2 ： a 2 x ＋ b 2 y ＋ c 2 ＝ 0 的交 点的直线系方程为 a 1 x ＋ b 1 y ＋ c 1 ＋ λ ( a 2 x ＋ b 2 y ＋ c 2 ) ＝ 0.( λ 为参数 ) 3. 对称问题包括中心对称和轴对称两种情形，其中，中心 对称一般是中点坐标公式的应用 . 轴对称一般要用到中点坐标 公式和斜率公式 ( 垂直 ). 光线的反射问题具有入射角等于反射角 的特点，这 样就有两种对称关系： (1) 入射光线与反射光线关于过反射点且与反射轴垂直的 直线 ( 法线 ) 对称； (2) 入射光线与反射光线所在直线关于反射轴对称 .