云南师范大学附属中学呈贡校区2020—2021学年高二上学期第一学段模块考试试题（期中考试） 7页

高二文科数学 第 1 页 共 7 页 云南师大附中呈贡校区 2020—2021 学年上学期第一 学段模块考试试题（期中考试） 高二年级文科数学学科模块《必修三》 一、选择题：本题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个 选项中，只有一项是符合题目要求的． 1． 在一次数学考试中，高二理 8 班 56 名同学的成绩的茎叶图如图所示， 9 8 7 6 5 0 0 4 0 0 3 4 5 5 5 6 6 6 7 7 7 9 9 0 0 1 1 1 2 2 5 5 7 7 8 9 9 1 3 4 4 4 4 5 6 8 9 9 9 0 0 0 5 5 6 6 7 8 9 9 9 若将同学的成绩由高分到低分编为 1~56 号，再用系统抽样从中抽取 7 人，则成绩在区间[70，86]的人数是 A．2 B．3 C．4 D．5 2．设一组样本数据 的方差为 0.05，则数据 的方 差为 A．0.05 B．0.5 C．5 D．50 3．命题“对任意 ，都有 ”的否定为 A．对任意 ，都有 B．不存在 ，都有 C．存在 ，使得 D．存在 ，都有 4．函数 的图像向右平移 1 个单位长度，所得图像与曲线 关于 轴对称，则 A． B． C． D． 1 2, , , nx x x 1 210 ,10 , ,10 nx x x Rx∈ 0x ≥ Rx∈ 0x < Rx∈ 0x < 0 Rx ∈ 0 0x ≥ 0 Rx ∈ 0 0x < ( )f x exy = y ( )f x = 1ex+ 1ex− 1e x− + 1e x− − 高二文科数学 第 2 页 共 7 页 5．某次辩论赛中共有 7 位评委，评定选手的成绩时，从 7 位评委给出的原 始评分中去掉 1 个最高分、1 个最低分，得到 5 个有效评分．5 个有效评 分和 7 个原始评分相比，不变的数字特征是 A．中位数 B．平均数 C．方差 D．极差 6．已知变量 和 满足关系 ，变量 与 负相关．下列结论正确 的是 A． 与 负相关， 与 负相关 B． 与 负相关， 与 正相关 C． 与 正相关， 与 负相关 D． 与 正相关， 与 正相关 7．今年学校的体育节将于 12 月 3 日~5 日举行，某班的甲、乙两名同学各 自等可能的从 100 米、200 米和跳远三项运动项目中选择 2 项报名参赛， 则他们选择的两项运动项目都相同的概率为 A． B． C． D． 8．双曲线 的一个焦点 到一条渐近线的距离等于 焦距的 ，则 的离心率为 A． B． C． D． 9．点 到直线 的距离的最大值为 A．1 B． C． D． 10．已知等比数列 的公比为 ，前 项和为 ，则 是 的 A．必要不充分条件 B．充分不必要条件 C．充分必要条件 D．既不充分也不必要条件 x y 2 1y x= + y z x y x z x y x z x y x z x y x z 1 3 2 3 1 2 1 9 2 2 2 2: 1( 0, 0)x yC a ba b − = > > F 1 4 C 2 3 2 2 3 2 4 2 3 3 (0, 1)− ( 2) ( 1) ( 2) 0m x m y m+ + − + + = 2 3 2 { }na q n nS 0q > 1n nS S+ > 高二文科数学 第 3 页 共 7 页 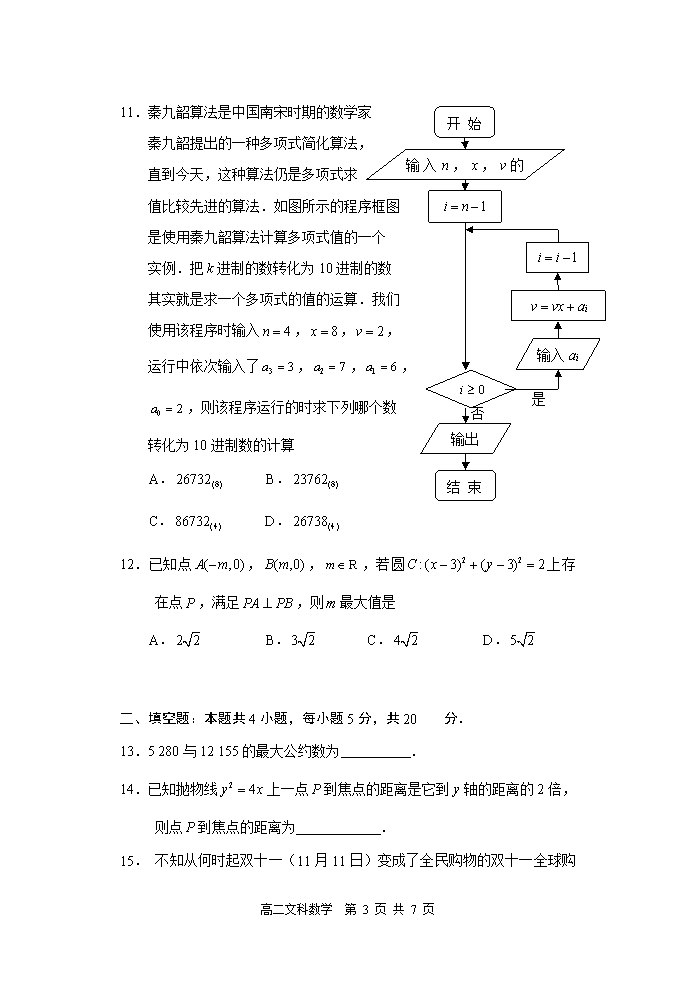11．秦九韶算法是中国南宋时期的数学家 秦九韶提出的一种多项式简化算法， 直到今天，这种算法仍是多项式求 值比较先进的算法．如图所示的程序框图 是使用秦九韶算法计算多项式值的一个 实例．把 k 进制的数转化为 10 进制的数 其实就是求一个多项式的值的运算．我们 使用该程序时输入 ， ， ， 运行中依次输入了 ， ， ， ，则该程序运行的时求下列哪个数 转化为 10 进制数的计算 A． B． C． D． 12．已知点 ， ， ，若圆 上存 在点 ，满足 ，则 最大值是 A． B． C． D． 二、填空题：本题共 4 小题，每小题 5 分，共 20 分． 13．5 280 与 12 155 的最大公约数为 ． 14．已知抛物线 上一点 到焦点的距离是它到 轴的距离的 2 倍， 则点 到焦点的距离为 ． 15． 不知从何时起双十一（11 月 11 日）变成了全民购物的双十一全球购 4n = 8x = 2v = 3 3a = 2 7a = 1 6a = 0 2a = (8)26732 (8)23762 (4)86732 (4)26738 ( ,0)A m− ( ,0)B m Rm∈ 2 2:( 3) ( 3) 2C x y− + − = P PA PB⊥ m 2 2 3 2 4 2 5 2 2 4y x= P y P 开 始 输 入 ， ， 的 值 n x v 1i n= − 0i ≥ 输入 ai aiv vx= + 1i i= − 输出 v 结 束 是 否 高二文科数学 第 4 页 共 7 页 物节，2019 年 11 月 12 日中国人民银行通过微信公众号宣布，双十一 期间共处理网络支付业务 11.79 亿笔、金额 14820.7 亿元，即全国人民 人均 1 单，人均花费 1000 元． 某公司对某地区 10 000 名 在 2019 年双十一期间网络 购物者的消费情况进行统 计，发现消费金额都在区 间 （单位：万元） 内，其频率分布直方图如图所示，根据频率分布直方图所给数据，估计 该地区购物者在双十一期间的平均消费额为 万元（同一组中的 数据用该组区间的中点值为代表）． 16． “全国部分大学附中教学协作体”成立于 1991 年，由湖南师大附中， 福建师大附中，陕西师大附中，南开大学附中，辽宁师大附中和云南 师大附中在长沙发起年会倡议，九十年代末期首都师大附中和山东师 大附中相继加盟．今年 10 月协作体第二十九届年会在我校举行，在年 会联谊会的舞台左右两端分别挂有两串彩灯，这两串彩灯的第一次闪 亮是相互独立的，且都在通电后 4 秒内的任一时刻等可能的闪亮．那 么在两串彩灯同时通电后，它们第一次闪亮的时刻相差不超过 2 秒的 概率为 ． 二、解答题：共 70 分．解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分 10 分） 记 为等差数列 的前 项和，已知 ， . （1）求 的通项； [0.3,0.9] nS }{ na n 112 31 =+ aa 255 =S }{ na 0 0.5 1 1.5 2 2.5 3 3.5 1 2 3 4 5 6 坐 标 轴 标 题 坐标轴标题 图表标题 0.3 0.4 0.5 0.6 0.7 0.8 0.9 金额/万元 a 2.5 2.0 1.5 0.8 0.2 频率 组距 高二文科数学 第 5 页 共 7 页 （2）设 ，求 的前 项和 .n n n ab 1)2( −−= }{ nb n nT 高二文科数学 第 6 页 共 7 页 18．（本小题满分 12 分） 已 知 的 内 角 所 对 的 边 分 别 为 ， 且 . （1）求角 的大小； （2）若 ， 边上的中线 的长为 ，求 的面积. 19．（本小题满分 12 分） 如图，圆柱的轴截面 是正方形，点 是底面圆周上异于 的一点， ， 是垂足. （1）证明： ； （2）若 ，当三棱锥 体积 最大时，求点 到平面 的距离. 20．（本小题满分 12 分） 国家统计局浙江调查总队 2019 年 3 月 4 日公布了《历年城乡居民家庭 人均收入情况》（1978——2018），其中 2010 年至 2018 年该地区城镇居民家 庭人均可支配收入 y（单位：万元）如下表所示 年份 201 0 201 1 201 2 201 3 201 4 201 5 201 6 201 7 201 8 年份代号 t 1 2 3 4 5 6 7 8 9 人均可支配 收入 y 2.7 3.1 3.5 3.7 4.1 4.4 4.7 5.1 5.6 （1）求 y 关于 t 的线性回归方程； （2）利用（1）中的回归方程，分析 2010 年至 2018 年该地区城镇居 民家庭人均纯收入的变化情况，并预测该地区 2020 年城镇居民 家庭人均纯收入． 附：回归直线的斜率和截距的最小二乘法估计公式分别为 ， ． ABC∆ CBA ,, cba ,, )3sin(23 π+= Cab A 3=AC AB CD 7 ABC∆ ABCD E BA, DEAF ⊥ F DBAF ⊥ 2=AB ABED − C BDE 1 2 1 ( )( ) ˆ ( ) n i i i n i i t t y y b t t = = − − = − ∑ ∑ ˆˆa y bt= − 高二文科数学 第 7 页 共 7 页 21．（本小题满分 12 分） 全美数学竞赛（American Mathematics Competition， 简称 AMC）共有 25 道选择题，每题 6 分，共 150 分．每道题有 A，B，C，D，E 共 5 个选 项，只有一个正确选项．评分规则为：填写正确答案得 6 分，不填得 2 分， 填错答案得 0 分．某考生考试快结束时，还余下 2 道题没有完成．若该考生 随机选中 5 个选项中的某一个和不填这 6 种情况是等可能的． （1）求他这 2 题恰好得到 2 分的概率； （2）如果这 2 道题中，每道题均可随机猜一个答案填写或者不填，请从 小到大列举出所有可能的得分． 22．（本小题满分 12 分） 已 知 椭 圆 的 上 顶 点 为 ， 离 心 率 . （1）求椭圆 的方程； （2）设不过点 的直线 与椭圆 交于 两点，满足： ，求 面积的最大值. )0(1: 2 2 2 2 >>=+ bab y a xC )2,0(P 3 6=e C P l C BA, PBPA ⊥ PAB∆