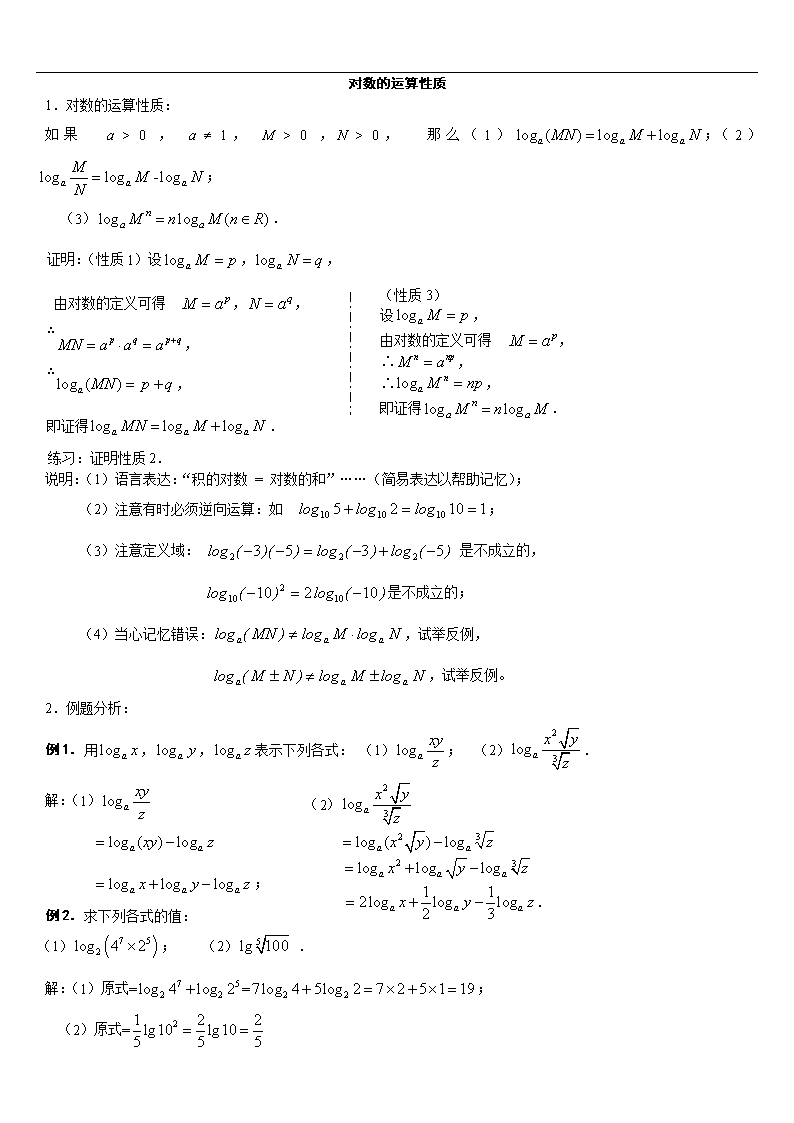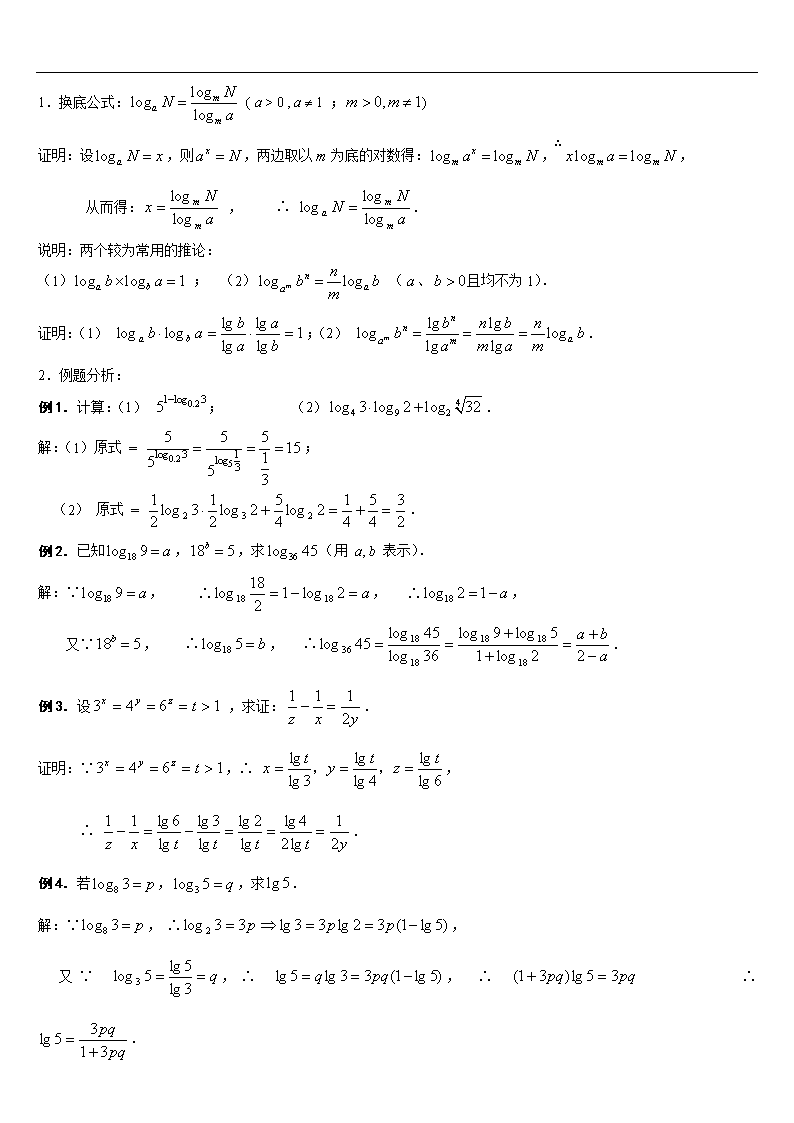高考数学专题复习（精选精讲）练习2-对数函数习题精选精讲 13页

对数的运算性质 ‎1．对数的运算性质：‎ 如果 a > 0 ， a ¹ 1， M > 0 ，N > 0， 那么（1）；（2）；‎ ‎（3）．‎ 证明：（性质1）设，， ‎ ‎（性质3）‎ 设，‎ 由对数的定义可得 ，‎ ‎∴，‎ ‎∴，‎ 即证得．‎ ‎ 由对数的定义可得 ，，‎ ‎∴，‎ ‎∴，‎ 即证得．‎ 练习：证明性质2．‎ 说明：（1）语言表达：“积的对数 = 对数的和”……（简易表达以帮助记忆）；‎ ‎（2）注意有时必须逆向运算：如 ；‎ ‎（3）注意定义域： 是不成立的，‎ ‎ 是不成立的；‎ ‎（4）当心记忆错误：，试举反例， ‎ ‎ ，试举反例。‎ ‎2．例题分析：‎ 例1．用，，表示下列各式： ‎（2）‎ ‎．‎ （1）； （2）．‎ 解：（1）‎ ‎；‎ 例2．求下列各式的值：‎ ‎（1）； （2） ．‎ 解：（1）原式==；‎ ‎（2）原式=‎ 例3．计算：（1）lg1421g； （2）； （3）．‎ 解：（1）解法一：‎ ‎；‎ 解法二：=；‎ 说明：本例体现了对数运算性质的灵活运用，运算性质常常逆用，应引起足够的重视。‎ ‎（2）；‎ ‎（3）=．‎ 例4．已知，，求的值。‎ 分析：此题应注意已知条件中的真数2，3，与所求中的真数有内在联系，故应将1.44进行恰当变形：，然后应用对数的运算性质即可出现已知条件的形式。‎ 解： ．‎ 说明：此题应强调注意已知与所求的内在联系。‎ 例5．已知，求．‎ 分析：由于是真数，故可直接利用对数定义求解；另外，由于等式右端为两实数和的形式，的存在使变形产生困难，故可考虑将移到等式左端，或者将变为对数形式。‎ 解：（法一）由对数定义可知：．‎ ‎（法二）由已知移项可得，即，由对数定义知：，∴ ．‎ ‎（法三），∴，∴ ．‎ 说明：此题有多种解法，体现了基本概念和运算性质的灵活运用，可以对于对数定义及运算性质的理解。‎ 例6．（1）已知，用a表示；（2）已知，，用、表示 ．‎ 解：（1）∵，∴， ∴ log 3 4 - log 3 6 = ．‎ ‎（2）∵， ∴， ‎ 又∵，∴=．‎ 换底公式 ‎1．换底公式： ( a > 0 , a ¹ 1 ；)‎ 证明：设，则，两边取以为底的对数得：，∴，‎ 从而得： ， ∴ ．‎ 说明：两个较为常用的推论：‎ ‎（1） ； （2） （、且均不为1）．‎ 证明：（1） ；（2） ．‎ ‎2．例题分析：‎ 例1．计算：（1） ； （2）． ‎ 解：（1）原式 = ；‎ ‎ （2） 原式 = ．‎ 例2．已知，，求（用 a, b 表示）．‎ 解：∵， ∴， ∴，‎ 又∵， ∴， ∴．‎ 例3．设 ，求证：．‎ 证明：∵，∴ ，‎ ‎ ∴ ．‎ 例4．若，，求．‎ 解：∵， ∴，‎ ‎ 又∵ ，∴ ， ∴ ∴ ．‎ 例5．计算：．‎ 解：原式 ‎ ‎ ．‎ 例6．若 ，求．‎ 解：由题意可得：， ∴，∴．‎ 对数函数 例1．求下列函数的定义域：‎ ‎（1）； （2）； （3）．‎ 分析：此题主要利用对数函数的定义域求解。‎ 解：（1）由>0得，∴函数的定义域是；‎ ‎（2）由得，∴函数的定义域是；‎ ‎（3）由9-得-3，∴函数的定义域是．‎ 说明：此题只是对数函数性质的简单应用，应强调学生注意书写格式。‎ 例2．求函数和函数的反函数。‎ 解：（1） ∴ ；‎ ‎ （2） ∴ ．‎ 例4．比较下列各组数中两个值的大小：‎ ‎ （1），； （2），； （3），.‎ 解：（1）对数函数在上是增函数，‎ 于是；‎ ‎（2）对数函数在上是减函数，‎ 于是；‎ ‎（3）当时，对数函数在上是增函数，‎ 于是，‎ ‎ 当时，对数函数在上是减函数，‎ 于是．‎ 例5．比较下列比较下列各组数中两个值的大小：‎ ‎（1），； （2），； ‎ ‎（3），，； （4），，．‎ 解：（1）∵， ，∴；‎ ‎ （2）∵， ，∴．‎ ‎ （3）∵， ， ，‎ ‎∴．‎ ‎ （4）∵， ∴．‎ 例6．已知，比较，的大小。‎ 解：∵， ∴，当，时，得，‎ ‎∴， ∴．当，时，得，‎ ‎∴， ∴．当，时，得，，‎ ‎∴，， ∴．‎ 综上所述，，的大小关系为或或．‎ 例7．求下列函数的值域：‎ ‎（1）；（2）；（3）（且）．‎ 解：（1）令，则， ∵， ∴，即函数值域为．‎ ‎ （2）令，则， ∴， 即函数值域为．‎ ‎ （3）令， 当时，， 即值域为，‎ ‎ 当时，， 即值域为．‎ 例8．判断函数的奇偶性。‎ 解：∵恒成立，故的定义域为， ‎ ‎，所以，为奇函数。‎ 例9．求函数的单调区间。‎ 解：令在上递增，在上递减，‎ 又∵， ∴或，‎ 故在上递增，在上递减， 又∵为减函数，‎ 所以，函数在上递增，在上递减。‎ 说明：利用对数函数性质判断函数单调性时，首先要考察函数的定义域，再利用复合函数单调性的判断方法来求单调区间。‎ 例10．若函数在区间上是增函数，的取值范围。‎ 解：令， ∵函数为减函数，‎ ‎∴在区间上递减，且满足，∴，解得，‎ 所以，的取值范围为．‎ 对数函数 ‎1 如图，曲线是对数函数 的图象，已知 的取值 ，则相应于曲线 的 值依次为(    )．‎ ‎　　（A）  ‎ ‎　　（B）            ‎ ‎　　（C） ‎ ‎　　（D） ‎ ‎2.函数y=logx－1(3－x)的定义域是 ‎ 如果对数有意义，求x的取值范围；‎ 解：要使原函数有意义，则 解之得： ‎ ‎∴原函数的定义域为-7，-6)(-6，-5) (-1，+)‎ 函数的定义域为一切实数，求k的取值范围。‎ 利用图像判断方程根的个数 ‎3．已知关于的的方程，讨论的值来确定方程根的个数。‎ 解：因为在同一直角坐标系中作出函数与的图象，如图可知：①当时，两个函数图象无公共点，所以原方程根的个数为0个；‎ ‎②当时，两个函数图象有一个公共点，所以原方程根的个数为1个；‎ ‎③当时，两个函数图象有两个公共点，所以原方程根的个数为2个。‎ ‎4．若关于的方程的所有解都大于1，求的取值范围．‎ 解：由原方程可化为 ‎，变形整理有 ‎（*）‎ ‎，，由于方程（*）的根为正根，则 解之得，从而 ‎5．求函数的单调区间．‎ ‎．解：设，，由得，知定义域为 又，则当时，是减函数；当时，是增函数，而在上是减函数 的单调增区间为，单调减区间为 题目2】求函数的单调区间。‎ 正解】由得x＜1或x＞5，即函数的定义域为{x| x＜1或x＞5}，‎ 当x＜1时，是减函数，是减函数，所以是增函数；‎ 当x＞5时，是增函数，是减函数，所以是减函数；‎ 所以的增区间是（-∞，1）；减区间是（5，∞，）。‎ ‎6、设函数 ，若 的值域为 ，求实数 的取值范围．‎ ‎　　分析：由值域为 和对数函数的单调性可将问题转化为 能取遍所有正实数的问题．‎ ‎　　解： 令 ，依题意 应取遍一切正实数即函数值域是正实数集的子集．则有 或 ，解得 ．‎ 已知函数f(x)=lg［(a2－1)x2+(a+1)x+1］.‎ ‎(1)若f(x)的定义域为R，求实数a的取值范围；‎ ‎(2)若f(x)的值域为R，求实数a的取值范围.‎ 解：(1)(a2－1)x2+(a+1)x+1＞0对x∈R恒成立.‎ a2－1=0时，a=±1，经检验a=－1时恒成立；‎ a2－1≠0时， ‎ a＜－1或a＞ ，‎ ‎∴a≤－1或a＞ .‎ ‎(2)a2－1=0，即a=1时满足值域为R；‎ a2－1≠0时， ‎ ‎1＜a≤ .‎ ‎∴1≤a≤ .‎ ‎7的定义域为R，求a的取值范围。‎ ‎【正解】①当a=0时，y=0，满足条件，即函数y=0的定义域为R；‎ ‎②当a≠0时，由题意得：；‎ 由①②得a的取值范围为[0，4）。‎ ‎【评注】参数问题，分类要不重不漏，对于不等式不一定是一元二次不等式。‎ ‎8.函数y=log［(1－x)(x+3)］的递减区间是( )‎ A.(－3,－1) B.(－∞,－1) C.(－∞,－3) D.(－1，＋∞)‎ ‎【解析】设t＝(1－x)(x＋3)＝－x2－2x＋3＝－(x＋1)2＋4由(1－x)(x＋3)＞0得－3＜x＜1当x∈(－3，－1)时，t＝(1－x)(x＋3)递增∴y＝log［(1－x)(x＋3)］的递减区间是(－3，－1)‎ ‎9.已知函数y＝loga(2－ax)在［0，1］上是x的减函数，则a的取值范围是( )‎ A.0＜a＜1 B.a＞‎1 ‎‎ C.1＜a＜2 D.1＜a≤2‎ ‎【解析】若0＜a＜1，则函数在定义域上是增函数；若a＞1，则当0≤x≤1时，2－ax＞0恒成立即x＜，因此＞1∴1＜a＜2‎ ‎10.求函数y=loga(2-ax-a2x)的值域。‎ ‎【解】由于2-ax-a2x>0，得-21时，y=logat递增，∴yloga2。‎ 故当a>1时，所求的值域为（-∞，loga2）；当0