七年级数学上册第2章代数式章末复习课件 湘教版 28页

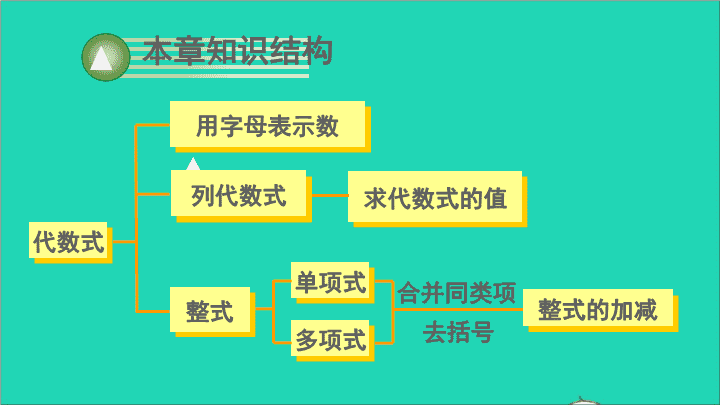
章末复习 本章知识结构 用字母表示数 列代数式 整式 整式的加减 代数式 求代数式的值 单项式 多项式 合并同类项 去括号 回顾 1.请举出用字母表示数的实例。 已知“天宫一号”大约每小时绕地球飞 行2.844万千米，则它飞行th，那么它飞行了 2.844t万千米。 2. 什么叫代数式？列代数式时，一般怎么规 范书写？如何求代数式的值？ 把数与表示数的字母用运算符号连接而成的 式子叫做代数式。 用字母表示式子时应注意: 1.在含有字母的式子里，数字和字母，字母 和字母中间的乘号可以记作“·”，也可以省略不写 。省略乘号时，一般把数字写在字母的前面。 2.两个相同字母相乘时，写成乘方的形式。 3.当数字1与字母相乘时，1也省略不写。 代入一个a值 得出一个结果 做一做 1、某产品的成本由x元下降10%后是 ____________元. 2、一个长方形的周长为m，宽为a，则该长 方形的长为________。 （1–10% ）x m a2  3、若a+b=4，那么 _____ 。a b =a b 14 2     3 回顾 3. 什么叫单项式、多项式？单独一个数或 字母是单项式吗？单项式的次数、多项式的次数 分别是如何确定的？ 由数字与字母的积组成的代数式叫做单项式。 由几个单项式的和组成的代数式叫做多项式。 单独一个字母或者一个数也是单项式。 一个单项式中，所有字母的指数的和叫 做这个单项式的次数。 多项式中次数最高的项的次数，叫做这 个多项式的次数。 做一做 1、在式 子： ， ， ， ， ，a 2 a 3 1–x–5xy2，–x中，哪些是单项式，哪些是多项式？ 哪些是整式？ x y 1  x y 2  y21 2  单项式有 ， ，–xa 3 y21 2  多项式有 ，1–x–5xy2 x y 2  整式 ， ，–x， ， 1–x–5xy2 a 3 y21 2  x y 2  2、 的系数是（ ），次数是 （ ）， 的系数是（ ），次数是（ ）。 y21 2  a 3 1 3 1 3、 的项是（ ），次数是（ ）， 1–x–5xy2的项是（ ），次数是 （ ），是（ ）次（ ）项式. x y 2  1 2  2 2 x y-、 2 1 1、–x、–5xy2 3 3 3 回顾 4. 什么叫同类项？怎样合并同类项？ xy1 3 xy1 3 同类项合并过程中，把同类项的系数相加， 字母和字母的指数不变。不是同类项不可以合并。 1、下列各组是不是同类项： 做一做 （1）4abc 与 4ab （2）–5 m2 n3 与 2n3 m2 （3）–0.3 x2 y 与 y x2 不是 是 是 2、合并下列同类项： （1）3xy – 4 xy – xy = （ ） （2）– a – a – 2a=（ ） （3）0.8ab3 – a3 b+0.2ab3 =（ ） –2xy –4a ab3–a3b 回顾 5、去括号的法则是什么？ 括号前是“+”号，运用加法结合律把括 号去掉，原括号里各项的符号都不变. 括号前是“–”号，把括号和它前面的 “–”号去掉，原括号里各项的符号都要改变。 1、去括号:（1）+（x－3）= （2）－（x－3）= （3）－（x+5y－2）= （4）+（3x－5y+6z）= 做一做 x–3 – x+3 – x – 5y+2 3x – 5y+6z 2、计算:（1）x－（－y －z+1）=___________； （2）m+（－n+q）=____________； （3）a － （b+c－3）=____________； （4）x+（5－3y）=___________. x+y +z –1 m－n+q a－b－c+3 x+5－3y 航行问题 一条河流的水流速度是x千米/秒，已知轮船 在静水中的速度是y千米/秒，则轮船在这条河流中 顺水行驶和逆水行驶的速度分别怎样表示？ 解：当船顺水行驶时，船的速度是（x+y） 千米/秒，当船逆水行驶时，船的速度是（x–y） 千米/秒 船在河流中行驶时，需要分两种情况讨论： 顺水行驶： 船的速度=船在静水中的速度+水流的速度 逆水行驶： 船的速度=船在静水中的速度-水流的速度 典型例题 1.做大小两个长方体纸盒，尺寸如下（单 位：cm）： a b c 2a 3b 4c （1）做这两个纸盒共用料多少平方厘米？ 解：小纸盒的表面积是：（2ab+2bc+2ac）cm2 大纸盒的表面积是： 2×2a×3b+2×3b×4c+2×2a×4c =（12ab+24bc+16ac）cm2 共用料：（2ab+2bc+2ac）+（12ab+24bc+16ac） = 14ab+26bc+18ac （cm2） （2）做大纸盒比做小纸盒多用料多少平方厘米？ （12ab+24bc+16ac）–（2ab+2bc+2ac） = 10ab+22bc+14ac （cm2） （2）5a2 －[a2+(5 a2 －2a) －2(a2 －3a)] （1） 3(xy2－x2y) －2(xy+xy2)+3x2y； 2.计算 = 3xy2－3x2y －2xy － 2xy2+3x2y = xy2 － 2xy = 5a2 －a2 － 5a2 +2a+2a2 －6a = a2 － 4a xy x x xy2 26 [3 2( 2 ) 1]    其中 x = – 1 ，y = 2 3. 解 6xy – [3x2–2（x2–2xy）+1] = 6xy–3x2+2x2–4xy–1 = –x2+ 2xy –1 当 x = – 1 ，y = 2时， 原式= –（–1）2+2×（–1 ）×2–1= –6 4.已知 ， ，求 。A x y2  B x y3 5  A B5 解 A+5B =（x+2y）+5（3x–5y） = x+2y+15x–25y = 16x–23y 5.观察下列图形中火柴棒的摆放方式。 ③②① 梯形个数 1 2 3 4 5 火柴棒根数 （1）填写下表 ： 5 9 13 17 21 （2）照这样的规律搭下去，搭n个这样的三 角形需要多少根火柴棒？ 4n+1