2019七年级数学上册 2等式的基本性质 3页

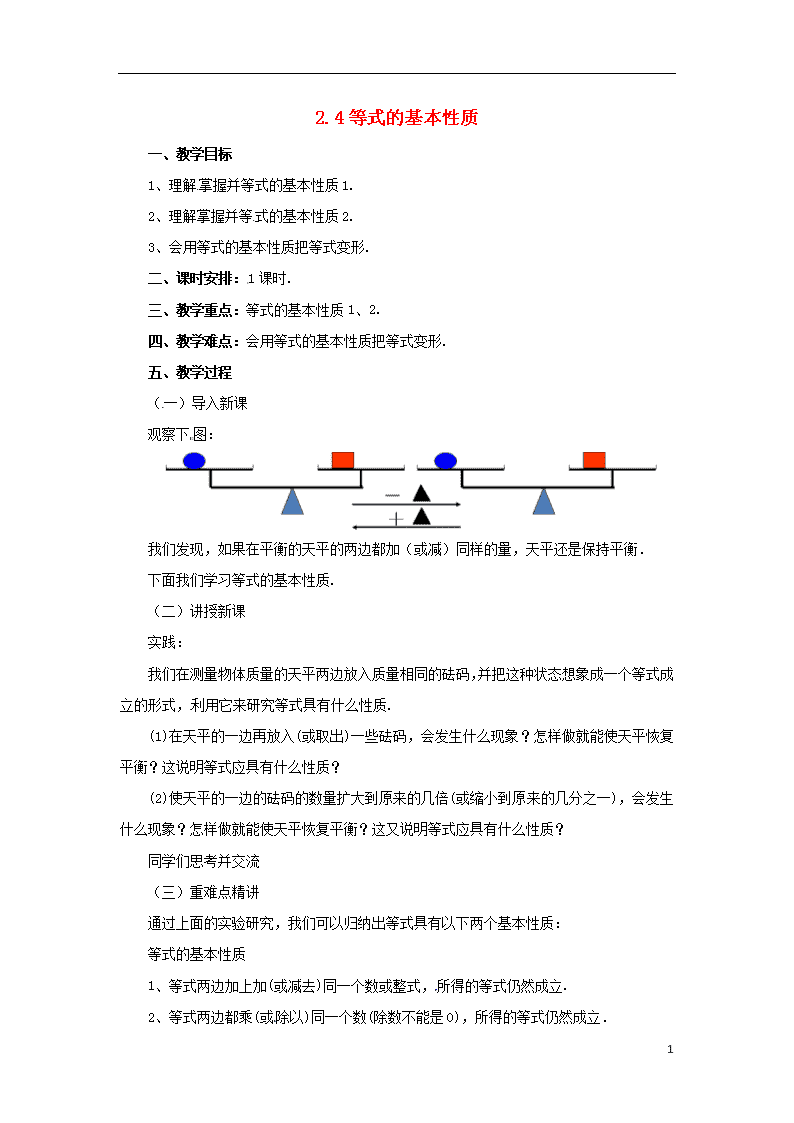
‎2.4等式的基本性质 一、教学目标 ‎1、理解掌握并等式的基本性质1.‎ ‎2、理解掌握并等式的基本性质2.‎ ‎3、会用等式的基本性质把等式变形.‎ 二、课时安排：1课时.‎ 三、教学重点：等式的基本性质1、2.‎ 四、教学难点：会用等式的基本性质把等式变形.‎ 五、教学过程 ‎（一）导入新课 观察下图：‎ 我们发现，如果在平衡的天平的两边都加（或减）同样的量，天平还是保持平衡．‎ 下面我们学习等式的基本性质.‎ ‎（二）讲授新课 实践：‎ 我们在测量物体质量的天平两边放入质量相同的砝码，并把这种状态想象成一个等式成立的形式，利用它来研究等式具有什么性质.‎ ‎(1)在天平的一边再放入(或取出)一些砝码，会发生什么现象？怎样做就能使天平恢复平衡？这说明等式应具有什么性质？‎ ‎(2)使天平的一边的砝码的数量扩大到原来的几倍(或缩小到原来的几分之一)，会发生什么现象？怎样做就能使天平恢复平衡？这又说明等式应具有什么性质？‎ 同学们思考并交流 ‎（三）重难点精讲 通过上面的实验研究，我们可以归纳出等式具有以下两个基本性质：‎ 等式的基本性质 ‎1、等式两边加上加(或减去)同一个数或整式，所得的等式仍然成立.‎ ‎2、等式两边都乘(或除以)同一个数(除数不能是0)，所得的等式仍然成立．‎ 3‎ 我们可以用数学式子表示等式的基本性质：‎ ‎1、如果a=b，c表示任意的数或整式，那么a+c=b+c.‎ ‎2、如果a=b，c表示任意的数，那么ac=bc；‎ 如果a=b，c≠0，那么.‎ 典例：‎ 例、用适当的数或式子填空，使得到的结果仍是等式，并说明是根据等式的哪条基本性质及怎样变形(改变式子的形状)的.‎ ‎(1)如果3x=7-5x，那么3x+_______=7.‎ ‎(2)如果，那么x=_______.‎ 解：(1)3x+5x=7.‎ 根据等式的基本性质1，在等式的两边都加上5x.‎ ‎(2)x=.‎ 根据等式的基本性质2，在等式的两边同时乘.‎ 跟踪训练：‎ 用适当的数或式子填空，使得到的结果仍是等式，并说明是根据等式的哪条基本性质及怎样变形(改变式子的形状)的.‎ ‎(1)如果2x=6-3x，那么3x+_______=7.‎ ‎(2)如果，那么y=_______.‎ 解：(1)3x+3x=6.‎ 根据等式的基本性质1，在等式的两边都加上5x.‎ ‎(2)y=-8.‎ 根据等式的基本性质2，在等式的两边同时乘-4.‎ ‎（四）归纳小结 通过这节课的学习，你有哪些收获？有何感想？学会了哪些方法？先想一想，再分享给大家．‎ ‎（五）随堂检测 ‎1、根据等式的性质，方程5x－1＝4x变形正确的是(　　)‎ 3‎ A．5x＋4x＝－1　　　　B. x－＝2x C．5x－4x＝－1 D．5x＋4x＝1‎ ‎2、下列四组变形中，变形正确的是(　　)‎ A．由5x＋7＝0，得5x＝－7‎ B．由2x－3＝0，得2x－3＋3＝0‎ C．由＝2，得x＝‎ D．由5x＝7，得x＝35‎ ‎3、用适当的数或式子填空，使所得的结果仍是等式，并说明根据哪一条性质以及怎样变形的．‎ ‎(1)若2x＋7＝10，则2x＝10－7.‎ 根据等式的性质____，等式两边同时 ；‎ ‎(2)若－3x＝－18，则x＝ ．‎ 根据等式的性质____，等式两边同时____________________.‎ ‎(3)若3(x－2)＝－6，则x－2＝ ．‎ 根据等式的性质____，等式两边同时 ，所以x＝ ．‎ 六、板书设计 ‎§2.4等式的基本性质 等式的基本性质1：‎ 等式的基本性质2：‎ 例1、‎ 七、作业布置：课本P84 练习 1、2‎ 八、教学反思 3‎