探索三角形全等的条件教案 4页

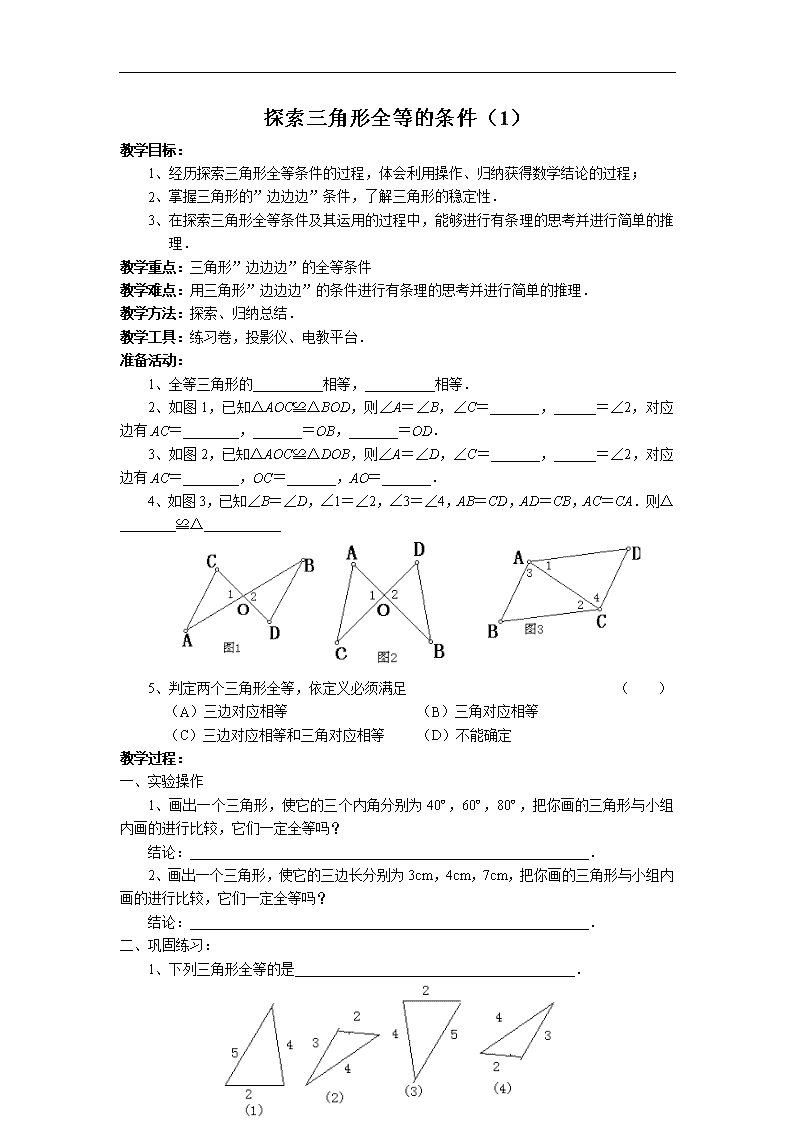
‎ ‎ 探索三角形全等的条件（1）‎ 教学目标：‎ ‎1、经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程；‎ ‎2、掌握三角形的”边边边”条件，了解三角形的稳定性．‎ ‎3、在探索三角形全等条件及其运用的过程中，能够进行有条理的思考并进行简单的推理．‎ 教学重点：三角形”边边边”的全等条件 教学难点：用三角形”边边边”的条件进行有条理的思考并进行简单的推理．‎ 教学方法：探索、归纳总结．‎ 教学工具：练习卷，投影仪、电教平台．‎ 准备活动：‎ ‎1、全等三角形的__________相等，__________相等．‎ ‎2、如图1，已知△AOC≌△BOD，则∠A＝∠B，∠C＝_______，______＝∠2，对应边有AC＝________，_______＝OB，_______＝OD．‎ ‎3、如图2，已知△AOC≌△DOB，则∠A＝∠D，∠C＝_______，______＝∠2，对应边有AC＝________，OC＝_______，AO＝_______．‎ ‎4、如图3，已知∠B＝∠D，∠1＝∠2，∠3＝∠4，AB＝CD，AD＝CB，AC＝CA．则△________≌△___________‎ ‎5、判定两个三角形全等，依定义必须满足 （　　）‎ ‎（A）三边对应相等 （B）三角对应相等 ‎（C）三边对应相等和三角对应相等 （D）不能确定 教学过程：‎ 一、实验操作 ‎1、画出一个三角形，使它的三个内角分别为40º，60º，80º，把你画的三角形与小组内画的进行比较，它们一定全等吗？‎ 结论：_________________________________________________________．‎ ‎2、画出一个三角形，使它的三边长分别为3cm，4cm，7cm，把你画的三角形与小组内画的进行比较，它们一定全等吗？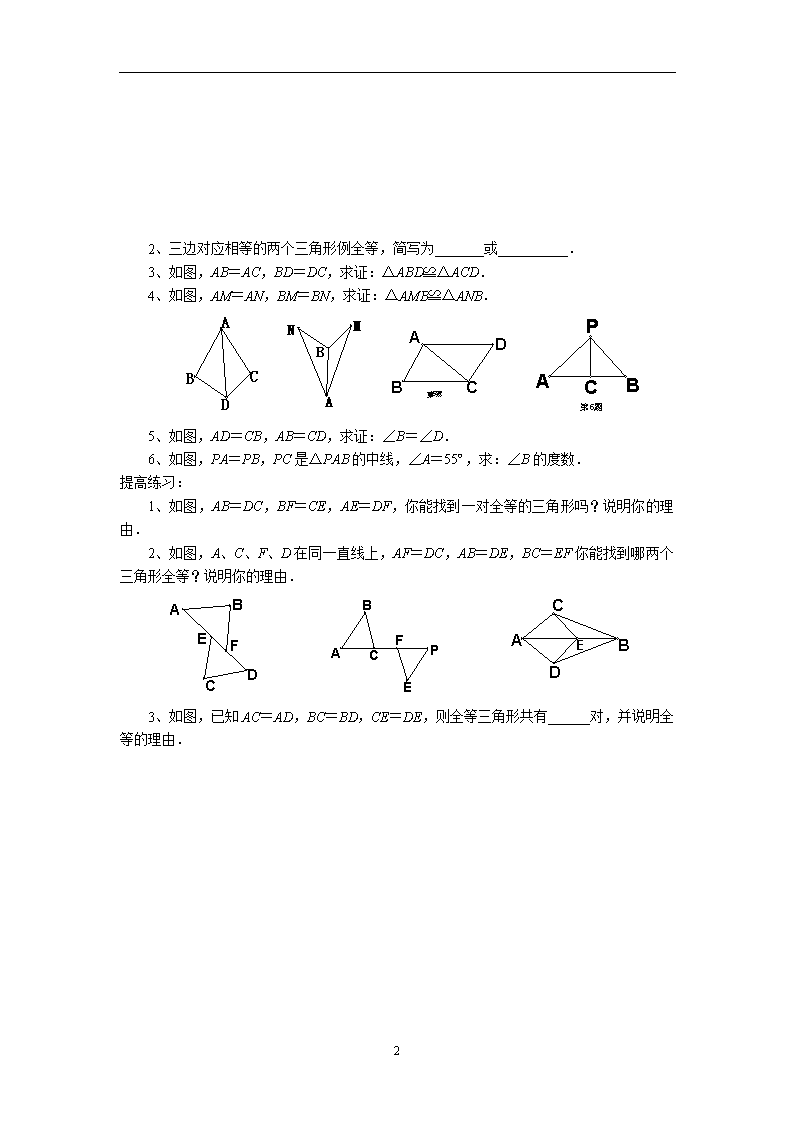‎ 结论：_________________________________________________________．‎ 二、巩固练习：‎ ‎1、下列三角形全等的是________________________________________．‎ 4‎ ‎ ‎ ‎2、三边对应相等的两个三角形例全等，简写为_______或__________．‎ ‎3、如图，AB＝AC，BD＝DC，求证：△ABD≌△ACD．‎ ‎4、如图，AM＝AN，BM＝BN，求证：△AMB≌△ANB．‎ ‎5、如图，AD＝CB，AB＝CD，求证：∠B＝∠D．‎ ‎6、如图，PA＝PB，PC是△PAB的中线，∠A＝55º，求：∠B的度数．‎ 提高练习：‎ ‎1、如图，AB＝DC，BF＝CE，AE＝DF，你能找到一对全等的三角形吗？说明你的理由．‎ ‎2、如图，A、C、F、D在同一直线上，AF＝DC，AB＝DE，BC＝EF你能找到哪两个三角形全等？说明你的理由．‎ ‎3、如图，已知AC＝AD，BC＝BD，CE＝DE，则全等三角形共有______对，并说明全等的理由．‎ 4‎ ‎ ‎ 探索三角形全等的条件（2）‎ 教学目标：‎ ‎1、经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程；‎ ‎2、掌握三角形的”角边角”“角角边”条件，了解三角形的稳定性．‎ ‎3、在探索三角形全等条件及其运用的过程中，能够进行有条理的思考并进行简单的推理．‎ 教学重点：三角形”角边角”“角角边”的全等条件 教学难点：用三角形”角边角”“角角边”的条件进行有条理的思考并进行简单的推理．‎ 教学工具：练习卷，投影仪．‎ 准备活动：‎ ‎1、三边对应相等的两个三角形全等，简写为________或_______．‎ ‎2、如图，在△ABC中，AB＝AC，AD是BC边上的中线，AD能平分∠BAC吗？你能说明理由吗？‎ ‎3、如图，‎ ‎（1）∵AC∥BD（已知），‎ ‎∴∠_____＝∠_____（___________________）．‎ ‎（2）∵AD∥BC（已知），‎ ‎∴∠_____＝∠_____（___________________）．‎ ‎4、如图3，‎ ‎∵EA⊥AD，FD⊥AD（已知），‎ ‎∴∠_________＝∠________＝90º（___________________）．‎ 教学过程：‎ 一、探索练习：‎ ‎1、如果”两角及一边”条件中的边是两角所夹的边，比如三角形的两个内角分别是60º和80º，它们所夹的边为2cm，你能画出这个三角形吗？你画的三角形与同伴画的一定全等吗？结论：___________________________________________________________．‎ ‎2、如果”两角及一边”条件中的边是其中一角的对边，比如三角形两个内角分别是60º和45º，一条边长为3cm．你画的三角形与同伴画的一定全等吗？‎ 结论：___________________________________________________________．‎ 二、巩固练习：‎ ‎1、两角和它们的夹边对应相等的两个三角形全等，简写成_______或_________．‎ ‎2、两角和其中一角的对边对应相等的两个三角形全等，简写成_______或_________．‎ ‎3、如图，AB＝AC，∠B＝∠C，你能证明△ABD≌△ACE吗？‎ ‎4、如图，已知AC与BD交于点O，AD∥BC，且AD＝BC，你能说明BO＝DO吗？‎ ‎5、如图，∠B＝∠C，AD平分∠BAC，你能证明△ABD≌△ACD？‎ 4‎ ‎ ‎ 若BD＝3cm，则CD有多长？‎ ‎6、如图，在△ABC中，BE⊥AD于E，CF⊥AD于F，且BE＝CF，那么BD与DC相等吗？你能说明理由吗？‎ 解：BD＝DC．‎ ‎7、如图，已知AB＝CD，∠B＝∠C，你能说明△ABO≌△DCO吗？‎ 三、提高练习：‎ ‎1、如图，AB∥CD，∠A＝∠D，BF＝CE，∠AEB＝110º，求∠DCF的度数．‎ ‎2、如图，在Rt△ACB中，∠C＝90º，BE是角平分线，ED⊥AB于D，‎ 且BD＝AD，试确定∠A的度数．‎ 小结：‎ 掌握三角形的”角边角”“角角边”条件，能够进行有条理的思考并进行简单的推理．‎ 作业：‎ 课本P143习题：1，2，3．‎ 教学后记：‎ 学生不能很好地掌握三角形的”角边角”“角角边”条件，对”角边角”和”角角边”容易混淆，也不能够进行有条理的思考并进行简单的推理．‎ 4‎