七年级数学下册第四章三角形2图形的全等课件（新版）北师大版 26页

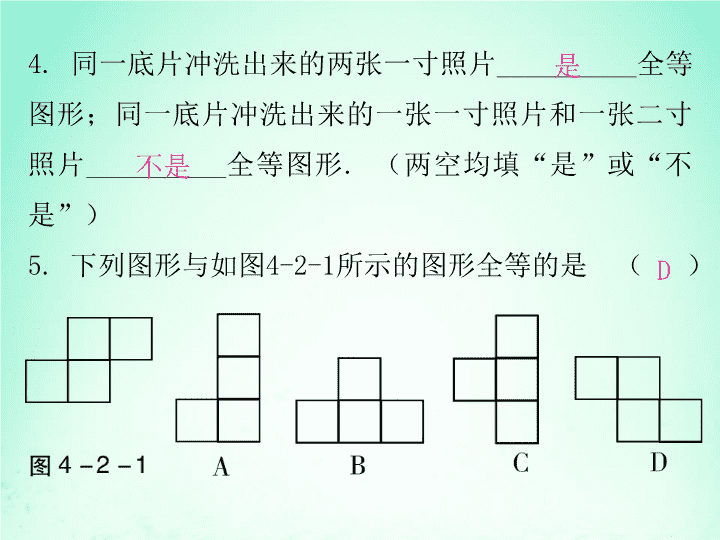
2 图形的全等 第四章 三角形 课前预习 1. 两个能够完全重合的图形称为__________，能够完 全重合的三角形称为_____________. 2. 如果两个图形全等，那么这两个图形的形状______， 大小__________. 3. 全等三角形的对应边_________，对应角_________. 记两个三角形全等时，通常把对应顶点的字母写在 __________的位置上. 全等图形 全等三角形 相同 相同 相等 相等 对应 4. 同一底片冲洗出来的两张一寸照片__________全等 图形；同一底片冲洗出来的一张一寸照片和一张二寸 照片__________全等图形. （两空均填“是”或“不 是”） 5. 下列图形与如图4-2-1所示的图形全等的是 （ 　）D 是 不是 6. 下列结论正确的是 （　） A. 形状相同的两个图形是全等图形 B. 全等图形的面积相等 C. 对应角相等的两个三角形全等 D. 两个等边三角形全等 B 课堂讲练 典型例题 新知1 全等图形的定义和性质 【例1】找出七巧板（如图4-2-2）中全等的图形. 解:由图4-2-2知：△ADE与 △CDE，△EHK与△JCF，△ADC 与△ABC，四边形AGKE与四边 形CFKE，四边形AGKD与四边形 CFKD是全等的图形. 【例2】如图4-2-4，将4×4的棋盘沿格线划分成两个 全等图形，参考图例补全另外几个. 解：如答图4-2-1所示.（答案不唯一） 模拟演练 1. 请在图4-2-3中把等边三角形分成2个、3个、4个全 等的三角形. 解：如答图4-2-2. 2. 如图4-2-5，一块土地上共有20棵果树，要把它们 平均分给四个小组去种植，并且要求每个小组分得的 果树组成的图形、形状大小要相同，应该怎样分？ 解：如答图4-2-3所示. 典型例题 新知2 全等三角形的定义及性质 【例3】如图4-2-6，△ABD是△ABC沿AB边所在直线翻折 得到的，已知∠C=100°，∠ABC=30°，则∠CAD=_____.100° 【例4】如图4-2-8，△ABC与△CDA是全等三角形，则一 定是一组对应边的是 （ ） A. AB和DC B. AC和CA C. AD和CB D. AD和DC B 模拟演练 3. 如图4-2-7，△ABC≌△CDA，并且BC=DA，那么下列 结论错误的是 （ ） A. ∠1=∠2 B. AC=CA C. AB=AD D. ∠B=∠D C 4. 如图4-2-9，点D，E在△ABC的边BC上，△ABD≌△A CE，其中B，C为对应顶点，D，E为对应顶点，下列结 论不一定成立的是 （　） A. AC=CD B. BE=CD C. ∠ADE=∠AED D. ∠BAE=∠CAD A 课后作业 夯实基础 新知1 全等图形的定义和性质 1. 下列图形中，属于全等形的是 （　）B 2. 下列四组图形中，是全等图形的一组是 （ 　）D 3. 对于两个图形，给出下列结论：①两个图形的周长 相等；②两个图形的面积相等；③两个图形的周长和面 积都相等；④两个图形的形状相同，大小也相等.其中 能获得这两个图形全等的结论共有 （ ） A. 1个 B. 2个 C. 3个 D. 4个 A 4. 在下列每组图形中，是全等形的是 （　） 5. 下列说法正确的是 （　） A. 全等三角形是指形状相同的三角形 B. 全等三角形是指面积相等的两个三角形 C. 全等三角形的周长和面积相等 D. 所有等边三角形是全等三角形 C C 新知2 全等三角形的定义及性质 6. 如图4-2-10，Rt△ABC沿直角边BC所在直线向右平移 到Rt△DEF，则下列结论中，错误的是 （　） A. BE=EC B. BC=EF C. AC=DF D. △ABC≌△DEF A 7. 下列说法正确的是 （　） A. 两个等边三角形一定全等 B. 面积相等的两个三角形全等 C. 形状相同的两个三角形全等 D. 全等三角形的面积一定相等 D 8. 如图4-2-11，△ABC≌△ADE，如果AB=5 cm， BC=7 cm，AC=6 cm，那么DE的长是 （　） A. 6 cm B. 5 cm C. 7 cm D. 无法确定 C 9. 如图4-2-12，△ABC≌△ADE，∠DAC=60°， ∠BAE=100°，BC、DE相交于点F，则∠DFB的度数是 （　） A. 15° B. 20° C. 25° D. 30° 10. △ABC全等于△DEF，用式子表示为_____________. B △ABC≌△DEF 能力提升 11. 试在图4-2-13中，沿正方形的网格线（虚线）把 这两个图形分别割成两个全等的图形. 解：如答图4-2-4所示. 12. 如图4-2-14，某校有一块正方形花坛，现要把它 分成4块全等的部分，分别种植四种不同品种的花卉， 图中给出了一种设计方案，请你再给出四种不同的设 计方案. 解：设计方案如答图4-2-5所示.