数学冀教版七年级上册教案3-3代数式的值 4页

- 1 - 3.3 代数式的值 教学目标 【知识与能力】 解代数式的值的概念，会求代数式的值，会利用求代数式的值解决较简单的实际问题. 【过程与方法】 通过游戏引入，小组充分合作探究，培养学生良好的学习习惯和规范的书写，并在游戏中发 展学生数学素养与实际应用能力. 【情感态度价值观】 在解决实际问题的过程中，初步感受两个数量之间的对应关系，进一步发展符号意识. 教学重难点 【教学重点】 （1）会求代数式的值． （2）通过求代数式的值，体会代数式是由计算程序反映的一种数量关系． 【教学难点】 通过求代数式的值，体会代数式是由计算程序反映的一种数量关系；初步感受两个数量之间 的对 应关系，进一步发展符号意识. 课前准备 无 教学过程 教学环节 教师活动 学生活动 设计意图 创设情 境，导入 新课 通过开展“扑克牌游戏”，激发学生学习的 兴趣；课前先给每一个小组发十张扑克牌， 按如下规则进行： 1、请第一位同学任意抽取一张扑克牌； 2、第二位把这个数乘以 2 传给第三位同 学； 3、第三位把听到的数加上1后传给第四位 同学； 4、4、第四位同学负责记录，并判断结果 的正误． 并规定：红色花形代表正数；黑色花形代 表负数; 大小王代表 0； 同学们了解了游戏规则，按 要求开展游戏，小组四人合 作交流完成这个游戏，并记 录相关数据。 从热身游戏入 手，激发学生们的 积极参与度，大家 在 小 组 里 面 积 极 思考，人人参与其 中，体现了高效、 以 学 生 为 主 体 的 优质课堂！ 提炼概念 用数值代替代数式中的字母，按照代数式 中给出的运算计算出的结果，叫做代数式 的值。 学生通过前面的游戏感知概 念，理解代数式就是一个计 算程序，按照给定的运算计 算出的结果就是代数式的 值。 通 过 扑 克 牌 游 戏 中 的 几 个 实 例 自 然 而 然 的 引 出 代 数式的值的定义。 学生们写出自己的书写格 式：老师进行补充和规范。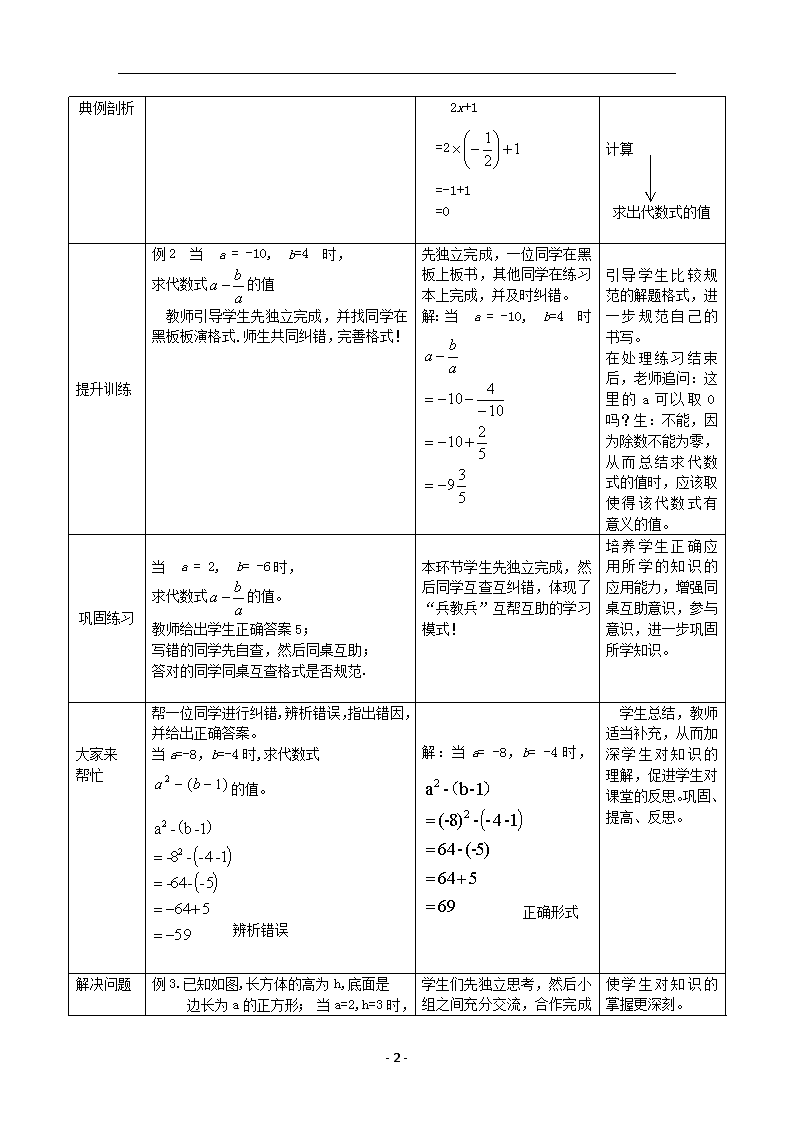 给定字母的取值 例 1.当 x= 2 1 时，求代数式 2x +1 的值。 教师走到学生身边，看学生书写过程中出 现的问题，及时给予纠正和指导。 在全班规范求代数式的值的规范书写格 式。 - 2 - 典例剖析 解：当 x= 2 1 时， 2x+1 =2 12 1      =-1+1 =0 代入代数式 计算 求出代数式的值 提升训练 例 2 当 a = -10, b=4 时， 求代数式 a ba  的值 教师引导学生先独立完成，并找同学在 黑板板演格式.师生共同纠错，完善格式！ 先独立完成，一位同学在黑 板上板书，其他同学在练习 本上完成，并及时纠错。 解：当 a = -10, b=4 时 5 39 5 210 10 410     a ba 引 导 学 生 比 较 规 范的解题格式，进 一 步 规 范 自 己 的 书写。 在 处 理 练 习 结 束 后，老师追问：这 里 的 a 可 以 取 0 吗？生：不能，因 为除数不能为零， 从 而 总 结 求 代 数 式的值时，应该取 使 得 该 代 数 式 有 意义的值。 巩固练习 当 a = 2, b= -6 时， 求代数式 a ba  的值。 教师给出学生正确答案 5； 写错的同学先自查，然后同桌互助； 答对的同学同桌互查格式是否规范. 本环节学生先独立完成，然 后同学互查互纠错，体现了 “兵教兵”互帮互助的学习 模式！ 培 养 学 生 正 确 应 用 所 学 的 知 识 的 应用能力，增强同 桌互助意识，参与 意识，进一步巩固 所学知识。 大家来 帮忙 帮一位同学进行纠错,辨析错误，指出错 因，并给出正确答案。 当 a=-8，b=-4 时,求代数式 )1(2  ba 的值。     59 564 5--64- 1-4--8- 1-b-a 2 2     ）（ 辨析错误 解：当 a= -8，b= -4 时，   69 564 )5(--64 1-4--)8-( 1-b-a 2 2     ）（ 正确形式 学生总结，教师 适当补充，从而加 深 学 生 对 知 识 的 理解，促进学生对 课 堂 的 反 思 。 巩 固、提高、反思。 - 3 - 解决问题 例 3.已知如图,长方体的高为 h,底面是 边长为 a 的正方形； 当 a=2,h=3 时， 分 别 求 出 其 体 积 V 和 表 面 积 S 。 解： ，haV 2 ，ah42aS 2  1232haV 3,2a 22   时，当 h 32248 324224aha2S 22   学生们先独立思考，然后小 组之间充分交流，合作完成 此问题。并积极思考，例 3 与前面例 1、例 2 的区别和 联系. 使 学 生 对 知 识 的 掌握更深刻。 列代数式 给定字母的取值 代入代数式 计算 求出代数式的值 殊途同归 先从两个几何图形中入手，分别列代数式 求阴影部分的面积(a+b)(a-b)和 22 ba  再延伸到任意给定 a、b 的值,计算 (a+b)(a-b)与 22 ba  的值. 你从中发现了什么规律？ 男女 PK： 给定 a、b 的取值，分别让男 女生分别求出两个代数式的 值（比如： 男生计算（a+b）（a-b）；女 生计算 22 ba  ，并请交流你 们发现的规律。 发 现 代 数 式 的 值 都相等，这也是代 数 式 的 值 的 一 个 应用。 反 思 与 小 结 学生先自己反思小结自己本节课的收获， 师生共同总结出左边的知识框架图。 代入代数式 求出代数式的值 列代数式 确定字母的取值 计算 - 4 -