七年级下数学课件：5-1-2 垂线 （共22张PPT）_人教新课标 22页

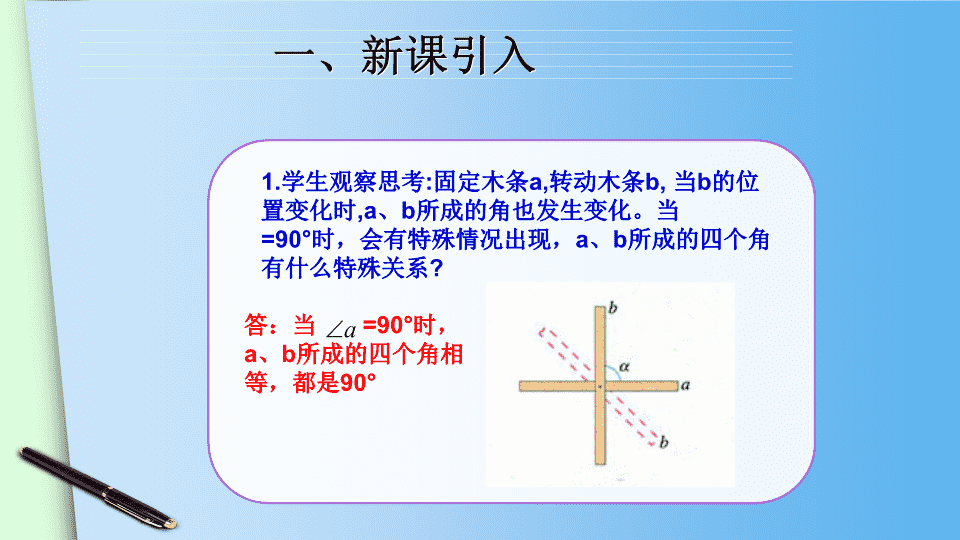
垂 线 一、新课引入 a 1.学生观察思考:固定木条a,转动木条b, 当b的位 置变化时,a、b所成的角也发生变化。当 =90°时，会有特殊情况出现，a、b所成的四个 角有什么特殊关系? 答：当 =90°时， a、b所成的四个角相 等，都是90° 1 2 3 二、学习目标 经历观察、操作、想像、归纳概括、交流等 活动,培养用几何语言准确表达的能力。 了解垂直概念,能说出垂线的性质。 会用三角尺或量角器过一点画一条 直线的垂线. 三、研读课文 垂线定义 1、两条直线相交，所成四个角中有一个角是___时， 我们称这两条直线__________，其中一条直线是 另一条直线的_____，他们的交点叫做_____。 2、垂直用符号 来表示，若“直线AB垂直于直线 CD，垂足为O”，则记为______________并在图中 任意一个角处作上直角记号。 3、用几何语言表示： 方式⑴ ∵ ∠AOC=90° ∴ AB_____CD，垂足是_____ 方式⑵ ∵ AB⊥CD于O ∴ ∠AOC=______ 知 识 点 一 C D A B O 直角 互相垂直 垂线 垂足 ⊥ AB⊥CD于O ⊥ O 90° 三、研读课文 知 识 点 一 A B C D O 练一练 1、如图所示，直线AB与CD的位置关系是垂直， 记作 ，此时，∠AOD= = = =90° AB⊥CD ∠DOB ∠BOC ∠COA 三、研读课文 知 识 点 一 2、如图所示，OA⊥OB，OC是一条射线，若 ∠AOC=120°，求∠BOC度数 解：∵ OA⊥OB ∴∠AOB=90° ∵ ∠AOC=120° ∴ ∠BOC=∠AOC﹣∠AOB =120 °﹣90°=30° 三、研读课文 知 识 点 二 一条 垂线公理 在同一平面内，过一点有且只有 直线与 已知直线垂直。 观察下图，分析探究作直线的垂线的方法，然 后作图： 三、研读课文 (2)过直线L上一点B作直线b与L垂直. 知 识 点 二 B (1)过直线L外一点A作直线a与 L垂直. A L L a b 四、归纳小结 1、两条直线相交，所成四个角中有一个角是_____时， 我们称这两条直线__________，其中一条直线是另 一条直线的________，他们的交点叫做_________。 垂直用符号____来表示 2、过一点有且只有_________直线与已知直线垂直。 3、垂线的画法：—————————————————— 4、学习反思：_______________________ ________________________ ________________________ ________________________. 直角 互相垂直 垂线 垂足 ⊥ 一条 一靠 ，二过点 ，三画线 五、强化训练 1、当两条直线相交所成的四个角都相等时，这两 条直线位置关系是 ____________________ (2) O D C B A 互相垂直 2、如图2，AO⊥BO，O为垂足，直线 CD过点O，且∠BOD=2∠AOC，则 ∠BOD=________.60° 五、强化训练 3、如图所示，直线AB⊥CD于点O，直线EF经过 点O，若∠1=26°，求∠2的度数． 解： ∵ ∠1=26°， ∠DOF= ∠1 ∴ ∠DOF=26° ∵ AB⊥CD ∴ ∠AOD=90° ∴ ∠2= ∠AOD﹣ ∠DOF =90°﹣26°=64° 五、强化训练 BP A P · . A B （2）(1) A B P· (3) 4、画一条线段或射线的垂线，就是画它们 所在直线的垂线。如图，请你过点P画出线 段AB或射线AB的垂线。 解：如图所示 垂 线（2） (1)两点之间， 最短. 一、新课引入 怎么办呢？ 线段 (2)问题:要把河中的水引到农田P处, 如何挖渠能使渠 道最短? 1 2 二、学习目标 进一步发展空间观念，用几何语言准 确表达能力。 了解垂线段的概念,了解垂线段最短的 性质,体会点到直线的距离的意义, 并 会度量点到直线的距离. 三、研读课文 知 识 点 一 垂线段及性质 1、从直线外一点引一条直线的 线，这点和 之间的 线段叫做垂线段。 ①如图，连接直线L外一点P与直线L上各点O，A1，A2， A3，…，其中 PO⊥L（我们称 为点P到直线L的垂线段）。 ②比较线段PO，PA1，PA2，PA3，…的长短， 最短。 ③结论： A2A3A4 P O B2A1 B1 垂 垂足 PO PO 连接直线外一点与直线上各点的所有线段中，垂线 段最短。 2、直线外一点到这条直线的 的 长度，叫做点到直线的距离。 垂线段 三、研读课文 知 识 点 一 练一练 1、如图所示，下列说法不正确的是（ ） A、点B到AC的垂线段是线段BC B、点A到BC的垂线段是线段AC C、线段CD是点D到线段AB的距离 D、线段BD是点B到线段CD的距离 D C B A C 三、研读课文 知 识 点 二 垂线、垂线段与点到直线的距离，是三个 不同的概念，不能混淆。 • 垂线是一条 线； • 垂线段是一条 ，是图形； • 点到直线的距离是垂线段的 ，是 一个数量，不能说垂线段是距离。 垂线、垂线段与点到直线的距离的区别 直 线段 长度 三、研读课文 知 识 点 二 练一练 1、直线AB外一点P到直线AB的距离指的是（ ） A.从P点到AB的垂线段 B.从P点到AB的垂线段的长度 C.从P点到AB的垂线 D.从P点到AB的垂线长 B 2、如右图,AC⊥BC,C为垂足,CD⊥AB,D为垂足， BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,那么 (1)点C到AB的距离是_______, (2)点A到BC的距离是________, (3)点B到CD 的距离____, D C B A 4.8 6 6.4 四、归纳小结 1、垂线段： 2、点到直线的距离： 3、连接直线外一点与直线上各点的所有线段中， 最短。简单 说成： 4、垂线、垂线段与点到直线的距离的区别是 ： 垂线是一条 线； 垂线段是一条 ，是图形； 点到直线的距离是垂线段的 ，是一个数量，不能说垂线段是距 离。 5、学习反思： 连接直线外一点与直线上各点的所有线段中，垂线 段最短。 简单说成： 垂线段最短 从直线外一点引一条直线的 垂 线，这点和 直线 之 间的线段叫做垂线段 直线外一点到这条直线的 垂线段 的长度，叫 做点到直线的距离。 垂线段 垂线段最短 直 线段 长度 五、强化训练 1、画一条线段的垂线，垂足在（ ） A、线段上 B、线段的端点 C、线段的延长线上 D、以上都有可能 2、点到直线的距离是指这点到这条直线的 （ ） A、垂线段 B、垂线的长 C、长度 D、垂线段的长 3、已知点O，画和点O的距离是3厘米的直线 可以画（ ） A、1条 B、2条 C、3条 D、无数条 A D D 五、强化训练 4、如图,在线段AB、AC、AD、AE、AF中AD最短. 小明说垂线段最短, 因此线段AD的长是点A到BF的距 离,对小明的说法,你认为________________. FEDCB A 原因：虽然线段AD是在五个线段 中，长度是最短的，但是，题意 没有说明 线段AD 是 线段BF 的 垂线段，因此，无法断定 线段AD 的长是点A到BF的距离。 小明的说法是错误的