2019七年级数学下册 第7章 平面图形的认识（二）7多边形的内角和与外角和 3页

课题：7.5　多边形的内角和与外角和（1）‎ 教学目标: ‎ ‎1．探索并了解“三角形三个内角之和等于180°”；‎ ‎2．经历举例、操作（画图、度量、拼图）、观察、归纳、说理、交流等数学活动，提升学生有条理的表达能力．‎ 教学重点：探索并掌握“三角形三个内角之和等于180°”．‎ 教学难点：理解用推理的方法说明为什么三角形的三个内角之和一定等于180°．‎ 教学方法：‎ 教学过程：‎ 一.【情境创设】‎ ‎（1）同学们，小学里我们就已经知道了三角形的三个内角的和等于多少度？‎ ‎（2）你能举例说明三角形的三个内角的和等于180°吗？‎ 二.【问题探究】 ‎ 探究一——画图、度量、计算 请每位同学在课堂笔记本上任意画一个三角形，用量角器量出各内角的度数，并求它们的和．‎ 探究二——观察 利用几何画板中的课件动画演示（通过拖动三角形的顶点改变三角形的内角），再次验证“三角形三个内角之和等于180°”．‎ 探究三——拼图 ‎（1）问：还记得小学里怎么说明“三角形三个内角之和等于180°”的吗？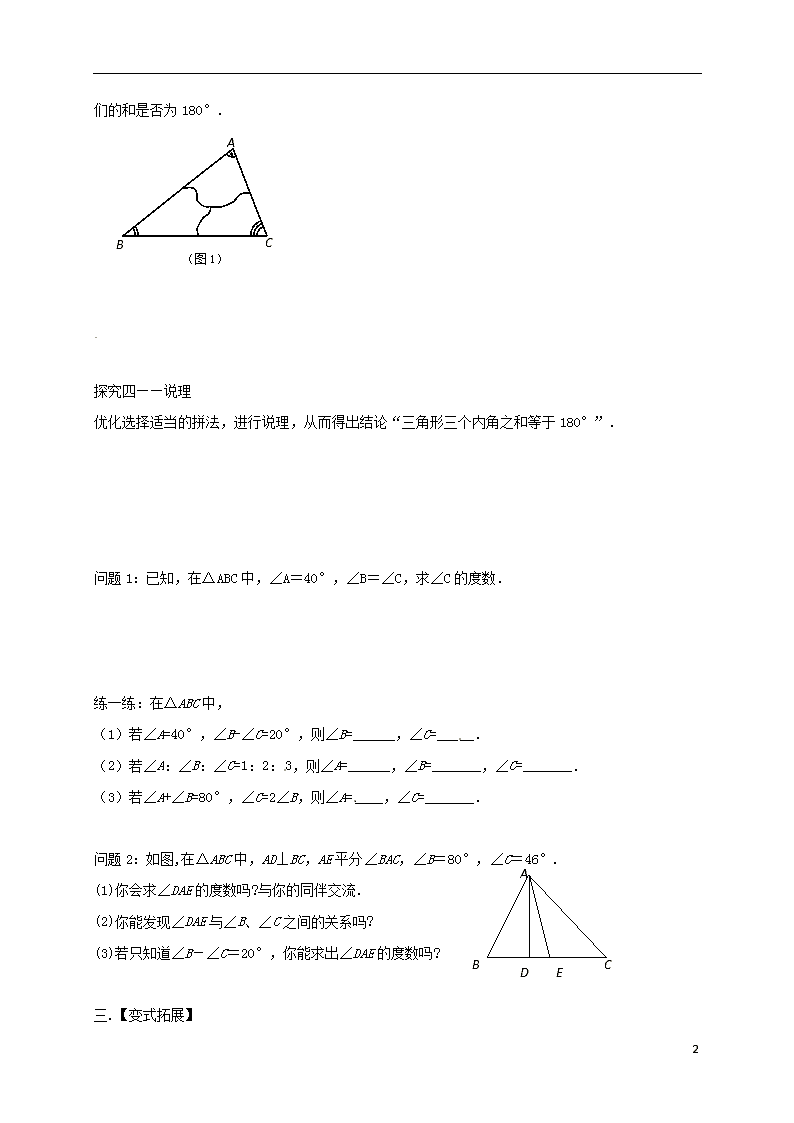‎ 3‎ ‎（2）请每位同学将课前发下的三角形纸片的3个内角（如图1）剪开，然后拼在一起，观察它们的和是否为180°．‎ A B C ‎ ‎（图1）‎ 探究四——说理 优化选择适当的拼法，进行说理，从而得出结论“三角形三个内角之和等于180°”．‎ 问题1：已知，在△ABC中，∠A＝40°，∠B＝∠C，求∠C的度数．‎ ‎ ‎ 练一练：在△ABC中，‎ ‎（1）若∠A=40°，∠B-∠C=20°，则∠B=______，∠C=_____．‎ ‎（2）若∠A：∠B：∠C=1：2：3，则∠A=______，∠B=_______，∠C=_______．‎ ‎（3）若∠A+∠B=80°，∠C=2∠B，则∠A=____，∠C=_______．‎ A B C D E 问题2：如图,在△ABC中，AD⊥BC，AE平分∠BAC，∠B＝80°，∠C＝46°.‎ ‎(1)你会求∠DAE的度数吗?与你的同伴交流.‎ ‎(2)你能发现∠DAE与∠B、∠C之间的关系吗?‎ ‎(3)若只知道∠B－∠C＝20°，你能求出∠DAE的度数吗?‎ 三.【变式拓展】‎ 3‎ 问题3：如图，ΔABC中，∠ABC与∠ACB的平分线交于点I，根据下列条件，求∠BIC的度数.‎ ‎①若∠ABC＝60°，∠ACB＝70°，则∠BIC＝＿＿＿.‎ ‎②若∠ABC＋∠ACB＝130°，则∠BIC＝＿＿＿.‎ ‎③若∠A＝50°，则∠BIC＝＿＿＿.‎ ‎④若∠A＝110°则∠BIC＝＿＿＿.‎ ‎⑤从上述计算中，我们能发现已知∠A，求∠BIC的公式是： ∠BIC＝＿＿＿.‎ ‎⑥如图，若BP，CP分别是∠ABC与∠ACB的外角平分线，交于点P，若已知∠A，则∠BPC的公式是：∠BPC＝＿＿＿.‎ 四.【总结提升】‎ 通过今天的学习，你学会了什么？你会正确运用吗？通过这节课的学习，你有什么感受呢？说出来告诉大家．‎ 3‎