八年级下数学课件《多边形的内角和与外角和》课件3_冀教版 17页

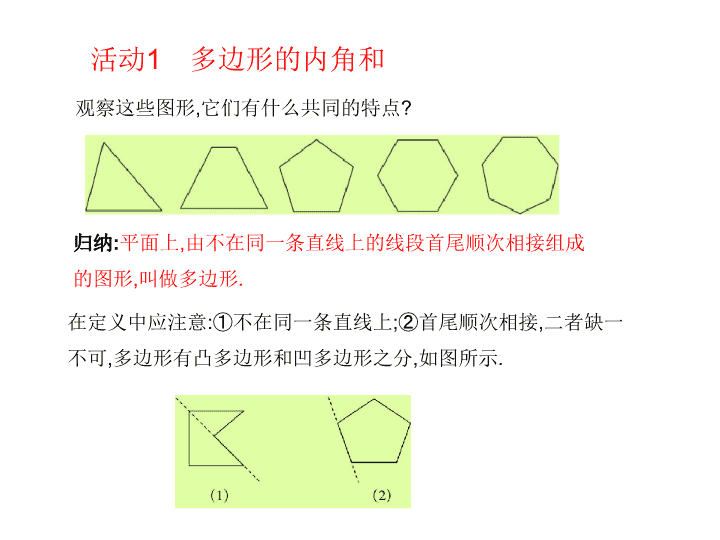
八年级数学·下 新课标[冀教] 第二十二章 四边形 学 习 新 知 问题思考 我们知道,三角形的内角和等于180°,那 么四边形的内角和等于多少度,你知道吗? 活动1　多边形的内角和 观察这些图形,它们有什么共同的特点? 归纳:平面上,由不在同一条直线上的线段首尾顺次相接组成 的图形,叫做多边形. 在定义中应注意:①不在同一条直线上;②首尾顺次相接,二者缺一不 可,多边形有凸多边形和凹多边形之分,如图所示. 多边形的边、顶点、对角线、内角、的含义 边:组成多边形的各条线段叫做多边形的边, 顶点:每相邻两条边的公共端点叫做多边形的顶点. 对角线:连接不相邻两个顶点的线段叫做多边形的对角线. 内角:多边形相邻两边组成的角叫做多边形的内角. 多边形通常以边数命名,多边形有几条边就叫做几边形.三角形、四 边形都属于多边形,其中三角形是边数最少的多边形,多边形的表示方 法与三角形、四边形类似.可以用表示它的顶点的字母来表示,既可顺 时针方向表示,也可逆时针方向表示. n边形的内角和 我们了解了多边形的有关概念后,回答下列问题: (1)一个四边形,你能设法求出它的四个内角的和吗?与同学交流. (2)还有其他的方法吗? 在求四边形的内角和时,先把四边形转化成三角形,进而求出内角 和,这种由未知转化为已知的方法是我们数学中一种非常重要的方法. 将多边形分割成不重叠的三角形,分别求四边形、五边形、六边 形的内角和,猜想n边形的内角和,并将结果填入下表. 2 3 4 1n  360 540 720 ( 2)180n  从n边形的一个顶点出发,向自身 和相邻的两个顶点无法引对角线, 向其他顶点共引(n-3)条对角线, 这时n边形被分割成(n-2)个三角 形,因为每个三角形的内角和是 180°,所以n边形的内角和为(n- 2)×180°(n≥3). 活动2　多边形的外角和 填表: 活动3　例题讲解 (教材第152页例1)已知一个多边形,它的内角和与外 角和相等,这个多边形是几边形? 解:设多边形的边数是n,那么它的内角和等于(n-2)×180°, 外角和等于360°, 由题意,得(n-2)×180°=360°. 解这个方程,得n=4. 所以,这个多边形是四边形. (教材第152页例2)如图所示,小亮从点O处出发,前进5 m 后向右转20°,再前进5 m后又向右转20°,这样走n次后 恰好回到点O处. (1)小亮走出的这个n边形的每个内角是多少度,内角和 是多少度? (2)小亮走出的这个n边形的周长是多少米? 解:(1)设这个n边形的每个内角为180°-20°=160°. 因为多边形外角和等于360°, 所以n×20°=360°.解得n=18. 所以这个n边形的内角和=(18-2)×180°=2880°. (2)5×18=90(m),所以,小亮走出的这个n边形的周长为90 m. 2.由内角和定理可以看出多边形每增加一条边,其内角和会增加180°. 4.如果多边形的每个角都相等,通常可从内角和、外角和及两者之间的 互补关系等不同角度采用不同的方法求解. 1.n边形的内角和、外角和定理是计算n边形的角的度数、边数的重要 依据.在计算中注意方程思想的应用,特别是计算边数时应用得多. 3.在利用内角和定理(n-2)×180°求边数时,先不要去括号,而把(n-2)看 作一个整体先求(n-2),再求n的值. 课堂小结 检测反馈 1.若一个多边形的内角和是1080°,则这个多边形的边数为 (　　) A.6 B.7 C.8 D.10 解析:根据n边形的内角和定理,得(n-2)×180°=1080°,解得 n=8.∴这个多边形的边数是8.故选C. C 2.若一个正多边形的一个外角是45°,则这个正多边形的边数是 (　　) A.10 B.9 C.8 D.6 解析:∵多边形的外角和是360°,∴这个正多边形的边数是 360°÷45°=8.故选C. C 3.如图所示,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边 形,则所得任意一个多边形的内角和度数不可能是 (　　) A.720°B.540° C.360° D.180° 解析:不同的划分方法有4种,如图所示.所 得任意一个多边形的内角和度数可能是 360°或540°或180°.故选A. 4.已知一个正多边形的每个外角都等于72°,则这个正多边形是 (　　) A.正五边形 B.正六边形 C.正七边形 D.正八边形 解析:正多边形的外角和是360°,且每个外角相等,因而用 360°除以外角的度数,就得到正多边形的边数.故选A. A A 5.(2016·台湾中考)如图所示的七边形ABCDEFG中,AB,DE的 延长线相交于O点.若图中∠1,∠2,∠3,∠4的外角的角度和 为220°,则∠BOD的度数为 (　　) 　A.40° B.45° C.50° D.60° 解析:延长BC交OD与点M,如图所示.∵多边形的外角和为 360°,∴∠OBC+∠MCD+∠CDM=360°- 220°=140°.∵∠OMB=∠MCD+∠MDC,∴∠BOD=180°-∠OBM- ∠OMB=180°-∠OBC-∠MCD-∠MDC=180°-140°=40°.故选A. A 6.若多边形的边数增加1,则 (　　) A.其内角和增加180° B.其内角和为360° C.其内角和不变 D.其外角和减少 解析:设原多边形的边数为n,则原多边形的内角和为(n-2)×180°,边 数增加1后的多边形的内角和为(n+1-2)×180°,∴(n+1-2)×180°-(n- 2)×180°=180°,∴其内角和的度数增加180°.故选A. A 解析:六边形的内角和为(6-2)×180°=720°,每个内角的度数为 720°÷6=120°.故选B. 7.一个六边形,每一个内角都相等,每个内角的度数为 (　　) A.100° B.120° C.135° D.150° B 解析:根据多边形的内角和定理与外角和定理列式求解. 8.一个多边形的内角和加上它的外角和等于900°,求此 多边形的边数. 解:设这个多边形的边数是n,则(n-2)×180°+360°=900°,解得n=5. 9.在各个内角都相等的多边形中,一个内角是一个外角的4倍,则这 个多边形是几边形?这个多边形的内角和是多少度? 解析:设多边形的边数为n,根据多边形的内角和定理180°×(n-2)和 多边形的外角和为360°,可得方程180°×(n-2)=360°×4,解得边 数n,再利用内角和定理即可得到内角和的度数. 解:设多边形的边数为n,180°×(n-2)=360°×4,解得n=10, 这个多边形的内角和=(10-2)×180°=1440°. 答:这个多边形是十边形,这个多边形的内角和是1440°. 10.如图所示,在四边形ABCD中,∠1=∠2,∠3=∠4,且∠D+∠C=220°, 求∠AOB的度数. 解析:首先根据四边形的内角和为360°计算出∠DAB+∠ABC=360°- 220°=140°,再根据∠1=∠2,∠3=∠4计算出∠2+∠3=70°,然后利用 三角形的内角和为180°计算出∠AOB的度数. 解:∵∠D+∠C+∠DAB+∠ABC=360°,∠D+∠C=220°, ∴∠DAB+∠ABC=360°-220°=140°. ∵∠1=∠2,∠3=∠4,∴∠2+∠3=70°, ∴∠AOB=180°-70°=110°. 11.在△ABC中,如果∠A,∠B,∠C的外角的度数 之比是4∶ 3∶ 2,求∠A的度数. 解析:因为三角形的外角和为360°,可首先求出与∠A,∠B,∠C相 邻的三个外角的度数,则可求出∠A的度数. 解:在△ABC中,设∠A,∠B,∠C的外角分别为∠1=4x,∠2=3x,∠3=2x. 因为∠1,∠2,∠3是△ABC的三个外角, 所以4x+3x+2x=360°,解得x=40°. 所以∠1=160°,∠2=120°,∠3=80°. 因为∠A+∠1=180°,所以∠A=20°. 12.如图所示,在四边形ABCD中,∠DAB的平 分线与∠ABC的平分线相交于点P.若 ∠C+∠D=220°,求∠P的度数. 解析:根据三角形的内角和等于180°,四边形的内角和等于360°,结 合角平分线的定义即可得到∠P与∠C+∠D之间的关系. 1 2 1 2 1 21 21 2 1 2 解:∵∠DAB与∠ABC的平分线交于四边形内一点P, ∴∠PAB= ∠DAB,∠PBA= ∠ABC, ∴∠P=180°-(∠PAB+∠PBA) =180°- (∠DAB+∠CBA) =180°- (360°-∠C-∠D) = (∠C+∠D). ∵∠C+∠D=220°, ∴∠P= (∠C+∠D)=110°.