浙教版八年级数学上册第一章三角形的初步认识 测试卷 11页

浙教版八年级数学上册第一章三角形的初步认识 测试卷、答案 一、选择题（每小题3分，共30分）‎ ‎1.三角形的内角和等于（    ） ‎ A. ‎90°‎                                 B. ‎180°‎                                 C. ‎270°‎                                 D. ‎‎360°‎ 解：三角形的内角和等于180度。 ‎ 故答案为：B。‎ ‎2.下列长度的三条线段，能组成三角形的是（   ） ‎ A. 3，4，8                           B. 5，6，10                           C. 5，5，11                           D. 5，6，11‎ 解：A.∵3+4＜8，故不能组成三角形，A不符合题意； ‎ B.∵5+6＞10，故能组成三角形，B符合题意；‎ C.∵5+5＜11，故不能组成三角形，C不符合题意；‎ D.∵5+6=11，故不能组成三角形，D不符合题意；‎ 故答案为：B.‎ ‎3.已知直线m∥n，将一块含45°角的直角三角板ABC按如图方式放置，其中斜边BC与直线n交于点D.若∠1=25°，则∠2的度数为（   ） ‎ ‎ ‎ A. 60°                                       B. 65°                                       C. 70°                                       D. 75°‎ 解：设直线n与AB的交点为E。 ∵∠AED是△BED的一个外角， ∴∠AED=∠B+∠1， ∵∠B=45°，∠1=25°， ∴∠AED=45°+25°=70° ∵m∥n， ∴∠2=∠AED=70°。 ‎ 故答案为：C。‎ ‎4.通过如下尺规作图，能确定点D是BC边中点的是（     ） ‎ A.                                               B.  C.                                         D. ‎ 解：A.A图所作的是BC的垂直平分线，则D是BC的中点，故A符合题意； B.B图所作的是AB的垂直平分线，则BD=AD，BD和CD不一定相等，故D不是BC的中点，故B不符合题意； C.所作的是∠BAC的角平分线，故D不一定是BC的中点，故C不符合题意； D.所作的是BC边的垂线，故D不符合题意。 故答案为：A 5.将一副直角三角板按如图所示的位置摆放，使得它们的直角边互相垂直，则 ‎∠1‎ 的度数是（   ） ‎ A. ‎95°‎                                 B. ‎100°‎                                 C. ‎105°‎                                 D. ‎‎110°‎ 解：由题意得，∠2=45°，∠4=90°-30°=60°， ∴∠3=∠2=45°， 由三角形的外角性质可知，∠1=∠3+∠4=105°。 故答案为：C 6.若长度分别为a，3，5的三条线段能组成一个三角形，则a的值可以是（   ） ‎ A. 1                                           B. 2                                           C. 3                                           D. 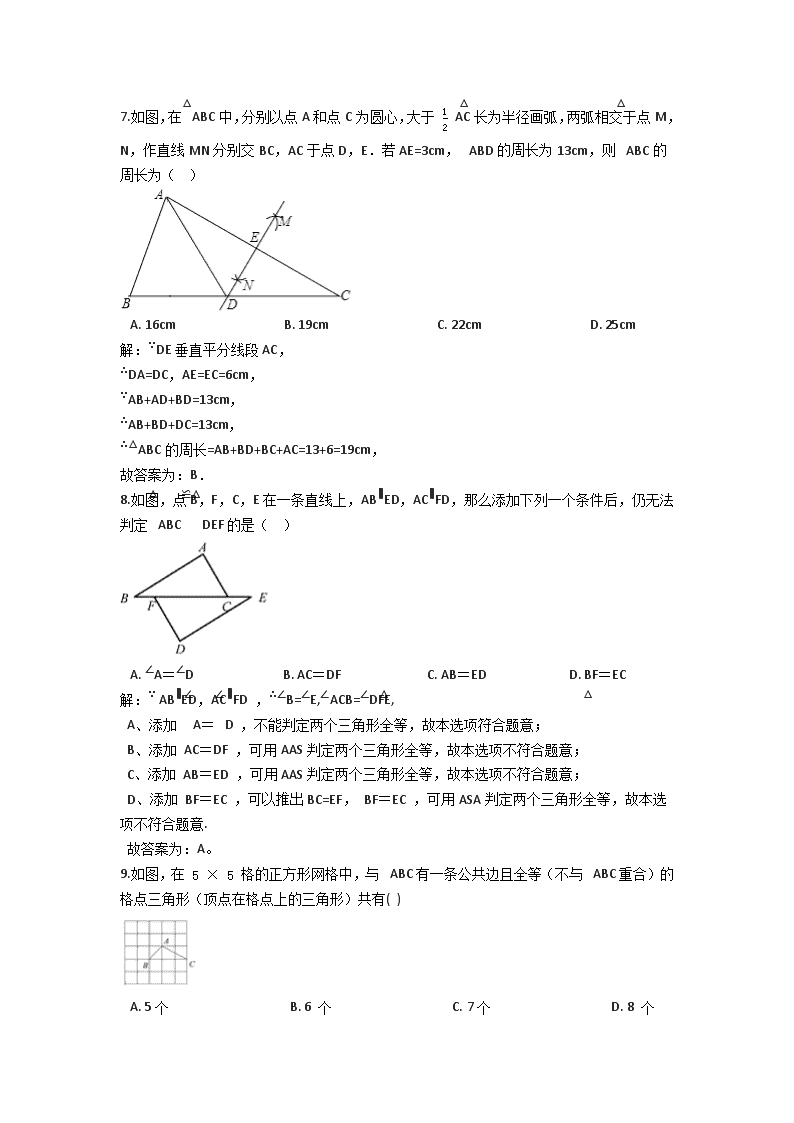8‎ 解：∵三角形三边长分别为：a，3，5， ‎ ‎∴a的取值范围为：2＜a＜8，‎ ‎∴a的所有可能取值为：3，4，5，6，7.‎ 故答案为：C.‎ ‎7.如图，在△ABC中，分别以点A和点C为圆心，大于 ‎1‎‎2‎ AC长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E．若AE=3cm，△ABD的周长为13cm，则△ABC的周长为（   ）‎ A. 16cm                                  B. 19cm                                  C. 22cm                                  D. 25cm 解：∵DE垂直平分线段AC，‎ ‎∴DA=DC，AE=EC=6cm，‎ ‎∵AB+AD+BD=13cm，‎ ‎∴AB+BD+DC=13cm，‎ ‎∴△ABC的周长=AB+BD+BC+AC=13+6=19cm，‎ 故答案为：B．‎ ‎8.如图，点B，F，C，E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（   ） ‎ A. ∠A＝∠D                            B. AC＝DF                           C. AB＝ED                          D. BF＝EC 解：∵ AB∥ED，AC∥FD ，∴∠B=∠E,∠ACB=∠DFE, A、添加 ∠A＝∠D ，不能判定两个三角形全等，故本选项符合题意； B、添加 AC＝DF ，可用AAS判定两个三角形全等，故本选项不符合题意； C、添加 AB＝ED ，可用AAS判定两个三角形全等，故本选项不符合题意； D、添加 BF＝EC ，可以推出BC=EF， BF＝EC ，可用ASA判定两个三角形全等，故本选项不符合题意. 故答案为：A。 9.如图，在 ‎5×5‎ 格的正方形网格中，与△ABC有一条公共边且全等（不与△ABC重合）的格点三角形（顶点在格点上的三角形）共有(  )‎ A. 5个                                      B. 6 个                                      C. 7个                                      D. 8 个 解：以BC为公共边可画出△BDC，△BEC，△BFC三个三角形和原三角形全等，‎ 以AB为公共边可画出三个三角形△ABG，△ABM，△ABH和原三角形全等，‎ 所以可画出6个.‎ 故答案为：B.‎ ‎10.如图，在 ‎△OAB 和 ‎△OCD 中， OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°‎ ，连接 AC,BD 交于点 M ，连接 OM ．下列结论：① AC=BD ；② ‎∠AMB=40°‎ ；③ OM 平分 ‎∠BOC ；④ MO 平分 ‎∠BMC ．其中符合题意的个数为（    ）． ‎ A. 4                                           B. 3                                           C. 2                                           D. 1‎ 解：∵ ‎∠AOB=∠COD=40°‎ ，‎ ‎∴ ‎∠AOB+∠AOD=∠COD+∠AOD ，‎ 即 ‎∠AOC=∠BOD ，‎ 在 ‎△AOC 和 ‎△BOD 中， ‎{‎OA=OB‎∠AOC=∠BODOC=OD ，‎ ‎∴ ‎△AOC≌△BOD(SAS)‎ ，‎ ‎∴ ‎∠OCA=∠ODB,AC=BD ，①符合题意；‎ ‎∴ ‎∠OAC=∠OBD ，‎ 由三角形的外角性质得： ‎‎∠AMB+∠OAC=∠AOB+∠OBD,‎ ‎∴ ‎∠AMB=∠AOB=40‎ °，②符合题意；‎ 作 OG⊥MC 于 G ， OH⊥MB 于 H ，如图所示：‎ 则 ‎∠OGC=∠OHD=90‎ °，‎ 在 ‎△OCG 和 ‎△ODH 中， ‎{‎‎∠OCA=∠ODB‎∠OGC=∠OHDOC=OD ，‎ ‎∴ ‎△OCG≌△ODH(AAS)‎ ，‎ ‎∴ OG=OH ，‎ ‎∴ MO 平分 ‎∠BMC ，④符合题意；‎ 正确的个数有3个；‎ 故答案为：B．‎ 二、填空题（每小题4分，共24分）‎ ‎11.命题“如果a+b=0，那么a，b互为相反数”的逆命题为________. ‎ 解：逆命题为：如果a，b互为相反数，那么a+b=0. ‎ 故答案为：如果a，b互为相反数，那么a+b=0.‎ ‎12.等腰三角形的两边长分别为 ‎6cm，13cm ，其周长为________cm． ‎ 解：由题意知，应分两种情况：（1）当腰长为 ‎6cm 时，三角形三边长为 ‎6，6，13，6+6<13‎ ，不能构成三角形；（2）当腰长为 ‎13cm 时，三角形三边长为 ‎6，13，13‎ ，周长 ‎＝2×13+6＝32cm．‎ ‎ 故答案为32‎ ‎ 13.如图，直线AB∥CD，OA⊥OB，若∠1＝142°，则∠2＝________度． ‎ 解：∵AB∥CD， ‎ ‎∴∠OED＝∠2，‎ ‎∵OA⊥OB，‎ ‎∴∠O＝90°，‎ ‎∵∠1＝∠OED+∠O＝142°，‎ ‎∴∠2＝∠1﹣∠O＝142°﹣90°＝52°，‎ 故答案为：52．‎ ‎14.将一副三角板如图放置，使点A落在DE上，若BC∥DE，则∠AFC的度数为________． ‎ ‎ ‎ 解：∵BC∥DE， ‎ ‎∴∠BCE=∠E=30°，‎ ‎∴∠ACF=∠ACB-∠BCE=45°-30°=15°，‎ 在Rt△ACF中，∠AFC=90°-∠ACF=90°-15°=75°．‎ 故答案为：75°．‎ ‎ 15.如图，AC=BC，请你添加一对边或一对角相等的条件，使AD=BE．你所添加的条件是________． ‎ ‎ ‎ 解：因为AC=BC, ∠C=∠C, 所以添加∠A=∠B或∠ADC=∠BEC或 ‎ CE=CD,可得△ADC与△BEC全等, 利用全等三角形的性质得出AD=BE,‎ 故答案为: ∠A=∠B或∠ADC=∠BEC或CE=CD.‎ ‎16.如图，△ABC三边的中线AD、BE、CF的公共点为G，若S△ABC=12，则图中阴影部分的面积是________． ‎ 解：∵△ABC的三条中线AD、BE，CF交于点G， ∴S△CGE=S△AGE=‎1‎‎3‎S△ACF，S△BGF=S△BGD=‎1‎‎3‎S△BCF， ∵S△ACF=S△BCF=‎1‎‎2‎S△ABC=‎1‎‎2‎×12=6， ∴S△CGE=‎1‎‎3‎S△ACF=‎1‎‎3‎×6=2，S△BGF=‎1‎‎3‎S△BCF=‎1‎‎3‎×6=2， ∴S阴影=S△CGE+S△BGF=4． 故答案为4． 三、解答题（每小题6分，共18分）‎ ‎17.如图，线段 AC 、 BD 相交于点 E , AE=DE , BE=CE .求证： ‎∠B=∠C . ‎ ‎ 证明：在△AEB和△DEC中， ‎ ‎{‎AE=DE‎∠AEB=∠DECBE=CE‎ ‎ ‎∴△AEB≌△DEC 故 ‎∠B=∠C .‎ ‎18.如图，点 E ， F 在 BC 上， BE=CF ， AB=DC ， ‎∠B=∠C ，求证： AF=DE . ‎ 证明：∵ BE=CF ， ‎ ‎∴ BE+EF=CF+EF ，即 BF=CE ，‎ 在 ΔABF 和 ΔDCE 中，‎ ‎{‎AB=DC‎∠B=∠CBF=CE‎ ，‎ ‎∴ ΔABF ≌ ΔDCE ‎(SAS)‎ ‎ ‎∴ AF=DE ‎ ‎19.已知：如图，AB=AD，BC=DC.求证：∠B=∠D. ‎ ‎ 证明：连接AC，在△ABC和△ADC中， ‎ ‎{‎AB=ADBC=DCAC=AC‎ ，‎ ‎∴△ABC≌△ADC，‎ ‎∴∠B=∠D.‎ 四．解答题（每小题8分，共48分）‎ ‎20.如图，AB＝AC，AB⊥AC，AD⊥AE，且∠ABD＝∠ACE. ‎ 求证：BD＝CE.‎ ‎ 证明：∵AB⊥AC，AD⊥AE， ‎ ‎∴∠BAE+∠CAE＝90°，∠BAE+∠BAD＝90°，‎ ‎∴∠CAE＝∠BAD.‎ 又AB＝AC，∠ABD＝∠ACE，‎ ‎∴△ABD≌△ACE(ASA).‎ ‎∴BD＝CE.‎ ‎21.如图，AB∥CD，△EFG的顶点F，G分别落在直线AB，CD上，GE交AB于点H，GE平分∠FGD．若∠EFG=90°，∠E=35°，求∠EFB的度数． ‎ 解：∵∠EFG=90°，∠E=35°， ∴∠FGH=55°， ∵GE平分∠FGD，AB∥CD， ∴∠FHG=∠HGD=∠FGH=55°， ∵∠FHG是△EFH的外角， ∴∠EFB=55°﹣35°=20°． ‎ ‎22.如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB 求证：AE=CE． ‎ 证明：∵FC∥AB， ∴∠A=∠ECF，∠ADE=∠CFE， 在△ADE和△CFE中， ‎{‎‎∠DAE=∠FCE‎∠ADE=∠CFEDE=FE ， ∴△ADE≌△CFE（AAS）， ∴AE=CE． ‎ ‎23.如图，已知：在 ΔABC 中， ‎∠BAC=‎‎90‎‎°‎ ，延长BA到点D ， 使 AD=‎1‎‎2‎AB ，点E ， F分别是边BC ， AC的中点．求证： DF=BE ． ‎ ‎ 解：∵ ‎∠BAC=‎‎90‎‎°‎ ， ‎ ‎∴ ‎∠DAF=‎‎90‎‎°‎ ，‎ ‎∵点E ， F分别是边BC ， AC的中点，‎ ‎∴ AF=FC ， BE=EC ，FE是 ΔABC 的中位线，‎ ‎∴ FE=‎1‎‎2‎AB ， FE∥AB ，‎ ‎∴ ‎∠EFC=∠BAC=‎‎90‎‎°‎ ，‎ ‎∴ ‎∠DAF=∠EFC ，‎ ‎∵ AD=‎1‎‎2‎AB ，‎ ‎∴ AD=FE ，‎ 在 ΔADF 和 ΔFEC 中， ‎{‎AD=FE‎∠DAF=∠EFCAF=FC ，‎ ‎∴ ΔADF≅ΔFEC(SAS)‎ ，‎ ‎∴ DF=EC ，‎ ‎∴ DF=BE ．‎ ‎24.如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F． ‎ ‎（1）求证：△BDE≌△CDF； ‎ ‎（2）当AD⊥BC，AE＝1，CF＝2时，求AC的长． ‎ ‎ （1）证明：∵CF∥AB， ‎ ‎∴∠B=∠FCD，∠BED=∠F.‎ ‎∵AD是BC边上的中线，‎ ‎∴BD=CD,‎ ‎∴△BDE≌△CDF.‎ ‎（2）解：∵△BDE≌△CDF，∴BE=CF=2， ‎ ‎∴AB=AE+BE=1+2=3.‎ ‎∵AD⊥BC，BD=CD，∴AC=AB=3‎ ‎25.如图①，在 ΔABC 中， AB=AC=3‎ ， ‎∠BAC=‎‎100‎‎°‎ ，D是BC的中点. ‎ 小明对图①进行了如下探究：在线段AD上任取一点P，连接PB.将线段PB绕点P按逆时针方向旋转 ‎80‎‎°‎ ，点B的对应点是点E，连接BE，得到 ΔBPE .小明发现，随着点P在线段AD上位置的变化，点E的位置也在变化，点E可能在直线AD的左侧，也可能在直线AD上，还可能在直线AD的右侧.请你帮助小明继续探究，并解答下列问题：‎ ‎（1）当点E在直线AD上时，如图②所示. ‎ ‎① ‎∠BEP=‎ ________；②连接CE，直线CE与直线AB的位置关系是________.‎ ‎（2）请在图③中画出 ΔBPE ，使点E在直线AD的右侧，连接CE.试判断直线CE与直线AB的位置关系，并说明理由. ‎ ‎（3）当点P在线段AD上运动时，求AE的最小值. ‎ ‎ （1）50 度；EC∥AB （2）解：如图③中，以P为圆心，PB为半径作⊙P. ‎ ‎∵AD垂直平分线段BC，‎ ‎∴ PB=PC ，‎ ‎∴ ‎∠BCE=‎1‎‎2‎∠BPE=‎‎40‎‎°‎ ，‎ ‎∵ ‎∠ABC=‎‎40‎‎°‎ ，‎ ‎∴ AB∥EC ‎ ‎ （3）解：如图④中，作 AH⊥CE 于H， ‎ ‎∵点E在射线CE上运动，点P在线段AD上运动，‎ ‎∴当点P运动到与点A重合时，AE的值最小，此时AE的最小值 ‎=AB=3‎ ‎