八年级下数学课件八年级下册数学课件《等腰三角形的判定与反证法》 北师大版 (6)_北师大版 24页

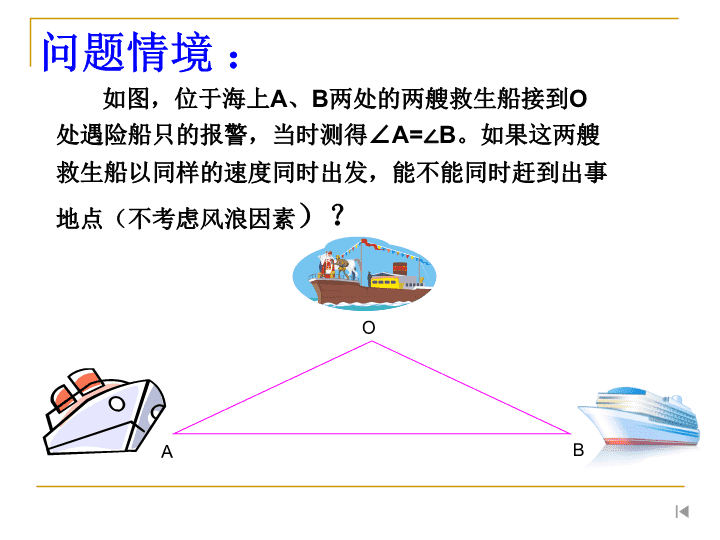
1、等腰三角形是怎样定义的？ 有两条边相等的三角形,叫做等腰三角形。 ①等腰三角形是轴对称图形。 ③等腰三角形顶角的平分线、底边上的中线、底边 上的高重合(也称为“三线合一”). ②等腰三角形的两个底角相等(简写成 “等边对等角”) 。 2、等腰三角形有哪些性质？ D A B C 既是性质又 是判定 O A B 如图，位于海上A、B两处的两艘救生船接到O 处遇险船只的报警，当时测得∠A=∠B。如果这两 艘救生船以同样的速度同时出发，能不能同时赶到 出事地点（不考虑风浪因素）？ 问题情境 ： 19.4.2 等腰三角形的判定 n学习目标： 1. 掌握等腰三角形的判定定理. 2、会综合运用等腰三角形的性质和判定进行有关的 计算和证明。 3、理解勾股定理逆定理的证明方法。 重点 难点 重点 自学课本P89---90，并完成学案----自主学习 把“等腰三角形的两个底角相等”改写成 “如果------那么-----”形式。 逆命题: 如果一个三角形有两个角相等，那么这个三角 形是等腰三角形. 如果一个三角形是等腰三角形,那么这个三角形 的两个底角相等. 它是真命题吗? 探 究 新 知 ● 操作一 做一做 你发现了什么结论？其他同学的结果与你 的相同吗？ ● 操作二 量一量，线段AB与AC的长度。 画△ABC.使∠B＝∠C＝30° AB=AC 怎样用数 学推理进 行证明呢？ A B CD 1 2 已知：如图,在ΔABC中，∠B=∠C。 求证：AB=AC 你还有其 他证法吗? 证明: 作∠BAC的平分线AD 则∠1=∠2 在△BAD和△CAD中 如果一个三角形有两个角相等,那么这两 个角所对的边也相等 ∠B=∠C ∠1=∠2 AD=AD (公共边) ∴ AB= AC (全等三角形的对应边相等) ∴ △BAD ≌ △CAD (AAS) A B C 如果一个三角形有两个角相等，那么这两 个角所对的边也相等 几何语言： ∵∠B =∠C (已知) ∴ AB=AC(等角对等边) 等腰三角形的判定定理： (简写成“等角对等边”)。 注意：在同 一个三角形 中应用哟！ 巩固练习：下列两个图形是否是等腰三角形？ 750 300 400 400 例1：如图,上午10 时，一条船从A处出发以20海里 每小时的速度向正北航行，中午12时到达B处，从A、 B望灯塔C，测得∠NAC=40°∠NBC=80°求从B处到 灯塔C的距离 解：∵∠NBC=∠A+∠C ∴∠C=80°- 40°= 40° ∴ ∠C = ∠A ∴ BA=BC（等角对等边） ∵AB=20（12-10）=40 ∴BC=40 答：B处到达灯塔C40海里 小试牛刀 80° 40° N B A C 北 大 显 身 手 如图，在△ABC中，AB=AC，∠ABC和∠ACB的平分线交 于点O.过O作EF∥BC交AB于E，交AC于F. (1)、请你写出图中所有等腰三角形，并探究EF、BE、 FC之间的关系； ∴∠2＝∠ABO ∠3＝∠ACO O A B C E F 若AB≠AC，其他 条件不变，图中 还有等腰三角形 吗？(1)中结论还 成立吗？ 解： EF=BE+CF 理由： A B C E F 1 32 4∵ EF∥BC ∴∠1＝∠2 ∠3＝∠4 ∵ BO、CO分别平分∠ABC、∠ACB ∴∠1＝∠ABO ∠4＝∠ACO ∴BE＝OE CF=OF ∵ EF=EO+FO ∴EF＝BE+CF 直角三角形的两直角边的平方和等于斜 边的平方（勾股定理 ） 如果三角形的一条边的平方等于另外两 条边的平方和，那么这个三角形是直角 三角形（勾股定理的逆定理 ） 若要证明下列定理，请你首先把它们写成 “已知…….求证…….”的形式 A B C 已知：如图， △ABC中，AC2 = AB2 + BC2 求证：△ABC是直角三角形 证明：画Rt△A’B’C’ 使∠B’=900，B’C’=BC，A’ B’=AB 由勾股定理得：A’C’2 =A’B’2 +B’C’2 = AB2 + BC2 = AC2 ∴A’C’=AC ∴ △ A’ B’C’≌ △ABC (SSS) ∴∠B=∠B’ = 900 ∴△ABC是直角三角形 A’ B’ C’ ∟ ∟ O A B 思考：如图，位于海上A、B两处的两艘救生船 接到O处遇险船只的报警，当时测得∠A=∠B。如果 这两艘救生船以同样的速度同时出发，能不能同时 赶到出事地点（不考虑风浪因素）？ 课堂小结 今天你学到了什么? 2、用构造直角三角形证明了勾股定理的逆定理。 1、等腰三角形的判定定理：等角对等边。 3、会运用等腰三角形的性质和判定进行计算和 证明。 1、如图，把一张矩形的纸沿对 角线折叠，重合部分是一个等 腰三角形吗？说明理由。 A B CD E 2、如图，AB=AC,∠A=36°BD平分 ∠ABC交AC于点D.图中有哪些等腰 三角形。选择一个说明理由。 反 馈 矫 正 3． 如图，已知P、Q是△ABC的边BC上两点，并 且BP＝PQ＝QC＝AP＝AQ，求∠BAC的大小． 解：∵PQ=AP=AQ ∴ ∠PAQ=∠APQ=∠AQ= ∠C+∠QAC= 600 ∵QC=AQ ∴ ∠C=∠QAC=300， 同理∠B=∠BAP=300 ∴ ∠BAC=∠BAP+∠PAQ+∠QAC=30+60+30=1200 小结 名 称 图 形 概 念 性质 判 定 等 腰 三 角 形 A B C 有两边 相等的 三角形 是等腰 三角形 2.等边对等角 3. 三线合一 4.是轴对称图形 2.等角对等边 1.两边相等1.两腰相等 运用等腰三角形的判定定理时， 应注意在同一个三角形中. 1、如图，∠A=36°，∠DBC=36°， ∠C=72°。分别计算∠1、∠2的度数， 并说明图中有哪些等腰三角形。 2、如图，把一张矩形的纸沿对角线 折叠，重合部分是一个等腰三角形吗？ 3、如图，AC和BD相交于点O，且 AB∥DC，OA=OB。 求证：OC=OD。 ∠1=72°，∠2=36° 等腰三角形有：△ABC，△ABD， △BCD。 A B CD E B A D C 5、已知：如图，AD ∥BC，BD平分∠ABC。 求证：AB=AD 证明：∵ AD ∥BC ∴∠ADB=∠DBC ∵ BD平分∠ABC ∴∠ABD=∠DBC ∴∠ABD=∠ADB ∴AB=AD 4、已知：如图，CD是等腰直角三 角形ABC斜边上的高，找出图中有 哪些等腰直角三角形。 等腰直角三角形有： △ABC ， △ACD ，△BCD。 A C D B 做一做：设三角形三边长分别是下列各组数，试判断 各三角形是不是直角三角形．如果是直角三角形， 请指出哪条边所对的角是直角． （1） 7， 24， 25；（2） 12， 35， 37；（3） 35， 91， 84． 根据勾股定理的逆定理可判断 （1），（2），（3）都是直 角三角形（最小两边平方和等 于最大边的平方），其中最大 边所对的角是直角。 练习 1． 说出定理“等边三角形的三个内角都相等”的 逆命题，并证明该逆命题为真命题． 逆命题：如果一个三角形的三个内角都相等，那么 这个三角形是等边三角形。证明略 2． 如图，已知P、Q是△ABC的边BC上两点，并 且BP＝PQ＝QC＝AP＝AQ，求∠BAC的大小．解：∵PQ=AP=AQ∴ ∠PAQ= ∠APQ= ∠AQP= ∠C+ ∠QAC= 60度 ∵QC=AQ∴ ∠C= ∠QAC=30度， 同理∠B= ∠BAP=30度 ∴ ∠BAC= ∠BAP+ ∠PAQ+ ∠QAC=30+60+30=120度 1. 等腰三角形的识别 1).根据等腰三角形定义； 2).等角对等边  小结 2.了解了等边三角形识别,等腰直角三角形的概念 1).三个角都是60 的三角形是等边三角形 2).顶角是直角的等腰三角形叫做等腰直角三角形 等腰三角形的性质 1.等腰三角形的两个底角相等； 2.底边上的高、中线及顶角平分线三线合一 你怎样识别一个三角形是不是等腰三角形呢？