八年级下数学课件八年级下册数学课件《线段的垂直平分线》 北师大版 (10)_北师大版 43页

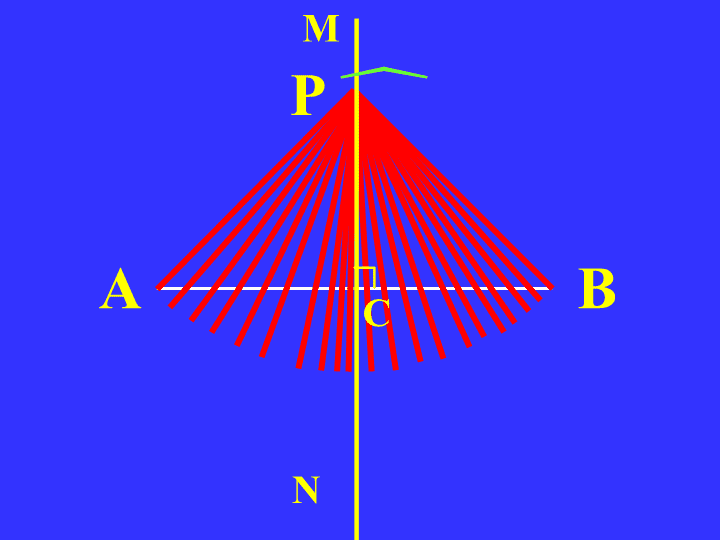
问题:如图,A、B、C三个村庄合建 一所学校,要求校址P点距离三个村 庄都相等.请你帮助确定校址.    A B C A B M N C  P M N  CA B Q A B M N P . Q. C  　　你能用不同的方法验证 这一结论吗？ 探索并证明线段垂直平分线的性质 　　如图，直线l 垂直平分线段AB，P1，P2，P3，…是 l 上的点，请猜想点P1，P2，P3，… 到点A 与点B 的距 离之间的数量关系． 　　相等． A B l P1 P2 P3 探索并证明线段垂直平分线的性质 请在图中的直线l 上任取一点，那么这一点与线段 AB 两个端点的距离相等吗？ 　　线段垂直平分线上的点与这条 线段两个端点的距离相等． A B l P1 P2 P3 线段垂直平分线上的点 和这条线段两个端点的 距离相等. 定理(线段垂直平分线的性质定理) 线段垂直平分线上的点 和这条线段两个端点的 距离相等. 定理 线段垂直平分线上的点 和这条线段两个端点的 距离相等. 定理 线段垂直平分线上的点 和这条线段两个端点的 距离相等. 定理 直线MNAB，垂足是C， 且AC=CB.点P在MN上. 已知： PA=PB求证： A BC N  M P 证明: ∵MNAB（已知） ∴PCA=PCB(垂直的定义) 在PCA和PCB中, AC=CB(已知), PCA=PCB(已证) PC=PC(公共边) ∴ PCA ≌ PCB(SAS) ∴PA=PB(全等三角形的对应边相等) A BC M N  P 线段垂直平分线上的点 和这条线段两个端点的 距离相等. 定理 8 课堂练习 　　练习1　如图，在△ABC 中，BC =8，AB 的中垂线 交BC于D，AC 的中垂线交BC 与E，则△ADE 的周长等 于______． A B C D E 解：∵　AD⊥BC，BD =DC ∴　AD 是BC 的垂直平分线 ∴　AB =AC ∵　点C 在AE 的垂直平分线上 ∴　AC =CE． ∴　AB =AC =CE 课堂练习P62 2　如图，AD⊥BC，BD =DC，点C 在AE 的垂直平 分线上，A B，A C，C E 的长度有什么关系？ AB+BD与DE 有什么关系？ A B C D E ∵　AB =CE，BD =DC，∴　AB +BD =CD +CE． 即　AB +BD =DE ． 已知线段AB,有一 点P,并且PA=PB. 那么,点P是否一定 在AB的垂直平分 线上? P A B M N   C  P / 这样的点P /不存在 探索并证明线段垂直平分线的判定 　　反过来，如果PA =PB，那么点P 是否在线段AB 的 垂直平分线上呢？ 　　点P 在线段AB 的垂直平分线上． 　　已知：如图，PA =PB． 　　求证：点P 在线段AB 的垂直平 分线上． P A B C 探索并证明线段垂直平分线的判定 证明：过点P 作线段AB 的垂线PC， 垂足为C．则∠PCA =∠PCB =90°． 在Rt△PCA 和Rt△PCB 中， ∵　PA =PB，PC =PC， ∴ Rt△PCA ≌Rt△PCB（HL）． ∴ AC =BC． 又 PC⊥AB， ∴ 点P 在线段AB 的垂直平分线上． P A B C 探索并证明线段垂直平分线的判定 　　用数学符号表示为： ∵　PA =PB， ∴　点P 在AB 的垂直平分线上． 　　与一条线段两个端点距离相 等的点，在这条线段的垂直平分 线上． P A B C 和一条线段两个端 点距离相等的点,在 这条线段的垂直平 分线上. 逆定理 小结: 1.线段的垂直平分线上的点,和这条 线段两个端点的距离相等. 2.和一条线段两个端点距离相等的 点,在这条线段的垂直平分线上. A B C          M N   C            A B M N 和线段两个端点距离相等 的所有点的集合. 线段的垂直平分线可以看作是 解：∵　AB =AC， ∴　点A 在BC 的垂直平分线． ∵　MB =MC， ∵　点M 在BC 的垂直平分线上， ∴　直线AM 是线段BC 的垂直 平分线． 课堂练习 　　练习3　如图，AB =AC，MB =MC．直线AM 是线段 BC 的垂直平分线吗？ A B C D M 例 已知:如图ABC中,边AB、BC的 垂直平分线相交于点P. 求证:PA=PB=PC. ∴ PA=PB(线段垂直平分线上的点 和这条线段两个端点距离相等) 证明: ∵ 点P在线段 AB的垂直平分线上 (已知) 同理 PB=PC ∴ PA=PB=PC. A CB M P N M/ N/ （1）为什么任意取一点K ，使点K与点C 在直线两旁？ 尺规作图 　(P62)　如何用尺规作图的方法经过直线外一点 作已知直线的垂线？ 1 2 DE（2）为什么要以大于 的长为半径作弧？ （3）为什么直线CF 就是所求作的垂线？ C A B D K F E 问题:如图,A、B、C三个村庄合建 一所学校,要求校址P点距离三个村 庄都相等.请你帮助确定校址.    A B C P  点P为校址 作图题:如图,在直线 l 上求一点P,使PA=PB l   B A P 点P为所求作的点 填空： 1.已知:如图,AD是ABC的高,E为AD上一点, 且BE=CE,则ABC为 三角形. A B C E  D 1题图 等腰 填空： 1.已知:如图,AD是ABC的高,E为AD上一点, 且BE=CE,则ABC为 三角形. 2.已知: 等腰ABC,AB=AC,AD为BC边上的高, E为AD上一点,则BE EC.(填>、<或=号) A B C E  D A B C E  D 1题图 2题图 等腰 = 3.已知:如图,AB=AC,A=30o,AB的垂 直平分线MN交AC于D,则 1= ,  2= . A B C DM N 30o 1 2 75o 30o 60o 45o 填空： 4.已知:如图,在ABC中,DE是AC的垂直平分线, AE=3cm, ABD的周长为13cm,则ABC 的周长 为 cm A B D C E  3cm 3cm 19 13cm 5.如图,CD、EF分别是AB、BC的垂直 平分线.请你指出图中相等的线段有哪些? AD =BD CF = BF AC = BC CE = BE 1 2 3 CF =DF 即:BF=CF=DF A C E B F D  证明题:1.已知:ABC中,C=90,A=30o,BD 平分ABC交AC于D. 求证:D点在AB的垂直平分线上. A BC D  证明: 30o ∵  C=90o,  A=30o(已知) ∴ ABC=60o(三角形内角和定理) ∴  A= ABD (等量代换) ∴ D点在AB的垂直平分线上.(和一 条线段两个端点距离相等的点,在这 条线段的垂直平分线上.) ∵BD平分A BC(已知) ∴ ABD=30o(角平分线的定义) 30o ∴ AD=BD(等角对等边) 证明题: 2.已知:如图,线段CD垂直平分AB,AB平分CAD. 求证:AD∥BC. A B C D O 1 2 3 证明: ∵线段CD垂直平分AB(已知) ∴ CA=CB(线段垂直平分线的 性质定理) ∴  1=  3(等边对等角) 又∵ AB平分CAD(已知) ∴  1=  2(角平分线的定义) ∴  2=  3(等量代换) ∴ AD ∥BC(内错角相等,两直线平行) 证明题:3.已知:如图,在ABC中, AB=AC,A=120o, AB的垂直平分线交AB于E,交BC于F. 求证:CF=2BF. A B C E F 300  60O300 30O CF=2AF AF=BF CF=2BF v线段垂直平分线上的点和这条线段 两个端点的距离相等. [和一条线段两个端点距离相等的点, 在这条线段的垂直平分线上. k线段的垂直平分线可以看作是和线 段两个端点距离相等的所有点的集合. 作业: P17 3. 4 证明题:4.已知:如图,AD平分BAC,EF垂直平分 AD交BC的延长线于F,连结AF. 求证:  CAF=  B. A B CD E F  123 4 A B CD E F  123 4 ∴ 1+  2= 4(等边对等角) 又∵  4= B+ 3(三角形的一个外角等于与它 不相邻的两个内角的和) ∴ 1+  2=  B+ 3 ∵ AD平分BAC(已知) ∴  2= 3(角平分线的定义) ∴ 1= B 即 CAF=  B. 证明:∵ EF垂直平分AD(已知) ∴ AF=DF(线段垂直平分线的性质定理) 如图,已知:AOB,点M、N. 求作:一点P,使点P到AOB两边的 距离相等,并且满足PM=PN. . . M NA O B . P 点P为所求 作的点