八年级上数学课件八年级上册数学课件《勾股定理的图形验证》 北师大版 (10)_北师大版 13页

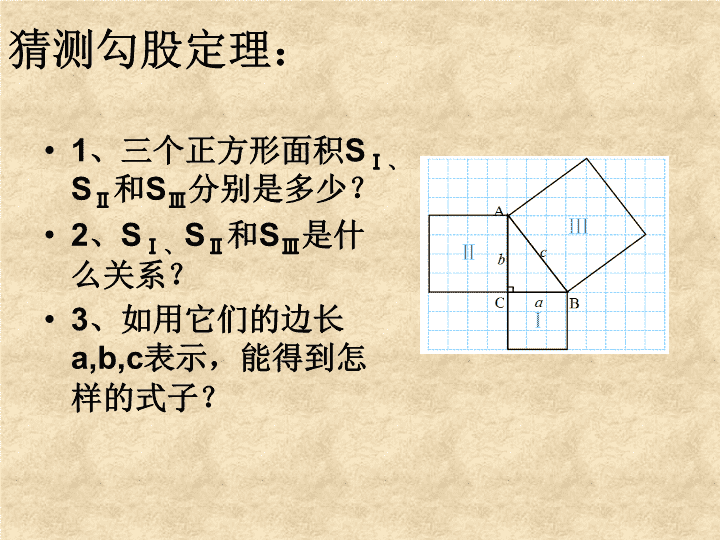
1.1 勾股定理 引入 每层楼高3米，消防队 员取来6.5米长的云如果 梯子的底部离墙基的距 离是2.5米,请问消防队 员能否进入三楼灭火? 也就是说已知直角三角形两条 直角边，会不会求第三边？ 猜测勾股定理： • 1、三个正方形面积SⅠ、 SⅡ和SⅢ分别是多少？ • 2、SⅠ、SⅡ和SⅢ是什 么关系？ • 3、如用它们的边长 a,b,c表示，能得到怎 样的式子？ • 1.割补法求三个正方形面积； • 2. SⅠ+SⅡ=SⅢ； • 3. • 勾股定理：直角三角形两条直角边的平方 和，等于斜边的平方。(短的直角边叫勾， 长的直角边叫股，斜边叫弦) 2 2 2a b c  勾股定理的背景 两千多年前，古希腊有个毕达哥拉斯 学派，他们首先发现了勾股定理，因此在 国外人们通常称勾股定理为毕达哥拉斯定 理。为了纪念毕达哥拉斯学派，1955年 希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的 国家之一。早在三千多年前，周 朝数学家商高就提出，将一根直 尺折成一个直角，如果勾等于三 ，股等于四，那么弦就等于五， 即“勾三、股四、弦五”，它被 记载于我国古代著名的数学著作 《周髀算经》中。比毕达哥拉斯 要早了五百多年。 证明勾股定理： • 已知：如图，在直角△ABC中，∠C＝90°， AB=c，BC=a, AC=b. • 求证：a2+b2=c2 方法一：将四个全等的直角三角形拼成如图 所示的正方形 2 EFGH 2 EFGH 2 2 2 2 2 =c 1=(a-b) 4 2 1 c =(a-b) 4 2 a +b =c S S ab ab       正方形 正方形 方法二：如图所示将两个直角三角形拼成直 角梯形（美国总统的证明方法） 2 21 1 1(a+b) 22 2 2ab c   2 2 2 a +b =c 梯形面积的两种 表示方式相等： 应用勾股定理： °, a b. Rt ABC C  一、在 中, 90 三边分别为a、b、c (1)已知：a=5,b=12,求c; (2)已知：a=40,c=41,求b; (3)已知：c=5,b=4,求a; (4)已知：a:b=3:4,c=15,求 、 勾股定理最直接的应用 二、已知：四边形ABCD中，∠DAB＝∠DBC＝90º AD＝3，AB＝4，BC＝12 求：DC的长。 三、已知：Rt△ABC中，AB＝４，AC＝３, 则BC的长为多少？ BC=5或 7 分类讨论的思想 课堂小结： • 通过这节课的学习，你有哪些收获？ 若a,b,c分别为直角三角形的两条 直角边和斜边，则有 222 cba  作业： • 1.课后习题1.2.3.4 • 2.查阅有关勾股定理的其它证明方法，与同 学交流讨论。