八年级下数学课件《菱形的性质与判定 2 》参考课件_鲁教版 18页

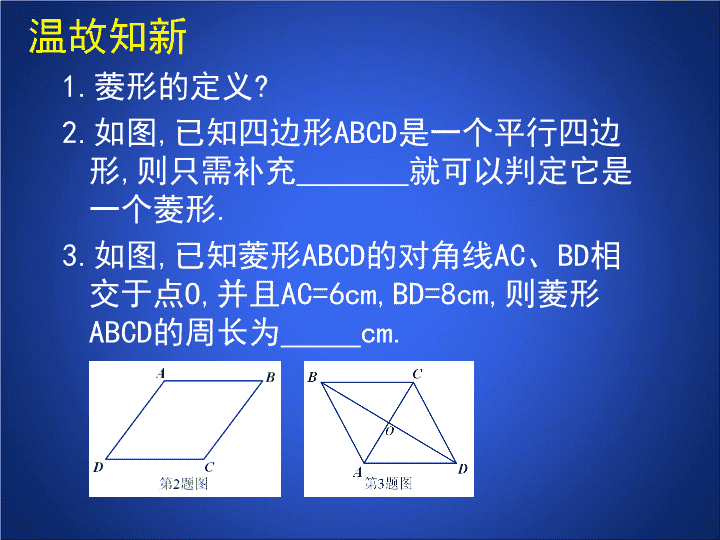
特殊平行四边形 菱形的性质与判定(二） 温故知新 1.菱形的定义? 2.如图,已知四边形ABCD是一个平行四边 形,则只需补充 就可以判定它是 一个菱形. 3.如图,已知菱形ABCD的对角线AC、BD相 交于点O,并且AC=6cm,BD=8cm,则菱形 ABCD的周长为 cm. 展示交流 上节课我们布置了几个任务: 1.在一张纸上用尺规作图做出边长为10cm的 菱形; 2.想办法用一张长方形纸剪折出一个菱形; 3.利用长方形纸你还能想到哪些制作菱形的 方法. 请向同学们展示你的作品,全班交流. 根据菱形的定义,邻边相等的平行 四边形是菱形.除此之外,你认为还有什 么条件可以判断一个平行四边形是菱形? 先想一想,再与同伴交流. 探索新知 平行四边形的不少性质定理与判定 定理都是互逆命题.受此启发,我猜想: 四边相等的四边形是菱形,对角线垂直 的平行四边形是菱形. 小明的想法 我觉得,对角线互相垂直的平行四 边形有可能是菱形.但“四边相等的平 行四边形是菱形”嘛……实际上与“邻 边相等的平行四边形是菱形”一样. 小颖的想法 你是怎么想的?你认为小明的想法 如何?与同伴交流一下. 对角线互相垂直的平行四边形是菱形吗? 试一试 已知:如图1-3,在□ABCD中,对角线AC与 BD交于点O,AC⊥BD. 求证: □ABCD是菱形 证明:∵四边形ABCD是平行四边形 ∴OA=OC 又∵AC⊥BD ∴BD是线段AC的垂直平分线 ∴BA=BC ∴四边形ABCD是菱形(菱形定义) 定理 对角线互相垂直的平行四边形是菱形 ∵四边形ABCD是平行四边形 又∵AC⊥BD ∴四边形ABCD是菱形 ( ) 议一议 已知线段AC,你能用尺规作图的方法做一 个菱形ABCD,使AC为菱形的一条对角线吗? A C 议一议 以下是小刚的作法 你是怎么做的?你认为小刚的作法正确吗?与 同伴交流. 请尝试证明下面的定理 已知:如图1-5,四边形ABCD中,AB=BC=CD=DA. 求证: 四边形ABCD是菱形 证明:∵AB=CD,AD=BC ∴四边形ABCD是平行四边形 又∵AB=BC ∴四边形ABCD是菱形(菱形定义) 四条边相等的四边形是菱形 定理 四条边相等的四边形是菱形 ∵AB=BC=CD=DA ∴四边形ABCD是菱形 ( ) 做一做 你能用折纸等办法得到一个菱形吗?动手试一试. 先将一张长方形的纸对折,再对折,然后沿图中 的虚线剪下,将纸展开,就得到了一个菱形. 你能说说这样做的道理吗? 证明:在△AOB中, ∴AB2=OA2+OB2 ∴△AOB是直角三角形,∠AOB是直角. ∴AC⊥BD ∴□ABCD是菱形 (对角线垂直的平行四边形是菱形) ∵ AB= √5,OA=2,OB=1 运用巩固 1.课本P7随堂练习 2.课本P8习题1.2 知识技能 1 课堂小结 1.本节课重点学习了什么知识,应用了哪 些数学方法？ 2.判定一个四边形是菱形有哪些方法? 3.通过本节课的学习你有哪些收获？在 今后的学习过程中应该怎么做？ 布置作业 1.课本P8 知识技能 2 数学理解 3 2.预习课本P8-9内容