- 411.07 KB
- 2021-11-01 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
线段的垂直平分线(2)
一 回顾与思考
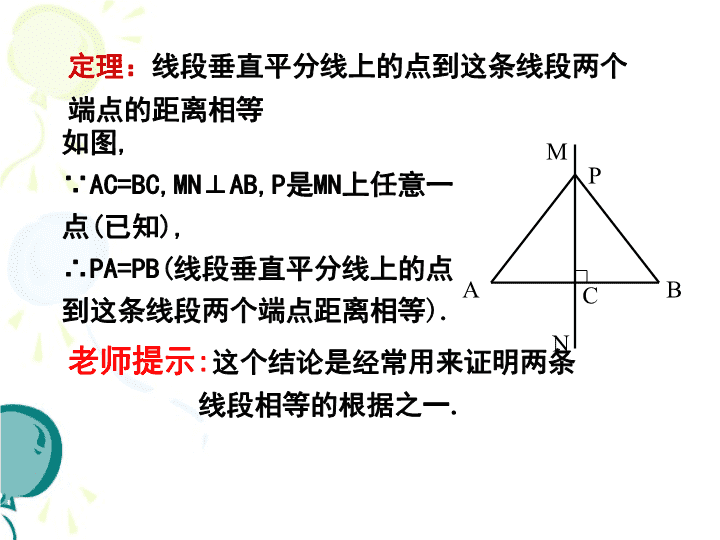
定理:线段垂直平分线上的点到这条线段两个
端点的距离相等
老师提示:这个结论是经常用来证明两条
线段相等的根据之一.
N
A C B
P
M如图,
∵AC=BC,MN⊥AB,P是MN上任意一
点(已知),
∴PA=PB(线段垂直平分线上的点
到这条线段两个端点距离相等).
逆定理 到一条线段两个端点距离相等的点,在这
条线段的垂直平分线上.
几何语言描述:
如图,
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段
两个端点距离相等的点,在这条线段的
垂直平分线上).
老师提示:这个结论是经常用来证明点在直线
上(或直线经过某一点)的根据之一.
A B
P
已知:线段AB,(如图).
求作:线段AB的垂直平分线.
作法:
回顾思考:
用尺规作线段的垂直平分线.
1.分别以点A和B为圆心,以大AB/2
长为半径作弧,两弧交于点C和D.
A B
C
D
2. 作直线CD.
则直线CD就是线段AB的垂直平分线.
想一想:请你说明CD为什么是AB的
垂直平分线,并与同伴进行交流.
特别提示:
因为直线CD与线段AB的交点就是AB的
中点,所以以后我们经常也会用这种方法
作线段的中点.
二 学习新知
剪一个三角形纸片通过折叠找出每条
边的垂直平分线.
观察这三条垂直平分线,你发现了什么?
结论:三角形三条边的垂直平分线
相交于一点.
你想证明这个命题吗?
你能证明这个命题吗?
老师期望:
你能写出规范的证明过程.
利用尺规作出三角形三条边的垂直平分线.
再观察这三条垂直平分线,你又发现了什么?
与同伴交流.
结论:三角形三条边的垂直平分线相交
于一点.
你想证明这个命题吗?
你能证明这个命题吗?
老师期望:
你能写出规范的证明过程.
如何证三条直线交于一点?
命题:三角形三条边的垂直平分线相
交于一点.
基本想法是这样的:我们知道,两条直
线相交只有一个交点。要想证明三条直线
相交于一点只要能证明两条直线的交点在
第三条直线上即可.这时可以考虑前面刚
刚学到的逆定理.
如图,在△ABC中,设AB,BC的垂直平分线相交
于点P,连接AP,BP,CP.
∵点P在线段AB的垂直平分线上,
∴PA=PB .
同理,PB=PC.
∴PA=PC.
∴点P在线段AC的垂直平分线上,
∴AB,BC,AC的垂直平分线相交于一
点.
A
B C
P
定理:三角形三条边的垂直平分线相交于
一点,并且这一点到三个顶点的距离相等.
想一想:仿照我们上节课讲的线段垂直
平分线的定理以及逆定理的几何语言的表
示方法,你能把这个定理也用几何语言表
示出来吗?
试一试:你能独立完成这个写作过程吗?
老师提示:这是证明三条直线交于一点的根据.
如图,在△ABC中,
∵c,a,b分别是AB,BC,AC的垂直平分线(已知),
∴c,a,b相交于一点P,且PA=PB=PC(三角形三条
边的垂直平分线相交于一点,并且这一点到三个
顶点的距离相等). A
B C
P
a
bc
三 挑战自我
(1)已知三角形的一条边及这条边上的高,
你能作出三角形吗?
如果能,能作出几个?所作出的三角形都全等
吗?
老师期望:你能亲自探索出结果并能用尺规
作出图形.
(2)已知等腰三角形的底及底边上的高,你能
用尺规作出等腰三角形吗?能作几个?
例题
已知底边及底边上的高,利用尺规作等腰三角形.
已知:线段a,h(如图).
a h
求作: △ABC,使AB=AC,且BC=a,高AD=h.
老师期望:你能独立写出作法.
请你写出作法.
作法:
(1)作线段BC=a(如图)
(2)作线段BC的垂直平分线m,
交BC于点D
(3)在m上作线段DA,使DA=h
(4)连接AB,AC
△ABC为所求的等腰三角形
h
a
B C
A
D
m
已知直线 l 和 l 上一点P,利用尺规作l的垂线,使它经过
点P.
已知:直线l和l上一点P.
求作:PC⊥ l .
作法:1、以点P为圆心,以任意长为半
径作弧,与直线l 相交于点A和B.
2.作线段AB的垂直平分线PC.
直线PC就是所求的垂线.
lP
A B
C
做一做
四 学以致用
1.已知线段a,求作以a为底,以a/2为高的
等腰三角形.这个等腰三角形有什么特征?
老师提示:先分析,作出示意图形,再按要
求去作图.
2.如图,已知△ABC,求作:
(1)AC边上的高;(2)BC边上的高. A
B C
老师提示:钝角三角形中三边的高的情况.
3.为筹办一个大型运动会,某市政府打算修建一
个大型体育中心.在选址过程中,有人建议该体育
中心所在位置应当与该城市的三个城镇中心(如
图中P,Q,R表示)的距离相等.
老师期望:养成用数学解释生活的习惯.
P●
Q● R●
P●
Q●
R●(1) (2)
(1).根据上述建议,试在图(1)中画出体育中心
G的位置;
(2).如果这三个城镇的位置如图(2)所示,∠RPQ
是一个钝角,那么根据上述建议,体育中心G应在
什么位置?
(3).你对上述建议有何评论?你对选址有什么建议?
P●
Q● R●
P●
Q●
R●(1) (2)
4,如图,某市三个城镇中心A,B,C恰好分别位于
一个等边三角形的三个顶点处,在三个城镇中心
之间铺设通信光缆,以城镇A为出发点设计了三
种连接方案:
(1)AB+BC
(2)AD+BC(D为BC的中点)
(3)OA+OB+OC(O 为△ABC三边的垂直平分线的交点)
要使铺设的光缆长度最短应选哪种方案?
A
B C
A
DB C
O
D CB
A
(1)AB+BC
(2)AD+BC(D为BC的中点)
(3)OA+OB+OC(O为△ABC三边的垂直平分线)
五 回顾与小结
定理 三角形三条边的垂直平
分线相交于一点,并且这一
点到三个顶点的距离相等.
如图,在△ABC中,
∵c,a,b分别是AB,BC,AC的垂
直平分线(已知),
∴c,a,b相交于一点P,且
PA=PB=PC(三角形三条边的
垂直平分线相交于一点,并
且这一点到三个顶点的距
离相等).
A
B C
P
a
bc
尺规作图的解题格式(六步骤):
已知: 作法:
求作: 证明:
分析: 讨论:
课外作业
P34 复习题8、9题.
祝你成功!
结束寄语
严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相
应,言必有据.这是初学证明者谨记和遵
循的原则.
相关文档
- 八年级下数学课件《二次根式的加减2021-11-0117页
- 八年级下数学课件伟达定理 刘明友_2021-11-0112页
- 八年级下数学课件八年级下册数学课2021-11-0119页
- 八年级下数学课件《用配方法解一元2021-11-0115页
- 八年级下数学课件《一次函数的应用2021-11-0118页
- 八年级下数学课件:第十七章 勾股定2021-11-0125页
- 八年级下数学课件八年级下册数学课2021-11-0110页
- 八年级下数学课件《确定事件与随机2021-11-0122页
- 八年级下数学课件:18-1-1 平行四边2021-11-0125页
- 八年级下数学课件:18-2-3 正方形 (2021-11-0123页