八年级下数学课件《三角形的中位线》 (8)_苏科版 15页

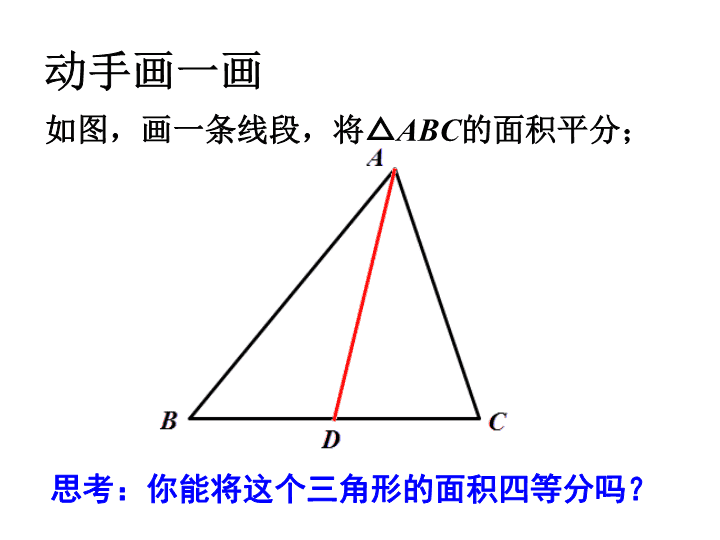
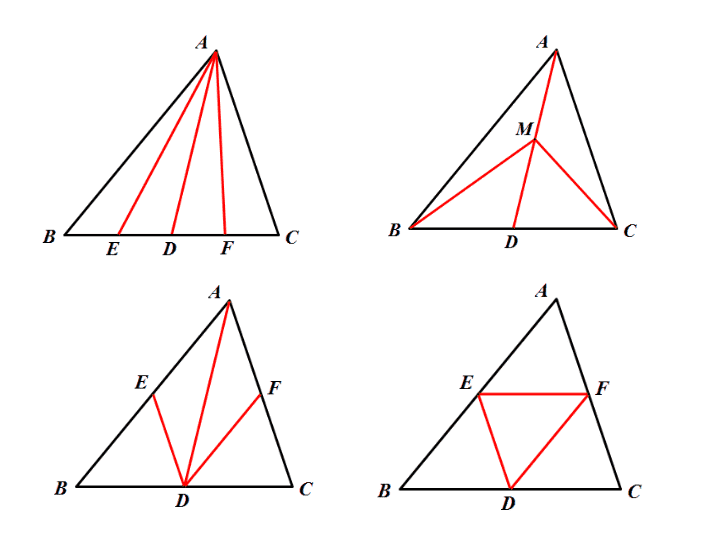
情景引入 三角形中三条重要的线段分别是什么？ 中线、高、角平分线 动手画一画 如图，画一条线段，将△ABC的面积平分； 思考：你能将这个三角形的面积四等分吗？ 观 察： 图中，点D、E、F的 位置有什么特征？ 9.5 三角形的中位线 连接三角形两边中点的线段叫做三角 形的中位线. 三角形有几 条中位线？三角形中位线定义： 如图：∵E、F是AB、AC中点 ∴EF是△ABC的中位线 想一想： 三角形的中线与三角形的中位线有什么区别？ 中线是一个顶点和对边中点的连线 中位线是两边中点的连线 思考： 如图，EF是△ABC的中位线，那么EF 具有什么性质呢？ 根据旋转可知： EF=FH,AE=CH，∠A= ∠HCF ∴EF= EH, AB//CH 即BE//CH ∵E是AB中点 ∴AE=BE ∴BE=CH ∴四边形BCHE是平行四边形 ∴EH//BC，EH=BC 即EF//BC，EF= BC 2 1 2 1 数学化认识 ∵E、F是AB、AC的中点， ∴EF∥BC，EF＝ BC 三角形中位线定理： 三角形的中位线平行于第三边， 并且等于第三边的一半． 符号语言： 2 1 如图，已知D、E分别为AC和AB 的中点， DE＝5，求BC的长； 基础练习 变式1：如图，若F为 BC的中点，且AC＝ 8，∠C＝70°，求 EF的长和∠DEF的 度数； 变式2：连接DF，若 △DEF的周长为 12cm，求△ABC的 周长；如果连接AF， 那么AF与DE有什么 关系？ 为什么？ 3 连接CE，若 ∠ACB=90° 求证： CE=DF . 例： 如图，在四边形ABCD中，E、F、G、 H分别是四边中点，则四边形EFGH是平行 四边形吗？为什么？ 例题讲解 A B F C G D E H 变1：如果四边形 ABCD中，对角线 AC=BD，那么四边 形EFGH会不会是 特殊的平行四边形？ 为什么？ 例： 如图，在四边形ABCD中，E、F、G、 H分别是四边中点，则四边形EFGH是平行 四边形吗？为什么？ 例题讲解 A B F C G D E H 变2：如果四边形 ABCD中，对角线 AC⊥BD，那么四 边形EFGH会不会 是特殊的平行四边 形？为什么？ 三角形的中位线有什么性质? 课堂小结 三角形中位线定理，是我们证 明两直线平行和线段之间数量关系 的一种重要途径。 课堂反馈 书P87 练习1，2 如图，在平行四边形ABCD中，E、F分别 是BC、AD的中点，AE与BF相交于点G， DE与CF相交于点H，试说明GH∥AD且 GH= AD. 2 1 G H E F D A B C 拓展延伸