八年级下数学课件：17-1 勾股定理 （共18张PPT）1_人教新课标 18页

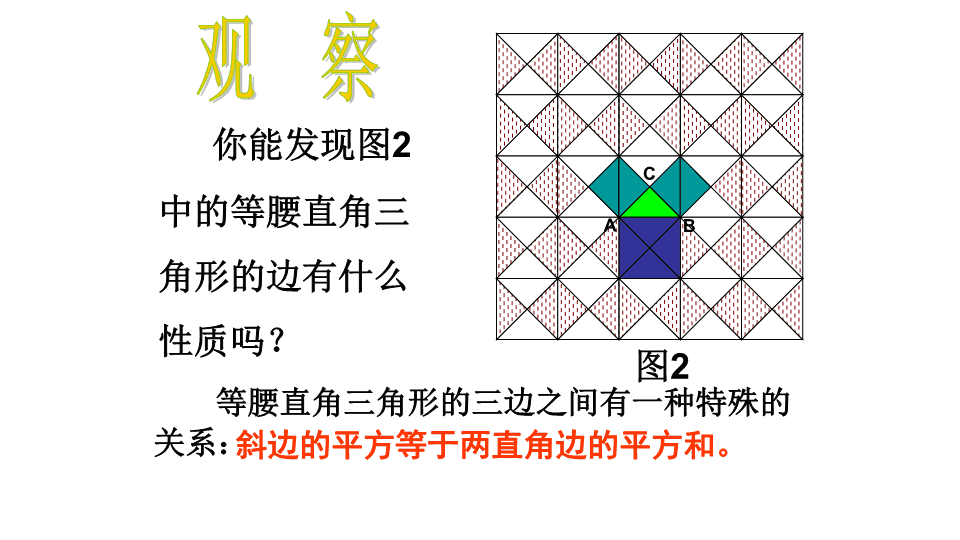
勾股定理 d a b c 问题：要修一个育苗 棚，棚宽a＝4m，高 b＝3m，长d＝10m， 求：覆盖在顶上的塑 料薄膜需多少m2? 等腰直角三角形的三边之间有一种特殊的 关系： 　　你能发现图2 中的等腰直角三 角形的边有什么 性质吗？ 图2 A B C 斜边的平方等于两直角边的平方和。 　　 等腰直角三角形 有上述性质，其他的 直角三角形也有这个 性质吗？图3中每个小 方格的面积均为1，分 别算出图中正方形A、 B、C的面积，看看能 得出什么结论。 B A C 图3 由上面的几个例子，我 们猜想： 命题1　如果直角三角形 的两直角边长分别为a，b， 斜边长为c，那么a2+b2=c2。 思考：这个猜想是普遍规律吗？ 1、拼成的图形中有___个正方形，有 ___个直角三角形 2、图中大正方形的边长为___，小正 方形的边长是______ 3、图中大正方形面积为___，小正方 形的面积为______，四个直角三角形面积为 ______从图中可以看到大正方形面积等于小 正方形面积与四个直角三角形面积之和，于是可列等 式为__________________，化简整理可得_______ 图4 c a b 2 4 C a-b C2 (a-b)2 1 2 ab×4 C2= (a-b)2 + 1 2 ab×4 a2+b2=c2 c a b 图3 2 1 c a b 1 2 图2 1、图1的面积是：a2+b2 2、将图1中三角形1和2移动到 图2的位置，就会形成一个以C 为边长的正方形如图3。由此得 到：图1的面积等于图3的面积. 即：a2+b2=c2 a b c 图1 1 2 　　在国外，相传勾股定理是公元前 500多年前古希腊数学家毕达哥拉斯首 先发现的，因此又称此定理为“毕拉哥 拉斯定理”法国和比利时称它为“驴桥 定理”，埃及称它为“埃及三角形”等， 但它们发现的时间都比我国要迟得多。 勾股定理的命名 经过证明被确认正确的命题叫做定 理。我国把命题1称为“勾股定理”而 西方叫“毕拉哥拉斯定理”。 例1：在Rt△ABC中， ∠ C=900 ∠A、∠B、∠C所对边分别为a、b、 c。已知a=5，b=12， 求c。 例2：在Rt△ ABC中，∠ B=900， ∠ A、∠ B、∠ C，所对边分别为a、 b、c已知a=40，b=41，求c。 d a b c 问题：要修一个育苗 棚，棚宽a＝4m，高 b＝3m，长d＝10m， 求：覆盖在顶上的塑 料薄膜需多少m2? 现在让我们大家一起来解答刚才引入的问题。 d a b c 答：覆盖在顶上的塑料面积 要50m2 。　 解：由勾股定理得：a2+b2=c2 因为a=3,b=4 所以c2=32+42=25,即 c=5 所以s长方形＝cd=5X10=50 探究1: 一个门框的尺寸如图所 示，一块长3m，宽2.2m的 薄木板能否从门框内通过？ 为什么？ 1m 2m B A C 解：在Rt △ABC中，根据勾股定理： AC2=AB2+BC2 =12+22=5 因此，AC= 5 ≈2.236 因为AC （大于、小于、等于） 木板的宽，所以木板 （能、不 能）从门框内通过。 探 究二: 如图：一个3m长的梯子AB，斜靠在一竖直的墙 AO上，这时AO的距离为2.5m，如果梯子的顶端A沿 墙下滑0.5m，那么梯子底端B也外移0.5m吗？ A DB C 2.5m ？ 0.5m 可以看到，BD=OD-OB，求BD，可以 先求OB，OD。在Rt△AOB中， OB2=______________OB=________ 在Rt△COD中 OD2=_________________________ OD =__________________________ BD =__________________________ 梯子的顶端沿墙下滑0.5m，梯子底端外 移_______m。O AB2-AO2 0.58 CD2-CO2 2.24 1.66 0.58 1、有一个边长为50dm的正方形洞口，想用 一个盖去盖住这个洞口，圆的直径至少多长(结果 保留整数)。 2、如图，池塘边有两点A、B，点C是与BA 方向成直角的AC方向上一点，测得CB=60m， AC=20m，你能求出A、B两点间的距离吗(结果保 留整数)？ 练习： A C B 20m 60m 1、在直角三角形ABC中，C=900， 若 a=9，b=40则c=____ 2、若角三角形三边长为三个连续偶 数，则它的三边长分别为（　） A、2、4、6 B、4、6、8 C、6、8、10 D、8、10、12 C 41 2、利用勾股定理进行有关计 算和证明时，应注意哪些 问题？ 1、通过这节课你学到了哪些 　 知识？ 作业:教科书 第78页习题18.1第二题; 第三题;第七题