【精品试题】人教版 八年级下册数学 第十八章 平行四边形周周测9（全章）（含答案） 11页

第 1 页 共 11 页 第十八章 平行四边形周周测 9 一 选择题 1.下 列 命 题 中 ,真 命 题 是 （ ） A． 对 角 线 相 等 的 四 边 形 是 矩 形 B.对 角 线 互 相 垂 直 的 四 边 形 是 菱 形 C.对 角 线 互 相 平 分 的 四 边 形 是 平 行 四 边 形 D.对角线互相垂直平分的四边形是正方形 2.下列命题中，不正确的是（ ） A．有一个角是 60°的等腰三角形是等边三角形 B.一组对边平行且一组对角相等的四边形是平行四边形 C.对角线互相垂直且相等的四边形是矩形 D.对角线相等的菱形是正方形 3.已知▱ ABCD 的周长为 32，AB=4，则 BC=（ ） A．4 B．12 C．24 D．28 4.如图,在平行四边形 ABCD 中,∠BAD 的平分线交 BC 于点 E,∠ABC 的平分线交 AD 于点 F, 若 BF=12,AB=10,则 AE 的长为（ ） A．13 B．14 C．15 D．16 5.如图,将▱ ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连 接BE.若BE平分∠ABC,且AB=5,BE=4,则AE=（ ） A．2 B．3 C．4 D．5 6.如图，在菱形 ABCD 中，BE⊥AD，BF⊥CD，E、F 为垂足，AE=ED ，则∠EBF 等于( ) A．75° B．60° C．50° D．45° 第 2 页 共 11 页 7.如图,在△ABC中,AB=5，BC=6,AC=7,点D,E,F分别是△ABC三边的中点，则△DEF周长为 （ ） A．9 B．10 C．11 D．12 8.如图,在菱形 ABCD 中,AB=5,对角线 AC=6.若过点 A 作 AE⊥BC,垂足为 E,则 AE 的长为 ( ) A．4 B．2.4 C．4.8 D．5 9.某校的校园内有一个由两个相同的正六边形(边长为 2.5m)围成的花坛，如图中的阴影部分 所示，校方先要将这个花坛在原有的基础上扩建成一个菱形区域如图所示，并在新扩充的部 分种上草坪，则扩建后菱形区域的周长为( ) A．20m B．25m C．30m D．35m 10.如图,菱形 ABCD 中,∠B=60°,AB=4,则以 AC 为边的正方形 ACEF 的周长为( ) A．14 B．15 C．16 D．17 11.如图，菱形 ABCD 的对角线相交于坐标原点，点 A 的坐标为(a，2)，点 B 的坐标为(﹣1， ﹣ )，点 C 的坐标为(2 ，c)，那么 a，c 的值分别是( ) 第 3 页 共 11 页 A．a=﹣1，c=﹣ B．a=﹣2 ，c=﹣2 C．a=1，c= D．a=2 ，c=2 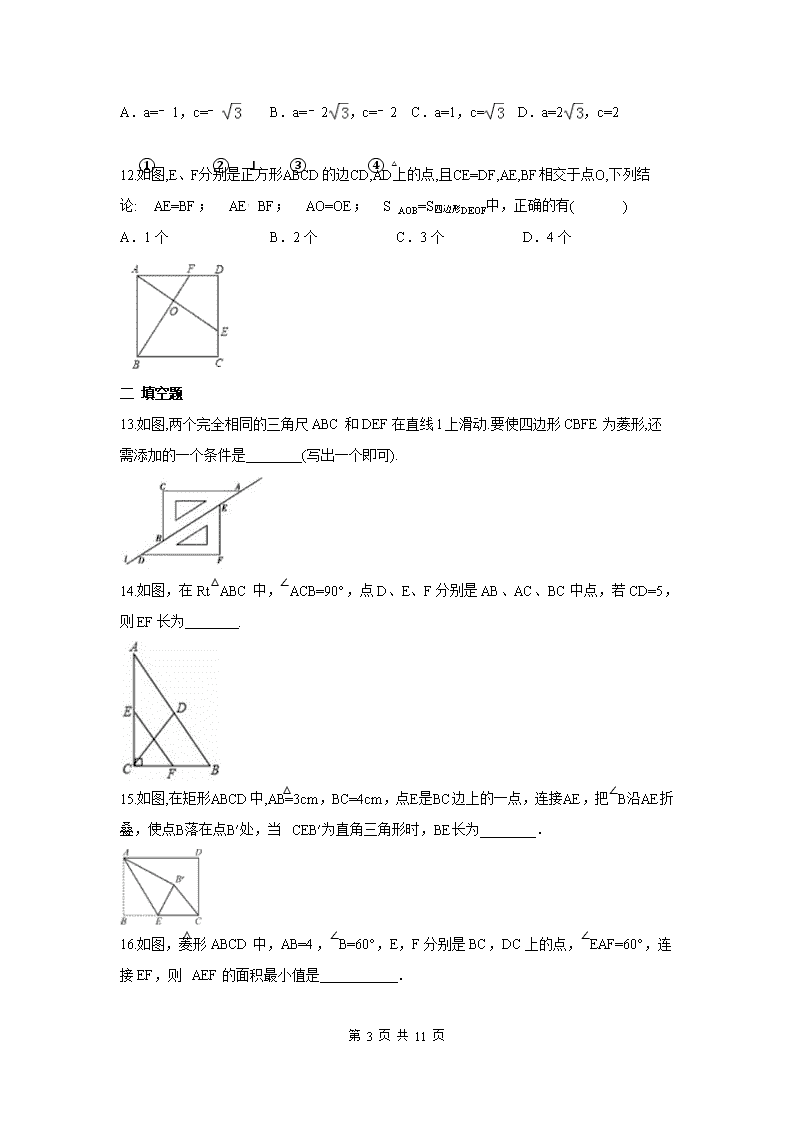12.如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结 论:①AE=BF；②AE⊥BF；③AO=OE；④S△AOB=S四边形DEOF中，正确的有( ) A．1 个 B．2 个 C．3 个 D．4 个 二 填空题 13.如图,两个完全相同的三角尺 ABC 和 DEF 在直线 l 上滑动.要使四边形 CBFE 为菱形,还需 添加的一个条件是________(写出一个即可). 14.如图，在 Rt△ABC 中，∠ACB=90°，点 D、E、F 分别是 AB、AC、BC 中点，若 CD=5， 则 EF 长为 . 15.如图,在矩形ABCD中,AB=3cm，BC=4cm，点E是BC边上的一点，连接AE，把∠B沿AE 折叠，使点B落在点B′处，当△CEB′为直角三角形时，BE长为________． 16.如图，菱形 ABCD 中，AB=4，∠B=60°，E，F 分别是 BC，DC 上的点，∠EAF=60°， 连接 EF，则△AEF 的面积最小值是 ． 第 4 页 共 11 页 17.如图，已知矩形纸片ABCD，点E是AB的中点，点G是BC上的一点，∠BEG＞60°，现沿 直线EG将纸片折叠，使点B落在纸片上的点H处，连接AH，则与∠BEG相等的角的个数为 ______个. 18.如图，已知正方形 ABCD 的边长为 10，点 P 是对角线 BD 上的一个动点，M、N 分别是 BC、CD 边上的中点，则 PM＋PN 的最小值是___________． 三 作图题 19.如图，将四边形 ABCD 放在每个小正方形的边长为 1 的网格中，点 A．B、C、D 均落在 格点上． （Ⅰ）计算 AD2+DC2+CB2 的值等于 ； （Ⅱ）请在如图所示的网格中，用无刻度的直尺，画出一个以 AB 为一边的矩形，使该矩形 的面积等于 AD2+DC2+CB2，并简要说明画图方法（不要求证明）． 四 解答题 20.如图，点 E、F 为线段 BD 的两个三等分点，四边形 AECF 是菱形． （1）试判断四边形 ABCD 的形状，并加以证明； 第 5 页 共 11 页 （2）若菱形 AECF 的周长为 20，BD 为 24，试求四边形 ABCD 的面积． 21.如图，已知在▱ ABCD中，E、F是对角线BD上的两点，且BF=DE．求证：AE=CF． 22.如图，在△ABC 中，AB=BC，BD 平分∠ABC．四边形 ABED 是平行四边形，DE 交 BC 于点 F，连接 CE．求证：四边形 BECD 是矩形． 第 6 页 共 11 页 23.如图，在△ABC 中，∠ACB=90°，BC 的垂直平分线 DE 交 BC 于 D，交 AB 于 E，F 在 DE 上，并且 AF=CE． （1）求证：四边形 ACEF 是平行四边形； （2）当∠B 满足什么条件时，四边形 ACEF 是菱形？请回答并证明你的结论． 24.将矩形ABCD折叠使A，C重合，折痕交BC于E，交AD于F， （1）求证：四边形AECF为菱形； （2）若AB=4，BC=8，求菱形的边长； （3）在（2）的条件下折痕EF的长． 第 7 页 共 11 页 25.如图，已知平行四边形 ABCD 的两条对角线相交于点 O，E 是 BO 的中点，过 B 点作 AC 的平行线，交 CE 的延长线于点 F，连接 BF （1）求证：FB=AO； （2）当平行四边形 ABCD 满足什么条件时，四边形 AFBO 是菱形？说明理由． 26.如图,△ABC 中,点 O 是边 AC 上一个动点,过 O 作直线 MN∥BC.设 MN 交∠ACB 的平分 线于点 E,交∠ACB 的外角平分线于点 F． （1）求证：OE=OF； （2）若 CE=12,CF=5,求 OC 的长； （3）当点 O 在边 AC 上运动到什么位置时,四边形 AECF 是矩形？并说明理由． 第 8 页 共 11 页 第十八章 平行四边形周周测 9 试题答案 1.C． 2.B．3.B. 4.A 5.C； 6.C 7.C； 8.B. 9.C 10.C. 11. 12.C. 13.C；B=BF 或 BE⊥CF 或∠EBF=60°或 BD=BF(答案不唯一) 14.5 15. 3 或 1.5 16. ． 17. 3 18.10 19.解：（1）∵AD2=32+12=10，DC2=32+12=10，CB2=12+12=2， ∴AD2+DC2+CB2=10+10=2=22，故答案为：22； （2）如图，以 AB 为边做正方形 ABGH，再作平行四边形 HMNG，直线 MN 交 AH 于点 Q， 交 GB 于点 P，矩形 ABPQ 即为所求．理由是：∵S▱ HMNG=2×6﹣2×（ +1+ ×5×1）=4， ∴S 矩形 HQNG=S▱ HMNG=4， ∵S 正方形 ABGH=（ ）2=26，∴S 矩形 ABPQ=26﹣4=22，所以画出的矩形 ABPQ 的面积等于 AD2+DC2+CB2． 第 9 页 共 11 页 20.解：（1）四边形 ABCD 为菱形．理由如下：如图，连接 AC 交 BD 于点 O， ∵四边形 AECF 是菱形，∴AC⊥BD，AO=OC，EO=OF， 又∵点 E、F 为线段 BD 的两个三等分点，∴BE=FD，∴BO=OD， ∵AO=OC，∴四边形 ABCD 为平行四边形，∵AC⊥BD，∴四边形 ABCD 为菱形； （2）∵四边形 AECF 为菱形，且周长为 20，∴AE=5，∵BD=24，∴EF=8，OE= EF= ×8=4， 由勾股定理得，AO= = =3，∴AC=2AO=2×3=6， ∴S 四边形 ABCD= BD•AC= ×24×6=72． 21.证明：连接AC交BD于点O，连接AF、CE ∵▱ ABCD∴OA=OC，OB=OD ∵OF=BF﹣OB，OE=DE﹣OD,BF=DE∴OE=OF ∵OA=OC，OE=OF ∴四边形AECF是平行四边形∴AE=CF 22.证明：∵AB=BC，BD 平分∠ABC，∴BD⊥AC，AD=CD． ∵四边形 ABED 是平行四边形，∴BE∥AD，BE=AD，∴BE=CD， ∴四边形 BECD 是平行四边形．∵BD⊥AC，∴∠BDC=90°，∴▱ BECD 是矩形． 23.解：（1）∵ED 是 BC 的垂直平分线∴EB=EC，ED⊥BC，∴∠3=∠4， ∵∠ACB=90°，∴FE∥AC，∴∠1=∠5， ∵∠2 与∠4 互余，∠1 与∠3 互余∴∠1=∠2，∴AE=CE， 又∵AF=CE，∴△ACE 和△EFA 都是等腰三角形，∴∠5=∠F，∴∠2=∠F， ∴在△EFA 和△ACE 中∵∠1=∠5,∠2=∠F,AF=CE，∴△EFA≌△ACE（AAS）， ∴∠AEC=∠EAF∴AF∥CE∴四边形 ACEF 是平行四边形； （2）当∠B=30°时，四边形 ACEF 是菱形．证明如下： ∵∠B=30°，∠ACB=90°∴∠1=∠2=60°∴∠AEC=60°∴AC=EC ∴平行四边形 ACEF 是菱形． 第 10 页 共 11 页 24. 25.证明：（1）如图，取 BC 的中点 G，连接 EG． ∵E 是 BO 的中点，∴EG 是△BFC 的中位线，∴EG=0.5BF．同理，EG=0.5OC，∴BF=OC． 又∵点 O 是▱ ABCD 的对角线交点，∴AO=CO，∴BF=AO． 又∵BF∥AC，即 BF∥AO，∴四边形 AOBF 为平行四边形，∴FB=AO； （2）当平行四边形 ABCD 是矩形时，四边形 AFBO 是菱形．理由如下： ∵平行四边形 ABCD 是矩形，∴OA=OB，∴平行四边形 AFBO 是菱形． 26.（1）证明：∵MN 交∠ACB 的平分线于点 E，交∠ACB 的外角平分线于点 F， ∴∠2=∠5，∠4=∠6，∵MN∥BC，∴∠1=∠5，∠3=∠6， ∴∠1=∠2，∠3=∠4，∴EO=CO，FO=CO，∴OE=OF； （2）解：∵∠2=∠5，∠4=∠6，∴∠2+∠4=∠5+∠6=90°， ∵CE=12，CF=5，∴EF= =13，∴OC= EF=6.5； （3）解：当点 O 在边 AC 上运动到 AC 中点时，四边形 AECF 是矩形． 证明：当 O 为 AC 的中点时，AO=CO，∵EO=FO，∴四边形 AECF 是平行四边形， ∵∠ECF=90°，∴平行四边形 AECF 是矩形． 第 11 页 共 11 页