江西专版2020中考数学复习方案第三单元函数第09课时平面直角坐标系与函数课件 36页

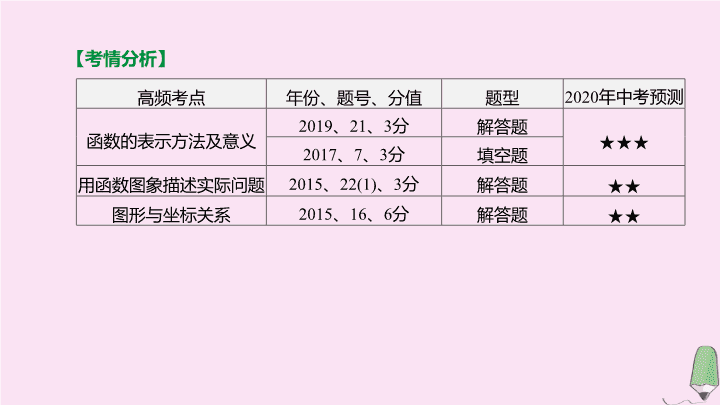
单元思维导图 第 9 课时 平面直角坐标系与函数 第三单元　函数 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 函数的 表示方法 及意义 2019 、 21 、 3 分 解答题 ★★★ 2017 、 7 、 3 分 填空题 用函数 图象描述 实际问题 2015 、 22(1) 、 3 分 解答题 ★★ 图形 与坐标 关系 2015 、 16 、 6 分 解答题 ★★ 1 . 各象限内点的坐标的符号特征 ( 如图 9-1) : 考点一　平面直角坐标系内点的坐标特征 考点聚焦 图 9-1 (-,+) (-,-) (+,-) 2 . 坐标轴上的点的坐标特征 : (1) 点 P ( x , y ) 在 x 轴上 ⇔ y= ④ 　　　　 ;  (2) 点 P ( x , y ) 在 y 轴上 ⇔ ⑤ 　　　　 = 0;  (3) 点 P ( x , y ) 既在 x 轴上 , 又在 y 轴上 ⇔ ⑥ 　　　　 .  0 x x=y= 0 【 温馨提示 】 坐标轴上的点不属于任何象限 . 3 . 平行于坐标轴的直线上的点的坐标特征 (1) 平行于 x 轴的直线上的点 ⇔ ⑦ 　　　　 坐标相同 , ⑧ 　　　　 坐标为不相等的实数 .  (2) 平行于 y 轴的直线上的点 ⇔ ⑨ 　　　　 坐标相同 , ⑩ 　　　　 坐标为不相等的实数 .  4 . 象限角平分线上点的坐标特征 (1) 点 P ( x , y ) 在第一、三象限的角平分线上 ⇔ x=y ; (2) 点 P ( x , y ) 在第二、四象限的角平分线上 ⇔ ⑪ 　　　　 .  纵 横 纵 横 y= - x 5 . 对称点的坐标特征 点 P ( x , y ) 关于 x 轴对称的点 P 1 的坐标为 ⑫ 　　　　 ;  点 P ( x , y ) 关于 y 轴对称的点 P 2 的坐标为 ⑬ 　　　　 ;  点 P ( x , y ) 关于原点对称的点 P 3 的坐标为 ⑭ 　　　　 .  规律可简记为 : 关于谁对称 , 谁不变 , 另一个变号 ; 关于原点对称都变号 . 图 9-2 ( x ,- y ) (- x , y ) (- x ,- y ) 6 . 点平移的坐标特征 P ( x , y ) P' ( x - a , y )[ 或 ( x + a , y )]; P ( x , y ) P″ ⑮ 　　 　   ( x , y + b )[ 或 ( x , y - b )] 1 . 点 P ( x , y ) 到 x 轴的距离为 ⑯ 　　　　 ; 到 y 轴的距离为 |x| ; 到原点的距离为 ⑰ 　　　　 .  2 . 若 P ( x 1 , y 1 ), Q ( x 2 , y 2 ), 则 PQ= ⑱ 　 　　　　 . 特别地 , PQ ∥ x 轴 ⇔ PQ= ⑲ 　　　　 ; PQ ∥ y 轴 ⇔ PQ= ⑳ 　　　　 .  考点二　点到坐标轴的距离 |y| |x 1 - x 2 | |y 1 - y 2 | 考点三　位置的确定 1 . 平面直角坐标系法 . 2 . 方向角 + 距离 . 考点四　函数基础知识 1 . 函数的概念 : 一般地 , 在一个变化过程中 , 如果有两个变量 x 与 y , 并且对于 x 的每一个确定的值 , y 都有唯一确定的值与之对应 , 那么我们就说 x 是自变量 , y 是 x 的函数 . 如果当 x=a 时 y=b , 那么 b 叫做当自变量的值为 a 时的函数值 . 2 . 函数的三种表示方法 : ㉑ 　　　　 法、 ㉒ 　　　　 法和 ㉓ 　　　　 法 .  3 . 用描点法画函数图象的一般步骤 : ㉔ 　　　　 → ㉕ 　　　　 → ㉖ 　　　　 .  解析式 列表 图象 列表 描点 连线 4 . 自变量的取值范围 不等于 0 大于或等于 0 【 温馨提示 】 实际问题中自变量的取值还要符合变量的实际意义 . 1 . [2019· 株洲 ] 在平面直角坐标系中 , 点 A (2,-3) 位于 ( 　　 ) A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限 2 . [2019· 甘肃 ] 已知点 P ( m +2,2 m -4) 在 x 轴上 , 则点 P 的坐标是 ( 　　 ) A . (4,0) B . (0,4) C . (-4,0) D . (0,-4) 题组一　必会题 对点演练 D A 3 . 若将点 A (1,3) 向左平移 2 个单位长度 , 再向下平移 4 个单位长度得到点 B , 则点 B 的坐标为 ( 　　 ) A . (-2,-1) B . (-1,0) C . (-1,-1) D . (-2,0) C D 5 . [2019· 随州 ] 第一次 “ 龟兔赛跑 ”, 兔子因为在途中睡觉而输掉比赛 , 很不服气 , 决定与乌龟再比一次 , 并且骄傲地说 , 这次我一定不睡觉 , 让乌龟先跑一段距离我再去追都可以赢 . 结果兔子又一次输掉了比赛 , 则下列函数图象可以体现这次比赛过程的是 ( 　　 ) 图 9-3 B 6 . 如图 9-4 是轰炸机机群的一个飞行队形 , 如果最后两架轰炸机的平面坐标分别为 A (-2,1) 和 B (-2,-3), 那么第一架轰炸机 C 的平面坐标是 　　　　 .  (2,-1) 图 9-4 7 . 若点 P ( a , b ) 到 x 轴的距离是 3, 到 y 轴的距离是 5, 则这样的点 P 共有 ( 　　 ) A . 1 个 B . 2 个 C . 3 个 D . 4 个 题组二　易错题 【 失分点 】 不理解或记混点的坐标是一对有序实数 ; 点坐标与该点到坐标轴的距离的关系不明确 , 忽视函数中两变量与点的坐标关系 , 忽视自变量的取值范围还要符合实际意义 . D C 考向一　平面直角坐标系中点的坐标特征 (3,0) 例 1 在平面直角坐标系中 , 四边形 ABCD 的三个顶点的坐标分别是 A (-1,0), B (-1,-2), C (3,2 a -1), 且点 C 在第四象限的角平分线上 , AB ∥ CD , 点 D 在 x 轴上 , 线段 CB 交 y 轴于点 E. (1) 点 D 的坐标为 　　　　 , a= 　　　　 ;  (2) 试求 △ ABE 和四边形 ABCD 的面积 . -1 例 1 在平面直角坐标系中 , 四边形 ABCD 的三个顶点的坐标分别是 A (-1,0), B (-1,-2), C (3,2 a -1), 且点 C 在第四象限的角平分线上 , AB ∥ CD , 点 D 在 x 轴上 , 线段 CB 交 y 轴于点 E. (2) 试求 △ ABE 和四边形 ABCD 的面积 . | 考向精练 | 1 . 若点 P ( a ,4- a ) 是第二象限的点 , 则 a 必须满足 ( 　　 ) A .a< 4 B .a> 4 C .a< 0 D . 0