- 823.50 KB
- 2021-11-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
专题跟踪突破一 规律探索型问题
一、选择题
(
每小题
6
分
,
共
30
分
)
1
.
(
2013
·
泰安
)
观察下列等式:
3
1
=
3
,
3
2
=
9
,
3
3
=
27
,
3
4
=
81
,
3
5
=
243
,
3
6
=
729
,
3
7
=
2187
,
…
解答下列问题:
3
+
3
2
+
3
3
+
3
4
+
…
+
3
2013
的末位数字是
(
)
A
.
0
B
.
1
C
.
3
D
.
7
C
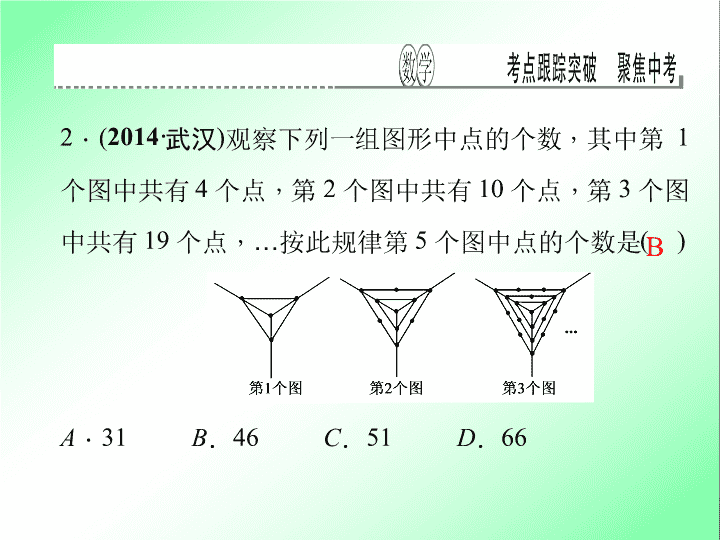
2
.
(
2014·
武汉
)
观察下列一
组图形中点的个数
,
其中第
1
个图中共有
4
个点
,
第
2
个图中共有
10
个点
,
第
3
个图
中共有
19
个点
,
…
按此规律第
5
个图中点的个数是
(
)
A
.
31
B
.
46
C
.
51
D
.
66
B
3
.
(
2014
·
十堰
)
根据如图中箭头的指向规律
,
从
2013
到
2014
再到
2015
,
箭头的方向是以下图示中的
(
)
.
A
.
B
.
C
.
D
.
D
4
.
(
2014·
重庆
)
下列图形都是按照一定规律组成
,
第一个
图形中共有
2
个三角形
,
第二个图形中共有
8
个三角形
,
第三个图形中共有
14
个三角形
,
…
,
依此规律
,
第五个
图形中三角形的个数是
(
)
A
.
22
B
.
24
C
.
26
D
.
28
C
5
.
(
2014·
内江
)
如图
,
已知
A
1
,
A
2
,
A
3
,
…
,
A
n
,
A
n
+
1
是
x
轴上的
点
,
且
OA
1
=
A
1
A
2
=
A
2
A
3
=
…
=
A
n
A
n
+
1
=
1
,
分别过点
A
1
,
A
2
,
A
3
,
…
,
A
n
,
A
n
+
1
作
x
轴的垂线交直线
y
=
2x
于点
B
1
,
B
2
,
B
3
,
…
,
B
n
,
B
n
+
1
,
连接
A
1
B
2
,
B
1
A
2
,
B
2
A
3
,
…
,
A
n
B
n
+
1
,
B
n
A
n
+
1
,
依次相交于
点
P
1
,
P
2
,
P
3
,
…
,
P
n
.
△
A
1
B
1
P
1
,
△
A
2
B
2
P
2
,
△
A
n
B
n
P
n
的面积依次
记为
S
1
,
S
2
,
S
3
,
…
,
S
n
,
则
S
n
为
(
)
A
.
n
+
1
2n
+
1
B
.
n
3n
-
1
C
.
n
2
2n
-
1
D
.
n
2
2n
+
1
D
二、填空题
(
每小题
6
分
,
共
30
分
)
6
.
(
2014·
毕节
)
观察下列一组数:
1
4
,
3
9
,
5
16
,
7
25
,
9
36
,
…
,
它们是按一定规律排列的
,
那么这一组数的第
n
个数是
.
7
.
(
2014
·
娄底
)
如图是一组有规律的图案
,
第一个图案由
4
个
▲
组成
,
第二个图案由
7
个
▲
组成
,
第三个图案由
10
个
▲
组成
,
第四个图案由
13
个
▲
组成
,
…
,
则第
n(n
为正整数
)
个图案由
____
个
▲
组成.
3n
+
1
8
.
(
2014
·
梅州
)
如图
,
弹性小球从点
P(0
,
3)
出发
,
沿所示方向运动
,
每当小球碰到矩形
OABC
的边时反弹
,
反弹时反射角等于入射角
,
当小球第
1
次碰到矩形的边时的点为
P
1
,
第
2
次碰到矩形的边时的点为
P
2
,
…
,
第
n
次碰到矩形的边时的点为
P
n
,
则点
P
3
的坐标是
;点
P
2014
的坐标是
.
(8
,
3)
(5
,
0)
9
.
(
2014·
菏泽
)
下面是一个按照某种规律排列的数阵:
根据数阵的规律
,
第
n(n
是整数
,
且
n
≥
3)
行从左到右数
第
n
-
2
个数是
.
(
用含
n
的代数式表示
)
10
.
(
2013
·
潍坊
)
当白色小正方形个数依次等于
1
,
4
,
9
…
时
,
由白色小正方形和黑色小正方形组成的图形分别如图所示.则第
n
个图形中白色小正方形和黑色小正方形的个数总和等于
.
(
用
n
表示
,
n
是正整数
)
n
2
+
4n
三、解答题
(
共
40
分
)
11
.
(12
分
)
(
2014
·
宜宾
)
在平面直角坐标系中
,
若点
P(x
,
y)
的坐标
x
,
y
均为整数
,
则称点
P
为格点
,
若一个多边形的面积记为
S
,
其内部的格点数记为
N
,
边界上的格点数记为
L
,
例如图中
△
ABC
是格点三角形
,
对应的
S
=
1
,
N
=
0
,
L
=
4.
(1)
求出图中格点四边形
DEFG
对应的
S
,
N
,
L
;
(2)
已知格点多边形的面积可表示为
S
=
N
+
aL
+
b
,
其中
a
,
b
为常数
,
若某格点多边形对应的
N
=
82
,
L
=
38
,
求
S
的值.
解:
(1)
观察图形
,
可得
S
=
3
,
N
=
1
,
L
=
6
(2)
根据格点三角形
ABC
及格点四边形
DEFG
中的
S
,
N
,
L
的值可得
,
î
ï
í
ï
ì
4a
+
b
=
1
,
1
+
6a
+
b
=
3
,
解得
î
ï
í
ï
ì
a
=
1
2
,
b
=-
1
,
∴
S
=
N
+
1
2
L
-
1
,
将
N
=
82
,
L
=
38
代入可得
S
=
82
+
1
2
×
38
-
1
=
100
12
.
(
12
分
)
(
2012·
宁波
)
用同样大小的黑色棋子按如图所示
的规律摆放:
(
1
)
第
5
个图形有多少颗黑色棋子?
(
2
)
第几个图形有
2013
颗黑色棋子?请说明理由
.
解:
(1)
寻找规律:第一个图需棋子
6
=
3
×
2
,
第二个图需棋子
9
=
3
×
3
,
第三个图需棋子
12
=
3
×
4
,
第四个图需棋子
15
=
3
×
5
,
∴
第五个图需棋子
3
×
6
=
18.
答:第
5
个图形有
18
颗黑色棋子
(2)
由
(1)
可得
,
第
n
个图需棋子
3(n
+
1)
颗
,
设第
n
个图形有
2013
颗黑色棋子
,
则
3(n
+
1)
=
2013
,
解得
n
=
670.
答:第
670
个图形有
2013
颗黑色棋子
13
.
(16
分
)
(
2014
·
凉山州
)
实验与探究:三角点阵前
n
行的点数计算.
如图是一个三角点阵
,
从上向下数有无数多行
,
其中第一行有
1
个点
,
第二行有
2
个点
…
第
n
行有
n
个点
…
容易发现
,
10
是三角点阵中前
4
行的点数的和
,
你能发现
300
是前多少行的点数的和吗?
如果要用试验的方法
,
由上而下地逐行的相加其点数
,
虽然你能发现
1
+
2
+
3
+
4
+
…
+
23
+
24
=
300.
得知
300
是前
24
行的点数的和
,
但是这样寻找答案需我们先探求三角点阵中前
n
行的点数的和与
n
的数量关系是
1
+
2
+
3
+
…
+
(n
-
2)
+
(n
-
1)
+
n
,
可以发现.
2
×
[1
+
2
+
3
+
4
+
…
+
(n
-
2)
+
(n
-
1)
+
n]
=
[1
+
2
+
3
+
…
+
(n
-
2)
+
(n
-
1)
+
n]
+
[n
+
(n
-
1)
+
(n
-
2)
+
(n
-
3)
+
…
+
3
+
2
+
1]
.
把两个中括号中的第一项相加
,
第二项相加
…
第
n
项相加
,
上式等
号的后边变形为这
n
个小括号都等于
n
+
1
,
整个式子等于
n
(
n
+
1
)
,
于是得到
1
+
2
+
3
+
…
+
(
n
-
2
)
+
(
n
-
1
)
+
n
=
1
2
n
(
n
+
1
)
,
这就是说
,
三角点阵中前
n
项的点数的和是
1
2
n
(
n
+
1
)
.
下列用一元二
次方程解决上述问题:
设三角点阵中前
n
行的点数的和为
300
,
则有
1
2
n
(
n
+
1
)
整理这个方程
,
得
n
2
+
n
-
600
=
0
,
解方程得
n
1
=
24
,
n
2
=-
25.
根据问题中未知数的意义确定
n
=
24
,
即三角点阵中前
24
行的点数的和是
300.
请你根据上述材料回答下列问题:
(1)
三角点阵中前
n
行的点数的和能是
600
吗?如果能
,
求出
n
;如果不能
,
试用一元二次方程说明道理.
(2)
如果把图中的三角点阵中各行的点数依次换成
2
,
4
,
6
,
…
,
2n
,
…
,
你能探究出前
n
行的点数的和满足什么规律吗?这个三角点阵中前
n
行的点数的和能是
600
吗?如果能
,
求出
n
;如果不能
,
试用一元二次方程说明道理.
相关文档
- 福建专版2020中考数学复习方案第一2021-11-107页
- 福建专版2020中考数学复习方案第三2021-11-1034页
- 中考数学复习:解直角三角形的实际应2021-11-1043页
- 2020中考数学复习基础小卷速测十一2021-11-106页
- 鄂尔多斯专版2020中考数学复习方案2021-11-078页
- 呼和浩特专版2020中考数学复习方案2021-11-079页
- 2020中考数学复习基础小卷速测(一)2021-11-073页
- 鄂尔多斯专版2020中考数学复习方案2021-11-0729页
- 江西专版2020中考数学复习方案第四2021-11-078页
- 江西专版2020中考数学复习方案第六2021-11-0769页