河北省石家庄市启明学校2020-2021学年第一学期九年级数学期末模拟测试题（五） 35页

河北省石家庄市启明学校 2020-2021 学年第一学期九年级数学期末模拟测试题（五） 一、选择题（本大题共 14 个小题，共 34 分.1～8 小题各 3 分，9～14 小题各 2 分.在每小题 给出的四个选项中只有一项是符合题目要求的） 1．（3 分）一元二次方程 2x2+3x﹣4＝0 的二次项系数、一次项系数、常数项分别是（ ） A．2，﹣3，﹣4 B．2，3，4 C．2，﹣3，4 D．2，3，﹣4 2．（3 分）计算：（ ）﹣1﹣tan60°•cos30°＝（ ） A．﹣ B．1 C． D． 3．（3 分）如图， ⊙ O 是△ABC 的外接圆，∠OCB＝40°，则∠A 的大小为（ ） A．40° B．50° C．80° D．100° 4．（3 分）如图，△ABC 中，DE∥BC，AD：DB＝1：2，下列选项正确的是（ ） A．DE：BC＝1：2 B．AE：AC＝1：3 C．BD：AB＝1：3 D．S△ADE：S△ABC＝1：4 5．（3 分）为了估计某地区供暖期间空气质量情况，某同学在 20 天里做了如下记录： 其中 ω ＜50 时空气质量为优，50≤ ω ≤100 时空气质量为良，100＜ ω ≤150 时空气质量为 轻度污染．若按供暖期 125 天计算，请你估计该地区在供暖期间空气质量达到良以上（含 良）的天数为（ ） 污染指数 （ ω ） 40 60 80 100 120 140 天数（天） 3 2 3 4 5 3 A．75 B．65 C．85 D．100 6．（3 分）反比例函数 y＝ 的图象如图所示，以下结论： ① 常数 m＜﹣2； ② 若 A（﹣1，h），B（2，k）在图象上，则 h＜k； ③ y 随 x 的增大而减小； ④ 若 P（x，y）在图象上，则 P'（﹣x，﹣y）也在图象上． 其中正确的是（ ） A． ①② B． ③④ C． ②③ D． ②④ 7．（3 分）如图，是小孔成像原理的示意图，根据图所标注的尺寸，这支蜡烛在暗盒中所成 的像 CD 的长是（ ） A． B． C． D．1 cm 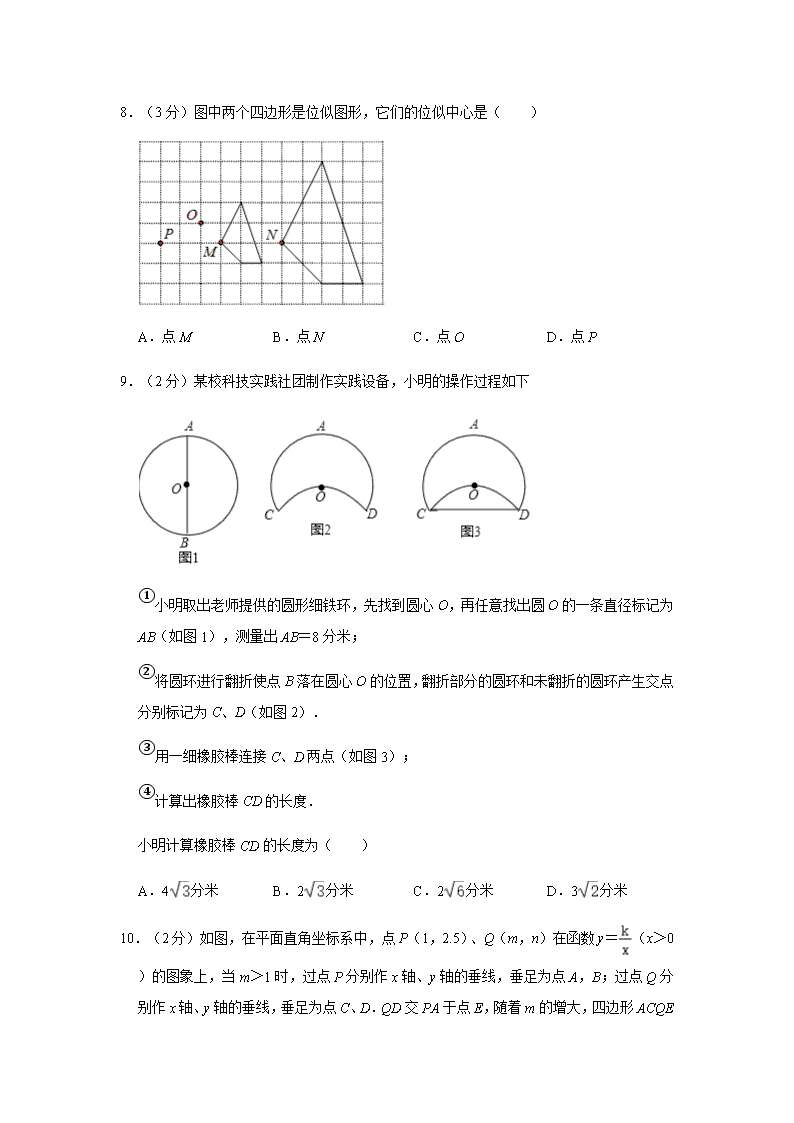8．（3 分）图中两个四边形是位似图形，它们的位似中心是（ ） A．点 M B．点 N C．点 O D．点 P 9．（2 分）某校科技实践社团制作实践设备，小明的操作过程如下 ① 小明取出老师提供的圆形细铁环，先找到圆心 O，再任意找出圆 O 的一条直径标记为 AB（如图 1），测量出 AB＝8 分米； ② 将圆环进行翻折使点 B 落在圆心 O 的位置，翻折部分的圆环和未翻折的圆环产生交点 分别标记为 C、D（如图 2）． ③ 用一细橡胶棒连接 C、D 两点（如图 3）； ④ 计算出橡胶棒 CD 的长度． 小明计算橡胶棒 CD 的长度为（ ） A．4 分米 B．2 分米 C．2 分米 D．3 分米 10．（2 分）如图，在平面直角坐标系中，点 P（1，2.5）、Q（m，n）在函数 y＝ （x＞0） 的图象上，当 m＞1 时，过点 P 分别作 x 轴、y 轴的垂线，垂足为点 A，B；过点 Q 分别 作 x 轴、y 轴的垂线，垂足为点 C、D．QD 交 PA 于点 E，随着 m 的增大，四边形 ACQE 的面积（ ） A．增大 B．先增大后减小 C．先减小后增大 D．减小 11．（2 分）在湖边高出水面 40m 的山顶 A 处看见一架无人机停留在湖面上空某处，观察到 无人机底部标志 P 处的仰角为 45°，又观其在湖中之像的俯角为 60°，则无人机底部 P 距离湖面的高度是（ ） A．（40 +40）m B．（40 +80）m C．（50 +100）m D．（50 +50）m 12．（2 分）如图，△ABC 中，∠A＝78°，AB＝4，AC＝6．将△ABC 沿图示中的虚线剪开， 剪下的阴影三角形与原三角形不相似的是（ ） A． B． C． D． 13．（2 分）如图，一圆弧过方格的格点 A、B、C，在方格中建立平面直角坐标系，使点 A 的坐标为（﹣3，2），则该圆弧所在圆心坐标是（ ） A．（0，0） B．（﹣2，1） C．（﹣2，﹣1） D．（0，﹣1） 14．（2 分）如图，在边长为 1 的正方形 ABCD 中，动点 F，E 分别以相同的速度从 D，C 两 点同时出发向 C 和 B 运动（任何一个点到达即停止），连接 AE、BF 交于点 P，过点 P 作 PM∥CD 交 BC 于 M 点，PN∥BC 交 CD 于 N 点，连接 MN，在运动过程中则下列结 论： ① △ABE≌△BCF； ② AE＝BF； ③ AE⊥BF； ④ CF2＝PE•BF； ⑤ 线段 MN 的最小 值为 ．其中正确的结论有（ ） A．2 个 B．3 个 C．4 个 D．5 个 二、填空题（共 4 小题，每小题 3 分，满分 12 分） 15．（3 分）若 ＝ ，则 ＝ ． 16．（3 分）如图，已知圆锥的高为 8，底面圆的直径为 12，则此圆锥的侧面积是 ． 17．（3 分）某商品售价 y（元/件）是基础价与浮动价的和，其中基础价保持不变，浮动价 与月需求量 x（件）成反比例根据表格写出 y 与 x 的函数关系式 ． 售价 y（元/件） 11 10 需求量 x（件/月） 100 120 18．（3 分）如图所示，n+1 个直角边长为 3 的等腰直角三角形△AB1C1，△C1B2C2……，斜 边在同一直线上，设△B2D1C1 的面积为 S1，△B3D2C2 的面积为 S2，…，△Bn+1Dn ∁ n 的面 积为 Sn，则 S1＝ ；S2＝ ；Sn＝ ． 三、解答题（本大题共 6 个大题，共 54 分，解答应写出文字说明、证明过程或演算步骤） 19．（8 分）已知关于 x 的一元二次方程 kx2﹣4x+2＝0 有两个不相等的实数根． （1）求实数 k 的取值范围； （2）写出满足条件的 k 的最大整数值，并求此时方程的根． 20．（8 分）我区某中学开展“社会主义核心价值观”演讲比赛活动，九（1）、九（2）班根 据初赛成绩各选出 5 名选手参加复赛，两个班各选出的 5 名选手的复赛成绩（满分为 100 分）如图所示．根据图中数据解决下列问题： （1）九（1）班复赛成绩的中位数是 分，九（2）班复赛成绩的众数是 分； （2）小明同学已经算出了九（1）班复赛的平均成绩 ＝85 分； 方差 S2＝ [（85﹣85）2+（75﹣85）2+（80﹣85）2+（85﹣85）2+（100﹣85）2]＝70（分 2）， 请你求出九（2）班复赛的平均成绩 和方差 S22； （3）根据（2）中计算结果，分析哪个班级的复赛成绩较好？ 21．（8 分）如图，一次函数 y＝ax+b（a≠0）的图象与反比例函数 y＝ （k≠0）的图象相 交于 A、B 两点且点 A 的坐标为（3，1），点 B 的坐标（﹣1，n）． （1）分别求两个函数的解析式； （2）求△AOB 的面积． 22．（10 分）如图，点 G 是边长为 4 的正方形 ABCD 的边 BC 上的一点，矩形 DEFG 的边 EF 过点 A，GD＝5． （1）寻找并证明图中的两组相似三角形； （2）求 HG、FG 的长． 23．（10 分）随着正定旅游业的快速发展，外来游客对住宿的需求明显增大，某宾馆拥有的 床位数不断增加． （1）该宾馆床位数从 2016 年底的 200 个增长到 2018 年底的 288 个，求该宾馆这两年（从 2016 年底到 2018 年底）拥有的床位数的年平均增长率； （2）根据市场表现发现每床每日收费 40 元，288 张床可全部租出，若每床每日收费提 高 10 元，则租出床位减少 20 张．若想平均每天获利 14880 元，同时又减轻游客的经济 负担每张床位应定价多少元？ 24．（10 分）如图，点 A 在数轴上对应的数为 20，以原点 O 为圆心，OA 为半径作优弧 ， 使点 B 在 O 右下方，且 tan∠AOB＝ ，在优弧 上任取一点 P，且能过 P 作直线 l∥ OB 交数轴于点 Q，设 Q 在数轴上对应的数为 x，连接 OP． （1）若优弧上一段 的长为 10 π ，求∠AOP 的度数及 x 的值． （2）若线段 PQ 的长为 10，求这时 x 的值． 参考答案与试题解析 一、选择题（本大题共 14 个小题，共 34 分.1～8 小题各 3 分，9～14 小题各 2 分.在每小题 给出的四个选项中只有一项是符合题目要求的） 1．（3 分）一元二次方程 2x2+3x﹣4＝0 的二次项系数、一次项系数、常数项分别是（ ） A．2，﹣3，﹣4 B．2，3，4 C．2，﹣3，4 D．2，3，﹣4 【分析】根据一元二次方程的一般形式：ax2+bx+c＝0（a，b，c 是常数且 a≠0）中，ax2 叫二次项，bx 叫一次项，c 是常数项．其中 a，b，c 分别叫二次项系数，一次项系数， 常数项，直接进行判断即可． 【解答】解：一元二次方程 2x2+3x﹣4＝0 的二次项系数、一次项系数、常数项分别是 2， 3，﹣4． 故选：D． 2．（3 分）计算：（ ）﹣1﹣tan60°•cos30°＝（ ） A．﹣ B．1 C． D． 【分析】直接利用负指数幂的性质以及特殊角的三角函数值代入求出答案． 【解答】解：原式＝2﹣ × ＝2﹣ ＝ ． 故选：C． 3．（3 分）如图， ⊙ O 是△ABC 的外接圆，∠OCB＝40°，则∠A 的大小为（ ） A．40° B．50° C．80° D．100° 【分析】根据圆周角定理即可求出答案 【解答】解：∵OB＝OC ∴∠BOC＝180°﹣2∠OCB＝100°， ∴由圆周角定理可知：∠A＝ ∠BOC＝50° 故选：B． 4．（3 分）如图，△ABC 中，DE∥BC，AD：DB＝1：2，下列选项正确的是（ ） A．DE：BC＝1：2 B．AE：AC＝1：3 C．BD：AB＝1：3 D．S△ADE：S△ABC＝1：4 【分析】由 DE∥BC，易得△ADE∽△ABC，再由 AD：DB＝1：2，推出 AD：AB＝1：3， 据此求出 DE：BC，AE：AC，BD：AB，S△ADE：S△ABC，从而得出正确选项． 【解答】解：已知 AD：DB＝1：2， ∴AD：AB＝1：3，BD：AB＝2：3， ∵△ABC 中，DE∥BC， ∴△ADE∽△ABC， ∴AE：AC＝AD：AB＝DE：BC＝1：3， S△ADE：S△ABC＝（1：3）2＝1：9， 所以只有 B 正确． 故选：B． 5．（3 分）为了估计某地区供暖期间空气质量情况，某同学在 20 天里做了如下记录： 其中 ω ＜50 时空气质量为优，50≤ ω ≤100 时空气质量为良，100＜ ω ≤150 时空气质量为 轻度污染．若按供暖期 125 天计算，请你估计该地区在供暖期间空气质量达到良以上（含 良）的天数为（ ） 污染指数 （ ω ） 40 60 80 100 120 140 天数（天） 3 2 3 4 5 3 A．75 B．65 C．85 D．100 【分析】20 天中空气质量达到良以上的有 12 天，即所占比例为 ＝ ，然后乘以 125 即可求出供暖期间空气质量达到良以上（含良）的天数． 【解答】解：∵在被抽查的样本中空气质量达到良以上（含良）的天数所占百分比为 ×100%＝60%， ∴估计该地区在供暖期间空气质量达到良以上（含良）的天数为 125×60%＝75（天）， 故选：A． 6．（3 分）反比例函数 y＝ 的图象如图所示，以下结论： ① 常数 m＜﹣2； ② 若 A（﹣1，h），B（2，k）在图象上，则 h＜k； ③ y 随 x 的增大而减小； ④ 若 P（x，y）在图象上，则 P'（﹣x，﹣y）也在图象上． 其中正确的是（ ） A． ①② B． ③④ C． ②③ D． ②④ 【分析】根据反比例函数的性质得到 m＞0，则可对 ①③ 进行判断；根据反比例函数图 象上点的坐标特征对 ③④ 进行判断． 【解答】解：∵反比例函数图象经过第一、三象限， ∴m＞0，所以 ① 错误； 在每一象限，y 随 x 的增大而减小，所以 ③ 错误； ∵A（﹣1，h），B（2，k）在图象上， ∴h＝﹣m，k＝ ， 而 m＞0， ∴h＜k，所以 ② 正确； ∵m＝xy＝（﹣x）•（﹣y）， ∴若 P（x，y）在图象上，则 P'（﹣x，﹣y）也在图象上，所以 ④ 正确． 故选：D． 7．（3 分）如图，是小孔成像原理的示意图，根据图所标注的尺寸，这支蜡烛在暗盒中所成 的 像 CD 的长是（ ） A． B． C． D．1 cm 【分析】据小孔成像原理可知△AOB∽△COD，利用它们的对应边成比例就可以求出 CD 之长． 【解答】解：如图过 O 作直线 OE⊥AB，交 CD 于 F， 依题意 AB∥CD ∴OF⊥CD ∴OE＝12，OF＝2 而 AB∥CD 可以得△AOB∽△COD ∵OE，OF 分别是它们的高 ∴ ， ∵AB＝6， ∴CD＝1， 故选：D． 8．（3 分）图中两个四边形是位似图形，它们的位似中心是（ ） A．点 M B．点 N C．点 O D．点 P 【分析】根据位似变换的定义：对应点的连线交于一点，交点就是位似中心．即位似中 心一定在对应点的连线上． 【解答】解：点 P 在对应点 M 和点 N 所在直线上，再利用连接另两个对应点，得出相交 于 P 点，即可得出 P 为两图形位似中心， 故选：D． 9．（2 分）某校科技实践社团制作实践设备，小明的操作过程如下 ① 小明取出老师提供的圆形细铁环，先找到圆心 O，再任意找出圆 O 的一条直径标记为 AB（如图 1），测量出 AB＝8 分米； ② 将圆环进行翻折使点 B 落在圆心 O 的位置，翻折部分的圆环和未翻折的圆环产生交点 分别标记为 C、D（如图 2）． ③ 用一细橡胶棒连接 C、D 两点（如图 3）； ④ 计算出橡胶棒 CD 的长度． 小明计算橡胶棒 CD 的长度为（ ） A．4 分米 B．2 分米 C．2 分米 D．3 分米 【分析】作 OE⊥CD 于 E 交 ⊙ O 于 F．证明△OCF 是等边三角形即可解决问题． 【解答】解：作 OE⊥CD 于 E 交 ⊙ O 于 F． ∵CD 垂直平分 OF， ∴CO＝CF， ∴CO＝CF＝OF， ∴△OCF 是等边三角形， ∵OC＝4， ∴CE＝OC•cos30°＝2 ， ∵OE⊥CD， ∴CE＝ED， ∴CD＝2CE＝4 ， 故选：A． 10．（2 分）如图，在平面直角坐标系中，点 P（1，2.5）、Q（m，n）在函数 y＝ （x＞0） 的图象上，当 m＞1 时，过点 P 分别作 x 轴、y 轴的垂线，垂足为点 A，B；过点 Q 分别 作 x 轴、y 轴的垂线，垂足为点 C、D．QD 交 PA 于点 E，随着 m 的增大，四边形 ACQE 的面积（ ） A．增大 B．先增大后减小 C．先减小后增大 D．减小 【分析】首先利用 m 和 n 表示出 AC 和 CQ 的长，则四边形 ACQE 的面积即可利用 m、n 表示，然后根据函数的性质判断． 【解答】解：由题意可得：AC＝m﹣1，CQ＝n 则 S 四边形 ACQE＝AC•CQ＝（m﹣1）n＝mn﹣n ∵P（1，2.5）、Q（m，n）在函数 的图象上， ∴mn＝k＝2.5（常数） ∴S 四边形 ACQE＝2.5﹣n ∴当 m＞1 时，n 随 m 的增大而减小， ∴S 四边形 ACQE＝2.5﹣n 随 m 的增大而增大 故选：A． 11．（2 分）在湖边高出水面 40m 的山顶 A 处看见一架无人机停留在湖面上空某处，观察到 无人机底部标志 P 处的仰角为 45°，又观其在湖中之像的俯角为 60°，则无人机底部 P 距离湖面的高度是（ ） A．（40 +40）m B．（40 +80）m C．（50 +100）m D．（50 +50）m 【分析】设 AE＝x，则 PE＝AE＝x，根据山顶 A 处高出水面 40m，得出 OE＝40，OP′ ＝x+40，根据∠P′AE＝60°，得出 P′E＝ x，从而列出方程，求出 x 的值即可． 【解答】解：设 AE＝xm， 在 Rt△AEP 中∠PAE＝45°，则∠P＝45°， ∴PE＝A E＝x， ∵山顶 A 处高出水面 40m， ∴OE＝40m， ∴OP′＝OP＝PE+OE＝x+40， ∵∠P′AE＝60°， ∴P′E＝tan60°•AE＝ x， ∴OP′＝P′E﹣OE＝ x﹣40， ∴x+40＝ x﹣40， 解得：x＝40（ +1）， ∴PO＝PE+OE＝40（ +1）+40＝40 +80（m）， 即无人机距湖面的高度是（40 +80）m． 故选：B． 12．（2 分）如图，△ABC 中，∠A＝78°，AB＝4，AC＝6．将△ABC 沿图示中的虚线剪开， 剪下的阴影三角形与原三角形不相似的是（ ） A． B． C． D． 【分析】根据相似三角形的判定定理对各选项进行逐一判定即可． 【解答】解：A、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选 项错误； B、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项错误； C、两三角形的对应边不成比例，故两三角形不相似，故本选项正确； D、两三角形对应边成比例（4﹣1）：6＝（6﹣4）：4 且夹角相等，故两三角形相似，故 本选项错误． 故选：C ． 13．（2 分）如图，一圆弧过方格的格点 A、B、C，在方格中建立平面直角坐标系，使点 A 的坐标为（﹣3，2），则该圆弧所在圆心坐标是（ ） A．（0，0） B．（﹣2，1） C．（﹣2，﹣1） D．（0，﹣1） 【分析】根据垂径定理可得：分别作 AC 与 AB 的垂直平分线，相交于点 O，则点 O 即是 该圆弧所在圆的圆心．然后由点 A 的坐标为（﹣3，2），即可得到点 O 的坐标． 【解答】解：如图：分别作 AC 与 AB 的垂直平分线，相交于点 O， 则点 O 即是该圆弧所在圆的圆心． ∵点 A 的坐标为（﹣3，2）， ∴点 O 的坐标为（﹣2，﹣1）． 故选：C． 14．（2 分）如图，在边长为 1 的正方形 ABCD 中，动点 F，E 分别以相同的速度从 D，C 两 点同时出发向 C 和 B 运动（任何一个点到达即停止），连接 AE、BF 交于点 P，过点 P 作 PM∥CD 交 BC 于 M 点，PN∥BC 交 CD 于 N 点，连接 MN，在运动过程中则下列结 论： ① △ABE≌△BCF； ② AE＝BF； ③ AE⊥BF； ④ CF2＝PE•BF； ⑤ 线段 MN 的最小 值为 ．其中正确的结论有（ ） A．2 个 B．3 个 C．4 个 D．5 个 【分析】由正方形的性质及条件可判断出 ① △ABE≌△BCF，即可判断出 ② AE＝BF，∠ BAE＝∠CBF，再根据∠BAE+∠BEA＝90°，可得 ∠CBF+∠BEA＝90°，可得出∠APB ＝90°，即可判断 ③ ，由△BPE∽△BCF，利用相似三角形的性质，结合 CF＝BE 可判 断 ④ ；然后根据点 P 在运动中保持∠APB＝90°，可得点 P 的路径是一段以 AB 为直径 的弧，设 AB 的中点为 G，连接 CG 交弧于点 P，此时 CP 的长度最小，最后在 Rt△BCG 中，根据勾股定理，求出 CG 的长度，再求出 PG 的长度，即可求出线段 CP 的最小值， 可判断 ⑤ ． 【解答】解：∵动点 F，E 的速度相同， ∴DF＝CE， 又∵CD＝BC， ∴CF＝BE， 在△ABE 和△BCF 中， ∴△ABE≌△BCF（SAS），故 ① 正确； ∴∠BAE＝∠CBF，AE＝BF，故 ② 正确； ∵∠BAE+∠BEA＝90°， ∴∠CBF+∠BEA＝90°， ∴∠APB＝90°，故 ③ 正确； 在△BPE 和△BCF 中， ∵∠BPE＝∠BCF，∠PBE＝∠CBF， ∴△BPE∽△BCF， ∴ ， ∴CF•BE＝PE•BF， ∵CF＝BE， ∴CF2＝PE•BF，故 ④ 正确； ∵点 P 在运动中保持∠APB＝90°， ∴点 P 的路径是一段以 AB 为直径的弧， 如图，设 AB 的中点为 G，连接 CG 交弧于点 P，此时 CP 的长度最小， 在 Rt△BCG 中，CG＝ ， ∵PG＝ AB＝ ， ∴MN＝CP＝CG﹣PG＝ ， 即线段 MN 的最小值为 ，故 ⑤ 错误； 综上可知正确的有 4 个， 故选：C． 二、填空题（共 4 小题，每小题 3 分，满分 12 分） 15．（3 分）若 ＝ ，则 ＝ ． 【分析】直接利用已知表示出 a，b 的值，进而代入求出答案案． 【解答】解：∵ ＝ ， ∴设 a＝3x，则 b＝7x， 则 ＝ ＝ ． 故答案为： ． 16．（3 分）如图，已知圆锥的高为 8，底面圆的直径为 12，则此圆锥的侧面积是 60 π ． 【分析】圆锥的侧面积是一个扇形，根据扇形公式计算即可． 【解答】解：底面圆的直径为 12， 则半径为 6， ∵圆锥的高为 8， 根据勾股定理可知：圆锥的母线长为 10． 根据周长公式可知：圆锥的底面周长＝12 π ， ∴扇形面积＝10×12 π ÷2＝60 π ． 故答案为 60 π ． 17．（3 分）某商品售价 y（元/件）是基础价与浮动价的和，其中基础价保持不变，浮动价 与月需求量 x（件）成反比例根据表格写出 y 与 x 的函数关系式 y＝ ． 售价 y（元/件） 11 10 需求量 x（件/月） 100 120 【分析】直接根据题意假设出函数关系式进而把已知数据代入求出答案． 【解答】解：由题意设 y 与 x 的函数关系式为：y＝ +b， 则 ， 解得： ， 故 y 与 x 的函数关系式为：y＝ +5， 故答案为：y＝ +5． 18．（3 分）如图所示，n+1 个直角边长为 3 的等腰直角三角形△AB1C1，△C1B2C2……，斜 边在同一直线上，设△B2D1C1 的面积为 S1，△B3D 2C2 的面积为 S2，…，△Bn+1Dn ∁ n 的 面积为 Sn，则 S1＝ ；S2＝ 3 ；Sn＝ ． 【分析】连接 B1、B2、B3、B4、B5，则 B1B5∥AC5，通过三角形相似依次表示出 S1、S2、 S3、S4…Sn． 【解答】解：连接 B1、B2、B3、B4、B5，如图所示： ∵n+1 个直角边长为 的等腰直角三角形斜边在同一直线上， B1、B2、B3、B4、B5 的连线与直线 AC5 平行， ∵等腰直角三角形的直角边长为 3， ∴ ＝ 由题意可知，△B1C1B2 为直角边为 3 的等腰直角三角形， ∴△AC1D1∽△B2B1D1 ∴ ， S1＝ ＝ × ＝ 同理可得△B2D2B3∽△C2 D2A， ∴ ∴S2＝ ＝ × ＝3， 同理可得：△B3D3B4∽△C3D3A， ∴ ， ＝ ∴S4＝ ＝ ， … Sn＝ ＝ 故答案为： ． 三、解答题（本大题共 6 个大题，共 54 分，解答应写出文字说明、证明过程或演算步骤） 19．（8 分）已知关于 x 的一元二次方程 kx2﹣4x+2＝0 有两个不相等的实数根． （1）求实数 k 的取值范围； （2）写出满足条件的 k 的最大整数值，并求此时方程的根． 【分析】（1）利用一元二次方程的定义和判别式的意义得到 k≠0 且△＝42﹣4k•2＞0， 然后求出两不等式的公共部分即可； （2）先确定 k 的最大整数值得到方程 x2﹣4x+2＝0，然后利用因式分解法解方程即可． 【解答】解：（1）由题意得， b2﹣4ac＞0 即 42﹣4k•2＞0 解得：k＜2， 又∵一元二次方程 k≠0 ∴k＜2 且 k≠0； （2）∵k＜2 且 k 取最大整数 ∴k＝1， 当 k＝1 时，x2﹣4x+2＝0 解得，x1＝2+ ，x2＝2﹣ ． 20．（8 分）我区某中学开展“社会主义核心价值观”演讲比赛活动，九（1）、九（2）班根 据初赛成绩各选出 5 名选手参加复赛，两个班各选出的 5 名选手的复赛成绩（满分为 100 分）如图所示．根据图中数据解决下列问题： （1）九（1）班复赛成绩的中位数是 85 分，九（2）班复赛成绩的众数是 100 分； （2）小明同学已经算出了九（1）班复赛的平均成绩 ＝85 分； 方差 S2＝ [（85﹣85）2+（75﹣85）2+（80﹣85）2+（85﹣85）2+（100﹣85）2]＝70（分 2）， 请你求出九（2）班复赛的平均成绩 和方差 S22； （3）根据（2）中计算结果，分析哪个班级的复赛成绩较好？ 【分析】（1）利用众数、中位数的定义分别计算即可； （2）利用平 均数和方差的公式计算即可； （3）利用方差的意义进行判断． 【解答】解：（1）九（1）班成绩排序为：75，80，85，85，100，所以复赛成绩的中位 数是 85 分，九（2）班复赛成绩为 70，100，100，75，80，100 分出现了 2 次，所以众 数是 100 分； 故答案为：85，100； （2）九（2）班的选手的得分分别为 70，100，100，75，80， 所以九（2）班成绩的平均数 ＝ （70+100+100+75+80）＝85， 九（2）班的方差 S22＝ [（70﹣85）2+（100﹣85）2+（100﹣85）2+（75﹣85）2+（80 ﹣85）2]＝160； （3）平均数一样的情况下，九（1）班方差小， 所以九（1）班的成绩比较稳定． 21．（8 分）如图，一次函数 y＝ax+b（a≠0）的图象与反比例函数 y＝ （k≠0）的图象相 交于 A、B 两点且点 A 的坐标为（3，1），点 B 的坐标（﹣1，n）． （1）分别求两个函数的解析式； （2）求△AOB 的面积． 【分析】（1）利用待定系数法求两个函数的解析式； （2）根据三角形面积公式可得结论． 【解答】解：（1）把点 A（3，1）代入 y＝ ， 1＝ ， 解得 k＝3， ∴y＝ ， 当 x＝﹣1 时，y＝﹣3， ∴点 B（﹣1，﹣3）， 把点 A（3，1），点 B（﹣1，﹣3）代入 y＝ax+b，得 ， 解得 ， 则一次函数的解析式为：y＝x﹣2， ∴一次函数的解析式是 y＝x﹣2，反比例函数的解析式是 y＝ ， （2）由（1）知：y＝x﹣2， 当 x＝0 时，y＝﹣2， S△AOB＝S△AOC+S△BOC＝ ×|﹣2|×3+ ×|﹣2|×|﹣1|＝4． 22．（10 分）如图，点 G 是边长为 4 的正方形 ABCD 的边 BC 上的一点，矩形 DEFG 的边 EF 过点 A，GD＝5． （1）寻找并证明图中的两组相似三角形； （2）求 HG、FG 的长． 【分析】（1）根据正方形的性质和矩形的性质以及相似三角形的判定解答即可； （2）根据相似三角形的性 质解答即可． 【解答】证明：（1）∵四边形 ABCD 是正方形， ∴∠B＝∠C＝90° 又∵四边形 DEFG 是矩形 ∴∠FGD＝90° ∴∠HGB+∠DGC＝90° 又因为∠DGC +∠GDC＝90° ∴∠GDC＝∠HGB ∴△HGB∽△GDC， 相似三角形还有：△HGB∽△HAF，△DAE∽△DGC （2）在 Rt△DGC 中，∵GD＝5，DC＝4 ∴CG＝3， ∴BG＝1， ∵△HGB∽△GDC ∴ ∴HG＝ ， ∵△DGC∽△DAE， ∴ ∴DE＝ ∵四边形 DEFG 是矩形， ∴FG＝DE＝ ． 23．（10 分）随着正定旅游业的快速发展，外来游客对住宿的需求明显增大，某宾馆拥有的 床位数不断增加． （1）该宾馆床位数从 2016 年底的 200 个增长到 2018 年底的 288 个，求该宾馆这两年（从 2016 年底到 2018 年底）拥有的床位数的年平均增长率； （2）根据市场表现发现每床每日收费 40 元，288 张床可全部租出，若每床每日收费提 高 10 元，则租出床位减少 20 张．若想平均每天获利 14880 元，同时又减轻游客的经济 负担每张床位应定价多少元？ 【分析】（1）设该宾馆这两年床位的年平均增长率为 x，根据该宾馆 2016 年底及 2018 年底的床位数，即可得出关于 x 的一元二次方程，解之取其正值即可得出结论； （2）设每张床位定价 m 元，根据总价＝单价×数量，即可得出关于 m 的一元二次方程， 解之取其较小值即可得出结论． 【解答】解：（1）设该宾馆这两年床位的年平均增长率为 x， 依题意，得：200（1+x）2＝288， 解得：x1＝0.2＝20%，x2＝﹣2.2（舍去）． 答：该宾馆这两年床位的年平均增长率为 20%． （2）设每张床位定价 m 元， 依题意，得：m（288﹣20• ）＝14880， 整理，得：m2﹣184m+7440＝0， 解得 m1＝60，m2＝124． ∵为了减轻游客的经济负担， ∴x＝60． 答：每张床位应定价 60 元． 24．（10 分）如图，点 A 在数轴上对应的数为 20，以原点 O 为圆心，OA 为半径作优弧 ， 使点 B 在 O 右下方，且 tan∠AOB＝ ，在优弧 上任取一点 P，且能过 P 作直线 l∥ OB 交数轴于点 Q，设 Q 在数轴上对应的数为 x，连接 OP． （1）若优弧上一段 的长为 10 π ，求∠AOP 的度数及 x 的值． （2）若线段 PQ 的长为 10，求这时 x 的值． 【分析】（1）由 ＝10 π ，解得 n＝90°，即∠POQ＝90°，在 Rt△POQ 中，OP ＝20，tan∠PQO＝tan∠QOB＝ ，即可得出 x 的值； （2）分 PQ 在点 O 的右侧和左侧三种情况讨论求解即可． 【解答】解：（1）如图 1， 由 ＝10 π ， 解得 n＝90°， ∴∠POQ＝90°， ∵PQ∥OB， ∴∠PQO＝∠BOQ， ∴tan∠PQO＝tan∠QOB＝ ＝ ∴OQ＝ ∴x＝ ； （2）分三种情况： ① 如图 2，作 OH⊥PQ 于 H，设 OH＝ k，QH＝k．OQ＝2k， 在 Rt△OPH 中，∵OP2＝OH2+PH2， ∴202＝（ k）2+（10﹣k）2， 整理得：k2﹣5k﹣75＝0， 解得 k＝ 或 k＝ （舍弃）， ∴OQ＝2k＝ 此时 x 的值为 ② 如图 3，作 OH⊥PQ 交 PQ 的延长线于 H．设 OH＝ k，QH＝k． 在 Rt△在 Rt△OPH 中，∵OP2＝OH2+PH2， ∴202＝（ k）2+（10+k）2， 整理得：k2+5k﹣75＝0， 解得 k＝ 或 k＝ （舍弃）， ∴OQ＝2k＝ ， 此时 x 的值为﹣ +5 ③ 如图 4，作 OH⊥PQ 于 H，设 OH＝ k，QH＝k． 在 Rt△OPH 中，∵OP2＝OH2+PH2， ∴202＝（ k）2+（10﹣k）2， 整理得：k2﹣5k﹣75＝0 ， 解得 k＝ 或 （舍弃）， ∴OQ＝2k＝ 此时 x 的值为 ． 综上所述，满足条件的 x 的值为 或﹣ +5 或 ．