- 78.50 KB
- 2021-11-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
圆
一、圆的定义
定义:(1)在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一端点A随之旋转所形成的图形叫做圆,其中点O叫做圆心,OA叫做半径.
(2)圆可以看成是所有到定点O的距离等于定长r的点组成的图形.
(3)确定圆有两个要素:一是圆心;二是半径.圆心确定圆的位置,半径确定圆的大小.
(4)圆上任一点到定点(圆心)的距离都等于定长半径,到圆心的距离等于半径的点都在同一个圆上.
半径相等的圆是等圆,圆心相同的圆叫同心圆.
二、圆的概念
1. 连接圆上任意两点的线段叫做弦.
2. 经过圆心的弦叫做直径,直径长等于半径长的2倍.
3. 圆上任意两点间的部分叫做圆弧,简称弧.
(等弧指能够完全重合的两条弧,即指弧的度数和长度相等.等弧只能出现在同圆或等圆中)
4. 圆的任意一条直径的两个端点把圆分成两条弧,每一条弧叫做半圆.
5. 圆是轴对称(有无数条对称轴);又是中心对称,对称中心是圆心.
考点分析
1.圆的相关概念和性质;
2.圆中的计算;
3.圆的证明
A
C
O
B
E
D
典型例题分析与练习
类型1. 圆的有关概念
例1. 如图所示,点A、O、D以及点B、O、C分别在一条直线上,
则圆中弦的条数( )
A. 2条 B. 3条 C. 4条 D. 5条
例2. 如图在⊙O中,AB、CD为直径,请判断AD与BC的位置关系.
A
D
B
C
O
类型2. 圆中的有关计算
例1. 如图,是⊙的直径,,交⊙于,且,求的度数.
D
A
E
B
O
C
例2.一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的直径是( )
A. 2.5cm或6.5cm B. 2.5cm C. 6.5cm D. 5cm或13cm
例3. 导火索长18cm,爆破时导火索燃烧的速度是每秒0.9cm,点燃导火索的人需要跑到离爆破点120m
以外的安全区域,这个点燃导火索的人每秒跑6.5m是否安全?
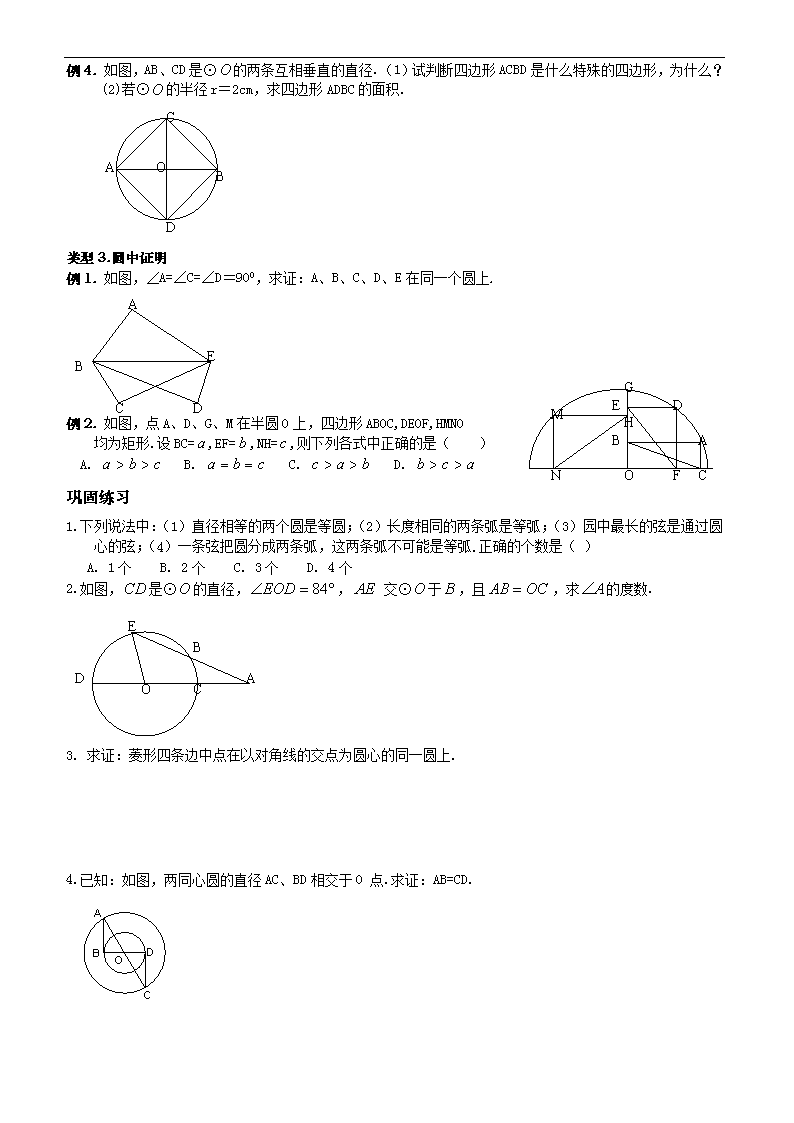
例4. 如图,AB、CD是⊙的两条互相垂直的直径.(1)试判断四边形ACBD是什么特殊的四边形,为什么?(2)若⊙的半径r=2cm,求四边形ADBC的面积.
A
D
B
C
O
类型3.圆中证明
例1. 如图,∠A=∠C=∠D=900,求证:A、B、C、D、E在同一个圆上.
A
E
B
C
D
N
O
F
C
M
B
H
E
G
D
A
例2. 如图,点A、D、G、M在半圆O上,四边形ABOC,DEOF,HMNO
均为矩形.设BC=,EF=,NH=,则下列各式中正确的是( )
A. B. C. D.
巩固练习
1.下列说法中:(1)直径相等的两个圆是等圆;(2)长度相同的两条弧是等弧;(3)园中最长的弦是通过圆心的弦;(4)一条弦把圆分成两条弧,这两条弧不可能是等弧.正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
2.如图,是⊙的直径,, 交⊙于,且,求的度数.
D
O
C
A
E
B
3. 求证:菱形四条边中点在以对角线的交点为圆心的同一圆上.
4.已知:如图,两同心圆的直径AC、BD相交于O 点.求证:AB=CD.