九年级数学下册第三章圆4确定圆的条件习题课件北师大版 32页

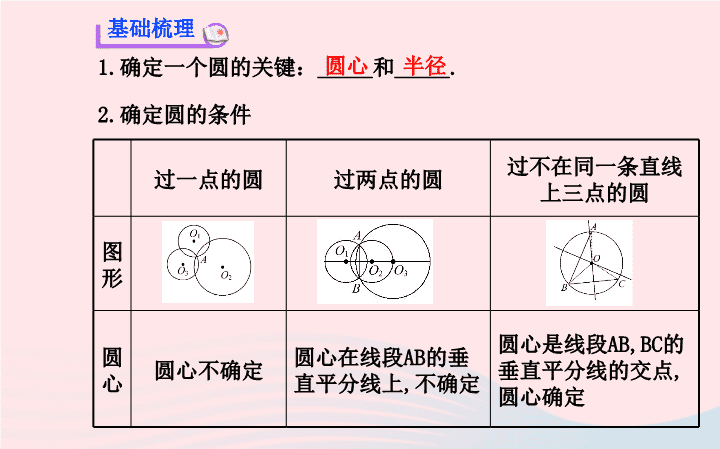
4 确定圆的条件 1. 探索平面内确定一个圆的条件 .( 重点 ) 2. 掌握过不在同一条直线上的三点作圆的方法 .( 重点、难点 ) 1. 确定一个圆的关键： _____ 和 _____. 2. 确定圆的条件 基础梳理 圆心 半径 过一点的圆 过两点的圆 过不在同一条直线上三点的圆 图形 圆心 圆心不确定 圆心在线段 AB 的垂直平分线上 , 不确定 圆心是线段 AB,BC 的垂直平分线的交点 , 圆心确定 过一点的圆 过两点的圆 过不在同一条直线上三点的圆 半径 半径不确定 半径不确定 半径 OA=OB=OC, 半径确定 总结 过一点可以作 _____ 个圆 , 过两点可以作 _____ 个圆 , 过 _______________ 的三点确定一个圆 . 过在同一直线上的三点 _____ 作圆 无数 无数 不在同一直线上 不能 3. 三角形的外接圆 三角形的 _________ 确定的圆 . 4 ．三角形的外心 (1) 定义：三角形的外接圆的 _____ ，即三角形的三边 ________ ____ 的交点 . (2) 性质：三角形的外心到三角形 ___________________. (3) 位置：锐角三角形的外心在三角形的 _____ ，直角三角形的 外心是斜边 _____ ，钝角三角形的外心在三角形的 _____ . 三个顶点 圆心 垂直平分 线 三个顶点的距离相等 内部 中点 外部 ( 打“√”或“ ×”) (1) 过三点有且只有一个圆 .( ) (2) 每个三角形都有一个外接圆 . ( ) (3) 每个圆都有惟一一个内接三角形 .( ) (4) 三角形的外心到各个顶点的距离都等于外接圆的半径 . ( ) (5) 外接圆的圆心一定在三角形的外部 .( ) × √ × √ × 知识点 1 过不在同一直线上的三点确定圆 【 例 1】 小明家的房前有一块矩形的空地， 空地上有三棵树 A,B,C ，小明想建一个圆形 花坛，使三棵树都在花坛的边上 . (1) 请你帮小明把花坛的位置画出来 ( 尺规作图，不写作法， 保留作图痕迹 ). (2) 若在△ ABC 中， AB=8 米， AC=6 米，∠ BAC=90° ，试求小明家 圆形花坛的面积 . 【 思路点拨 】 (1) 花坛即△ ABC 的外接圆，作出 AB 和 AC 的垂直平分线，其交点即为外接圆的圆心，连接圆心和一个顶点即半径 .(2) 直角三角形的外接圆的半径为斜边的一半，求出半径，再算面积 . 【 自主解答 】 (1) 用尺规作出两边的垂直平分线 , 作出圆 . ⊙O 即为所求的花园的位置 . (2)∵∠BAC=90°,AB=8 米 ,AC=6 米 ,∴BC=10 米 , ∴△ABC 外接圆的半径为 5 米 . ∴ 小明家圆形花坛的面积为 25π 平方米 . 【 总结提升 】 确定已知弧所在圆的圆心的 “ 三种 ” 方法 1. 利用圆的轴对称性，将圆对折，确定圆的两条直径，两直径的交点即为圆心 . 2. 利用圆周角定理的推论，根据 90° 的圆周角所对的弦为直径，确定直径，然后确定两直径的交点或一条直径的中点即为圆心 . 3. 根据不在同一直线上的三个点确定一个圆的方法确定圆心 . 知识点 2 与三角形的外接圆相关的计算与证明 【 例 2】 如图，在 Rt△ABC 中，∠ ACB= 90° ， AC=5,CB=12,AD 是△ ABC 的角平 分线，过 A ， C ， D 三点的圆与斜边 AB 交于点 E ，连接 DE. (1) 求证： AC=AE. (2) 求△ ACD 的外接圆的半径 . 【 解题探究 】 1.(1)DE 与 AB 有何位置关系？为什么？ 提示： DE⊥AB. ∵∠ACB=90°,∴AD 为△ ACD 的外接圆直径 , ∴∠AED=90°. (2) 结合 (1) 由 AD 平分∠ CAE ，如何证明 AC=AE ？ 提示： ∵∠ AED=90°,∠ACB=90°, AD 平分∠ CAE,∴AC=AE. 2.(1) 由已知条件和已证的结论如何求出 AE ， AB 的长度？ 提示： ∵ AC=5,CB=12, ∴AE=AC=5,BE=AB-AE=13-5=8. (2) 图中哪个三角形与△ ABC 相似？为什么？ 提示： △ ABC∽△DBE.∵AD 是直径，∴∠ AED=90° ， ∴∠ BED=∠ACB=90° ，又∵∠ B=∠B, ∴△ABC∽△DBE. (3) 由 (2) 中的三角形相似，可以得到 (4) 在△ ADE 中， 所以外接圆的半径为 【 互动探究 】 △ACD 的外接圆的面积是多少？△ ABC 的外接圆的 面积呢？ 提示： △ ACD 的外接圆的面积为 △ ABC 的外接圆的面积为 【 总结提升 】 两种三角形的外接圆半径的求法 1. 直角三角形的外心为斜边的中点，它的外接圆半径长为斜边的一半 . 2. 等腰三角形的外接圆的半径，因其底边上的中线垂直于底边，故可借助于由半径、弦的一半、圆心到弦的垂线段所组成的直角三角形求解 . 题组一： 过不在同一直线上的三点确定圆 1. 有下列四个命题：①直径是弦；②经过三个点可以作圆； ③三角形的外心到三角形各顶点的距离都相等；④半径相等 的两个半圆是等弧 . 其中正确的是 ( ) A.4 个 B.3 个 C.2 个 D.1 个 【 解析 】 选 B. 直径是圆中最长的弦，①正确；经过不在同一直线上的三点可以确定圆，②错误；三角形的外心到三角形各顶点的距离相等，③正确；半径相等的两个半圆重合，为等弧 , ④ 正确 . 2. 如图 , 在 5×5 正方形网格中 , 一条圆弧经过 A,B,C 三点 , 那么这 条圆弧所在圆的圆心是 ( ) A. 点 P B. 点 Q C. 点 R D. 点 M 【 解析 】 选 B. 作弦 AB 和 BC 的垂直平分线 , 交点 Q 即为圆心 . 3. 已知点 A,B 分别在∠ MON 的边 OM,ON 上，则经过点 A,O,B 能作圆的个数是 _________. 【 解析 】 当 0°<∠MON<180° 时，过 A,O,B 能作一个圆，当∠ MON=180° 时，不能作圆 . 故可作 0 个或 1 个圆 . 答案： 0 个或 1 个 4. 已知直线 l ： y=x+4 和点 A(0,4) ， B(-4,0) ，点 C 为直线 l 上一点，试判断点 A ， B ， C 是否在同一个圆上 . 【 解析 】 过 A ， B ， C 三点不能作一个圆 . 当 x=0 时， y=0+4=4 ；当 x=-4 时， y=-4+4=0. 故 A(0,4) ， B(-4,0) 在直线 l 上，所以 A ， B ， C 在一条直线上，所以点 A ， B ， C 不在同一个圆上 . 5. 已知 请找出 所在圆的圆心，并将圆的其他部分作出 来 . 【 解析 】 作法： (1) 在 上任取一点 C( 点 C 与 A ， B 两点不重合 ). (2) 连接 AC ， BC. (3) 分别作 AC ， BC 的垂直平分线，它们的交点 O 就是 所在圆 的圆心 . (4) 以 O 为圆心，以 OA 为半径作出⊙ O ，如图所示 . 题组二： 与三角形的外接圆相关的计算与证明 1.(2012· 雅安中考 ) 如图，已知⊙ O 是△ ABC 的外接圆，∠ AOB=110° ，则∠ C 的度数为 ( ) A ． 55° B ． 70° C ． 60° D ． 45° 【 解析 】 选 A. ∠ C 和∠ AOB 是同一条弧 AB 所对的圆周角和圆心 角，所以 【 变式备选 】 (2012· 泰州中考 ) 如图，△ ABC 内接于⊙ O ， OD⊥BC 于 D,∠A=50° ，则∠ OCD 的度数是 ( ) A ． 40° B ． 45° C ． 50° D ． 60° 【 解析 】 选 A ．连接 OB ，则∠ BOC=2∠A=100° ， OB=OC ， ∵ OD⊥BC ， ∵∠ COD ＋∠ OCD=90 ° ，∴∠ OCD=40 ° . 2.(2012 · 阜新中考 ) 如图，在△ ABC 中， BC=3 cm ，∠ BAC=60 ° ， 那么△ ABC 能被半径至少为 _____ cm 的圆形纸片所覆盖． 【 解析 】 设圆心为 O ，连接 OB,OC. 则 OB=OC ，∠ BOC=2∠BAC=120° ， 所以 则 答案： 3. 如图所示，已知 AB=5 cm,∠C=30° ，求△ ABC 的外接圆的直径 . 【 解析 】 连接 OA ， OB ， ∵∠ C=30° ，∴∠ AOB=60° ， ∵ OA =OB ， ∴△ OAB 是等边三角形， ∴ OA=AB=5 cm ， 即⊙ O 的直径为 10 cm. 4. 在△ ABC 中 ,∠ACB=90°, 斜边长为 c, 两直角边 a,b 为方程 x 2 - 19x+90=0 的根 . 求△ ABC 外接圆的面积 . 【 解析 】 ∵x 2 -19x+90=0,∴(x-9)(x-10)=0. ∴x 1 =9,x 2 =10, 即 a=9,b=10 或 a=10,b=9. ∵ 在△ ABC 中 ,∠ACB=90°, ∴c 2 =a 2 +b 2 =181, 线段 c 为△ ABC 外接圆直径 . 即△ ABC 外接圆的面积为 【 想一想错在哪？ 】 已知圆内接三角形中， AB=AC, 圆心 O 到 BC 的距离为 3 cm, 圆半径为 7 cm, 求腰长 AB. 提示： 考虑问题不全面，漏掉了△ ABC 是钝角三角形的情况 .