中考数学专题复习练习：复习：全等的识别 9页

‎（一）命题与证明 一、 命题 ‎1、命题与逆命题 ①命题：能判断正确或错误的句子。其中正确的叫 ，错误的叫 。‎ ②命题由 和 两部分组成，一般可改写为“ ”的形式。‎ ③把一个命题的 和 互相对调，得到的新命题就是它的逆命题。‎ ‎2、定理与逆定理 ①定理，是个 命题；‎ ②只有当一组互逆命题都 时，其中一个才能叫做另一个的逆定理。‎ 也就是说：（用“一定”和“不一定”填空）‎ a命题 有逆命题； b真命题的逆命题 是真命题；‎ c假命题的逆命题 是假命题； d定理 有逆定理。‎ ‎3、命题的证明 ①要说明一个命题是假命题，只需例举出 个反例即可；‎ ②要证明一个命题是真命题，则必须要有严密的推理过程；‎ 若是文字性的，还必须要① ② ③ ，然后才能证明。‎ ‎4、要求：‎ ①能判断出命题，及命题的真假；判断一组互逆命题是否是互逆定理；‎ ②能根据原命题，写出逆命题；‎ ③能证明文字性的命题。‎ 二、 证明的依据 ‎（一）总纲 图形中找，已知中寻，“隐含”条件先证明。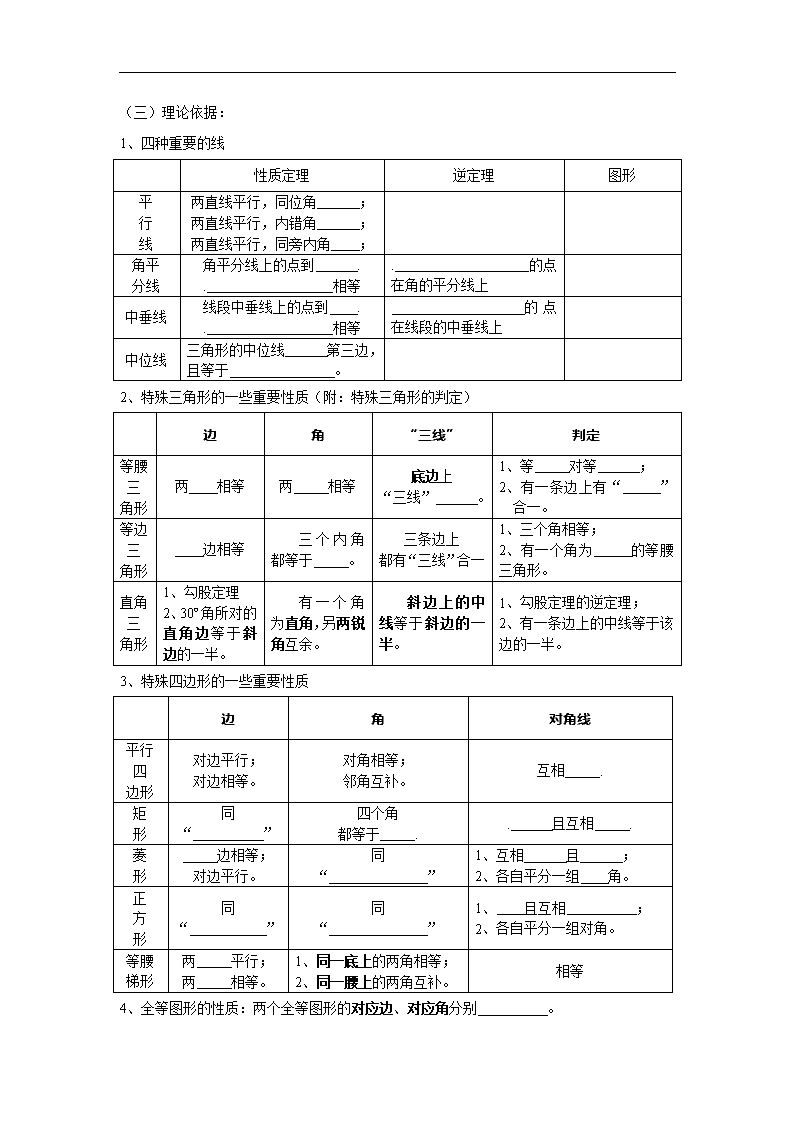‎ ‎（二）“图形”中找 ‎1、“公共边”或“对应边”中的公有部分 ‎2、“公共角”或“对应角”中的公有部分 ‎3、对顶角 ‎4、“平角”与“邻补角”‎ ‎5、三角形的“外角”‎ ‎（三）理论依据：‎ ‎1、四种重要的线 性质定理 逆定理 图形 平 行 线 两直线平行，同位角 ；‎ 两直线平行，内错角 ；‎ 两直线平行，同旁内角 ；‎ 角平 分线 角平分线上的点到 .‎ ‎. 相等 ‎. 的点在角的平分线上 中垂线 线段中垂线上的点到 .‎ ‎. 相等 ‎ 的点在线段的中垂线上 中位线 三角形的中位线 第三边，且等于 。‎ ‎2、特殊三角形的一些重要性质（附：特殊三角形的判定）‎ 边 角 ‎“三线”‎ 判定 等腰 三 角形 两 相等 两 相等 底边上 ‎“三线” 。 ‎ ‎1、等 对等 ；‎ ‎2、有一条边上有“ ”合一。‎ 等边 三 角形 ‎ 边相等 三个内角都等于 。‎ 三条边上 都有“三线”合一 ‎1、三个角相等；‎ ‎2、有一个角为 的等腰三角形。‎ 直角 三 角形 ‎1、勾股定理 ‎2、30º角所对的直角边等于斜边的一半。‎ 有一个角为直角，另两锐角互余。‎ 斜边上的中线等于斜边的一半。‎ ‎1、勾股定理的逆定理；‎ ‎2、有一条边上的中线等于该边的一半。‎ ‎3、特殊四边形的一些重要性质 边 角 对角线 平行 四 边形 对边平行；‎ 对边相等。‎ 对角相等；‎ 邻角互补。‎ 互相 .‎ 矩 形 同 ‎“ ”‎ 四个角 都等于 .‎ ‎. 且互相 .‎ 菱 形 ‎ 边相等；‎ 对边平行。‎ 同 ‎“ ”‎ ‎1、互相 且 ；‎ ‎2、各自平分一组 角。‎ 正 方 形 同 ‎“ ”‎ 同 ‎“ ”‎ ‎1、 且互相 ；‎ ‎2、各自平分一组对角。‎ 等腰梯形 两 平行；‎ 两 相等。‎ ‎1、同一底上的两角相等；‎ ‎2、同一腰上的两角互补。‎ 相等 ‎4、全等图形的性质：两个全等图形的对应边、对应角分别 。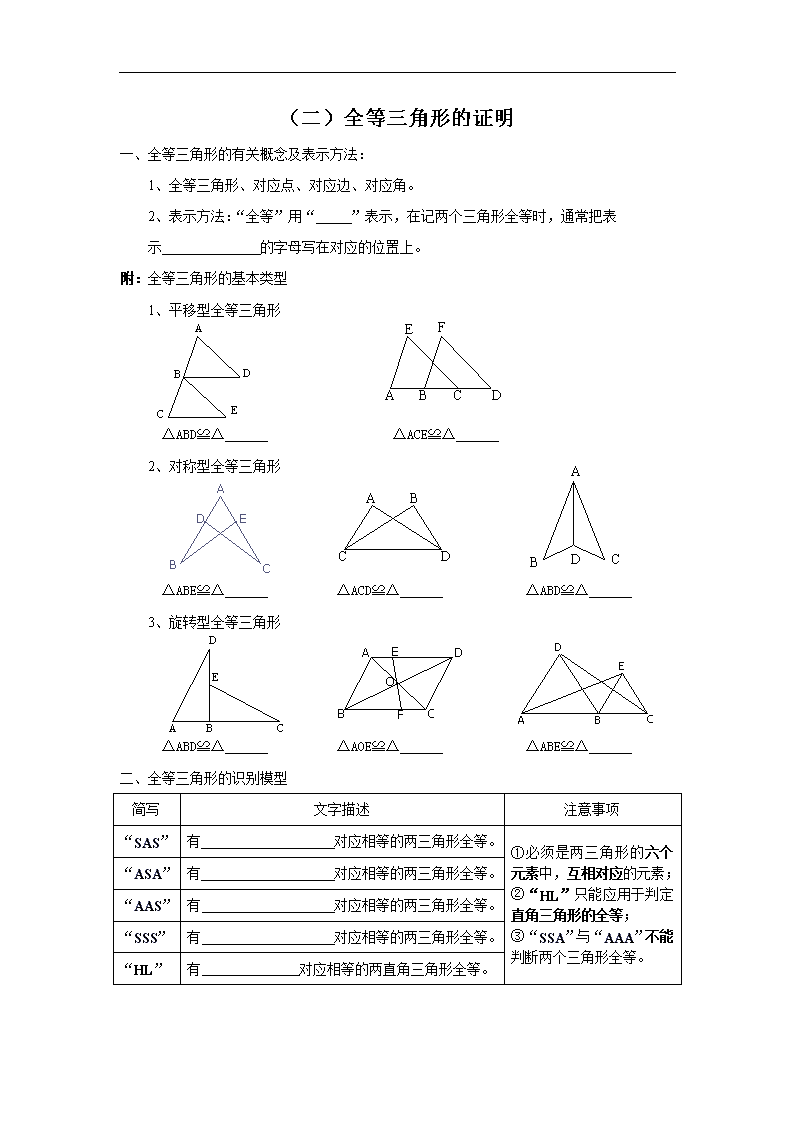‎ ‎（二）全等三角形的证明 一、全等三角形的有关概念及表示方法：‎ ‎1、全等三角形、对应点、对应边、对应角。‎ ‎2、表示方法：“全等”用“ ”表示，在记两个三角形全等时，通常把表 示 的字母写在对应的位置上。‎ 附：全等三角形的基本类型 ‎1、平移型全等三角形 ‎ △ABD≌△ △ACE≌△ ‎ ‎2、对称型全等三角形 ‎ △ABE≌△ △ACD≌△ △ABD≌△ ‎ ‎3、旋转型全等三角形 ‎ △ABD≌△ △AOE≌△ △ABE≌△ ‎ 二、 全等三角形的识别模型 简写 文字描述 注意事项 ‎“SAS”‎ 有 对应相等的两三角形全等。‎ ①必须是两三角形的六个元素中，互相对应的元素；‎ ②“HL”只能应用于判定直角三角形的全等；‎ ③“SSA”与“AAA”不能判断两个三角形全等。‎ ‎“ASA”‎ 有 对应相等的两三角形全等。‎ ‎“AAS”‎ 有 对应相等的两三角形全等。‎ ‎“SSS”‎ 有 对应相等的两三角形全等。‎ ‎“HL”‎ 有 对应相等的两直角三角形全等。‎ ‎（三）特殊四边形的判定 一、 四边形由一般到特殊的演变示意图 二、 特殊四边形的判定模型 关键点：抓住其与前面四边形的特殊性来判定。‎ 判定方法 边 角 对角线 平行 四 边形 ‎1、四边形＋ 组对边平行；‎ ‎2、四边形＋ 组对边相等；‎ ‎3、四边形＋一组对边 ；‎ ‎4、四边形＋ .‎ 组对角相等；‎ ‎5、四边形＋对角线 。‎ 矩 形 ‎1、四边形 ‎＋ 个直角；‎ ‎2、平行四边形 ‎＋ 个直角；‎ ‎3、平行四边形 ‎＋对角线 。‎ ‎★四边形＋对角 线 。‎ 菱 形 ‎1、四边形＋ 边相等；‎ ‎2、平行四边形＋ 相等；‎ ‎3、平行四边形＋对角线 ；‎ ‎4、四边形＋ 对角线平分一组对角。‎ 正方形 ‎1、矩形＋ 相等；‎ ‎2、菱形＋ .‎ 个直角；‎ ‎3、平行四边形 ‎＋对角线 ；‎ 等腰 梯形 ‎1、梯形＋ 相等；‎ ‎2、梯形＋ .‎ ‎ 两角相等 ‎3、梯形＋ 。‎ ‎（四）尺规作图 一、五种基本尺规作图方法 a) 截取一条线段等于已知线段；‎ b) 作一个角等于已知角；（理论依据是 ）‎ c) 作一个角的角平分线；（理论依据是 ）‎ d) 作一条线段的中垂线；（理论依据是 ）‎ e) 过已知点作已知直线的垂线。‎ 典 型 例 题 ‎1、（公共边）如图，已知：，。求证：。‎ ‎2、（“对应边”中的公有部分）已知：（如图）A、B、C、D在同一直线上，，且。求证：。‎ ‎3、（公共角）已知：（如图）。求证：。‎ ‎4、（平行线的性质定理及等腰三角形的判定）如图，在中，已知BO，CO分别平分和，，并且已知,。求：的周长。‎ ‎5、（角平分线的性质定理及等腰三角形的判定）已知：如图，在中，，，AD是的平分线。求证：。‎ ‎6、（中垂线性质定理的逆定理）已知：在中，M在BC上，D在AM上，‎ ‎。求证：。‎ ‎7、（等腰三角形及“对应角”中的公有部分）已知：（如图）等腰三角形ABC和等腰三角形ADE，，，且。求证：。‎ ‎8、（等边三角形）如图，已知、均为等边三角形。求证：。‎ ‎9、（直角三角形的性质及对顶角）已知：如图，AD为的高，且，F为AD上一点，连结BF并延长交AC于E，。求证：。‎ ‎10、（中垂线的性质定理及三角形的外角性质）如图，已知：AD平分，EF垂直平分AD，交BC延长线于F，连结AF。求证：。‎ ‎11、（等腰三角形的性质与判定）如图，已知：在中，，D是AB上一点，经过D作，E是垂足，并与CA的延长线相交于F。求证：。‎ ‎12、（“截长法”或“补短法”）已知：在中，，AD是的平分线。‎ 求证：。‎ ‎13、（“对应角”中的公有部分）如图，已知：。‎ 求证：。‎ 练习题 ‎1、已知：如图，。求证：。‎ ‎2、如图，已知：AB与CD相交于点O，由O画垂足为E，垂足为F，若有，。求证：。‎ ‎3、已知：（如图），，，，F为垂足。求证：。‎ ‎4、已知：如图，，。求证：。‎ ‎5、已知：（如图）。求证：AO=DO。‎ ‎6、如图，在和中，，P是BC上任意一点。求证：。‎ ‎7、如图，已知：，，且。求证：。‎ ‎8、如下图中，已知。求证：BF∥DE。‎ ‎9、如图，已知：。求证：。‎ ‎10、如图，已知：，。求证：。‎ ‎11、求证：三角形的一边的两个端点到这边的中线或中线的延长线的距离相等。‎ ‎12、如图，已知，，点E在AD上，BE平分，CE平分。求证：。‎