苏教版数学九年级上册课件1-3一元二次方程的根与系数的关系 14页

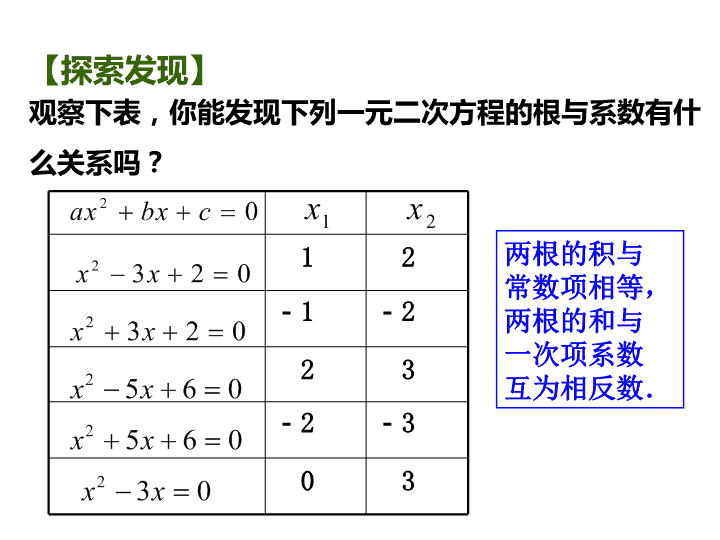
1.3一元二次方程的根与系数的 关系 【探索发现】 观察下表，你能发现下列一元二次方程的根与系数有什 么关系吗？ 1x 2x 2 3 2 0x x   2 3 2 0x x   2 5 6 0x x   2 0ax bx c   3 0 －3－2 3 2 －2－1 2 1 2 3 0x x  2 5 6 0x x   两根的积与 常数项相等， 两根的和与 一次项系数 互为相反数． 【解释规律】 你能解释刚才的发现吗？ 2 2 1 2 4 4 2 2 b b ac b b acx x a a         ， 2 2 1 2 4 4 2 2 b b ac b b acx x a a         ． 则 　　一元二次方程 ax2＋bx＋c＝0 （a≠0），如 果b2－4ac≥0，它的两个根分别是x1、x2． 2 2 1 2 4 4 2 2 b b ac b b acx x a a     ＋＋ ＝ ＋ 2 24 4 2 b b ac b b ac a      ＝ 2 2 b a ＝ b a ＝ ． 2 2 1 2 4 4 2 2 b b ac b b acx x a a       ＝  2 2 2 4 4 b b ac a  ＝ 2 4 4 ac a ＝ c a ＝ ． 【总结发现】 a bxx  21 1 2 cx x a   　如果一元二次方程ax2＋bx＋c＝0 （a≠0）， 的两个根分别x1、x2，那么： ， ． 【例题精讲】 已知方程3x2+(m+4)x+(m+1)=0的两根都是负 数,则m的值是　　　　. 【尝试与交流】 你能写出这个方程中被墨迹污染的一次项系 数和常数项吗？ 　　小明在一本课外读物中读到如下一段文字： 一元二次方程x2－ x ＝0的两根是 和 ． 2 3 2 3 【练习】 1.判断正误: (1)一元二次方程ax2+bx+c=0(a≠0)的根与系数的关 系使用的前提是b2-4ac≥0.(　　) (2)一元二次方程x2+kx-3=0的一个根是x=1,则另一 个根是-3. (　　) (1)√　(2)√ 2.若x1,x2是方程x2-3x+2=0的两根,则x1+x2的值是 (　　) A.-2　　　　B.2　　　　C.3　　　　　D.-3 C 3.若x1,x2是一元二次方程x2+4x+3=0的两根,则x1x2 的值是 (　　) A.4 B.3 C.-4 D.-3 B 4.已知方程x2-2(m2-1)x+3m=0的两个根互为相反 数,则m的值是 (　　) A.1 B.-1 C.0 D.±1 B 【小结】 2．应用一元二次方程的根与系数关系时，首先 要把方程化成一般形式； 3．应用一元二次方程的根与系数关系时， 要特别注意，方程有实根的条件，即当且仅当 b2－4ac≥0 时，才能应用根与系数的关系. 1．一元二次方程根与系数的关系是什么?