九年级数学上册第23章图形的相似23-4中位线教案新版华东师大版 5页

‎23.4　中位线 ‎1．经历三角形中位线的性质定理形成过程．‎ ‎2．掌握三角形中位线的性质定理，并能利用它解决简单的问题．‎ ‎3．通过命题的教学了解常用的辅助线的作法，并能灵活运用它们解题，进一步训练说理的能力．‎ 重点 三角形中位线的性质定理．‎ 难点 三角形中位线的性质定理的应用．‎ 一、情境引入 在前面23.3节中，我们曾解决过如下的问题：如图，在△ABC中，DE∥BC，则△ADE∽△ABC.由此可以进一步推知，当点D是AB的中点时，点E也是AC的中点，现在换一个角度考虑，如果点D，E原来就是AB与AC的中点，那么是否可以推出DE∥BC呢？DE与BC之间存在什么样的数量关系呢？‎ 二、探究新知 教师从课件展示的图片中引导学生进行猜想，证明，归纳得出三角形中位线的性质定理．‎ ‎1．猜想：从画出的图形看，可以猜想：‎ DE∥BC，且DE＝BC.‎ ‎2．证明：如图，在△ABC中，点D，E分别是AB与AC的中点，‎ ‎∴＝＝，‎ 又∵∠A＝∠A，‎ ‎∴△ADE∽△ABC(如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似)，‎ ‎∴∠ADE＝∠ABC，＝(相似三角形的对应角相等，对应边成比例)，‎ ‎∴DE∥BC，且DE＝BC.‎ 思考：本题还有其他的解法吗？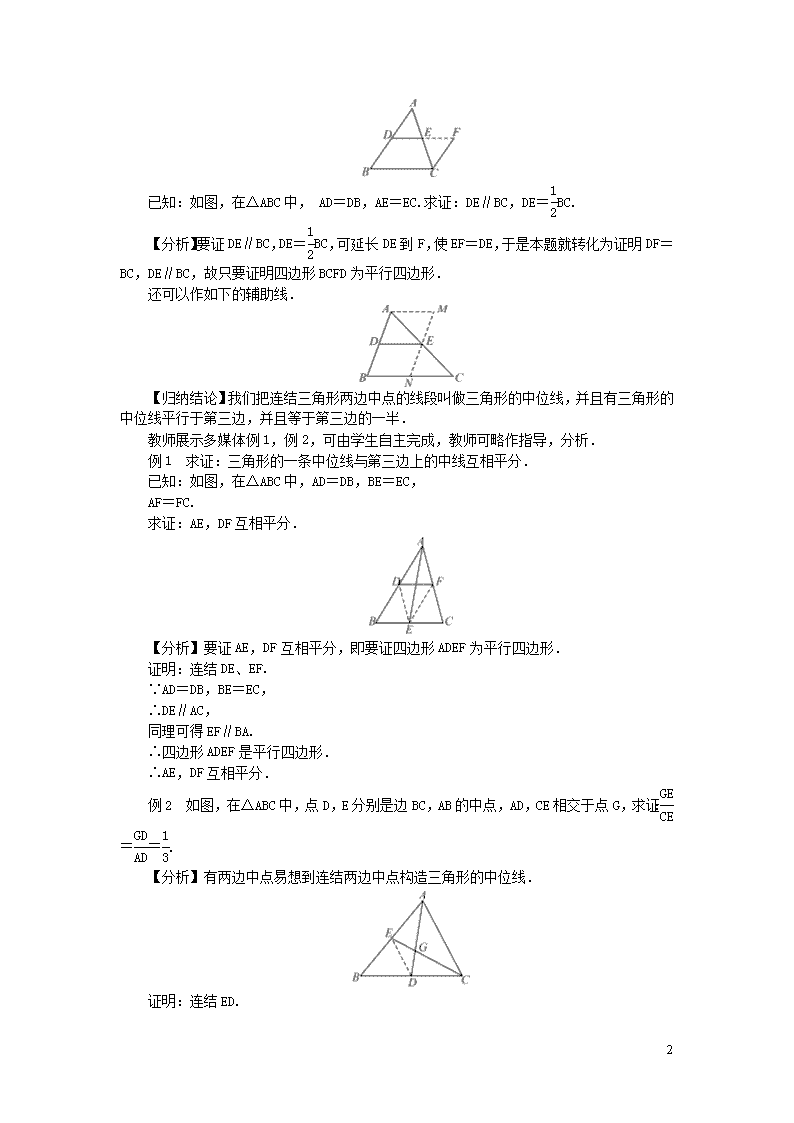‎ 5‎ 已知：如图，在△ABC中， AD＝DB，AE＝EC.求证：DE∥BC，DE＝BC.‎ ‎【分析】要证DE∥BC，DE＝BC，可延长DE到F，使EF＝DE，于是本题就转化为证明DF＝BC，DE∥BC，故只要证明四边形BCFD为平行四边形．‎ 还可以作如下的辅助线．‎ ‎【归纳结论】我们把连结三角形两边中点的线段叫做三角形的中位线，并且有三角形的中位线平行于第三边，并且等于第三边的一半．‎ 教师展示多媒体例1，例2，可由学生自主完成，教师可略作指导，分析．‎ 例1　求证：三角形的一条中位线与第三边上的中线互相平分．‎ 已知：如图，在△ABC中，AD＝DB，BE＝EC，‎ AF＝FC.‎ 求证：AE，DF互相平分．‎ ‎【分析】要证AE，DF互相平分，即要证四边形ADEF为平行四边形．‎ 证明：连结DE、EF.‎ ‎∵AD＝DB，BE＝EC，‎ ‎∴DE∥AC，‎ 同理可得EF∥BA.‎ ‎∴四边形ADEF是平行四边形．‎ ‎∴AE，DF互相平分．‎ 例2　如图，在△ABC中，点D，E分别是边BC，AB的中点，AD，CE相交于点G，求证：＝＝.‎ ‎【分析】有两边中点易想到连结两边中点构造三角形的中位线．‎ 证明：连结ED.‎ ‎∵点D，E分别是边BC，AB的中点，‎ 5‎ ‎∴DE∥AC，＝，‎ ‎∴△ACG∽△DEG，‎ ‎∴＝＝＝，‎ ‎∴＝＝.‎ 思考：在例2的图中取AC的中点F，假设BF与AD相交于点G′，如图，那么我们同理可得＝，即两图中的G与G′是重合的，由此我们可以得出什么结论？‎ 归纳：三角形三条边上的中线交于一点，这个点就是三角形的重心，重心与一边中点的连线的长是对应中线长的.‎ 三、练习巩固 教师课件展示练习题1，2，可由学生自主完成，小组内交流，再由教师点名上台展示，教师点评．‎ ‎1．如图，在▱ABCD中，点E，F分别是AD，BC上的点，且DE＝CF，BE和AF的交点为点M，CE和DF的交点为点N.求证：MN∥AD，MN＝AD.‎ ‎　第1题图 ‎　　　　　　第2题图 ‎2．如图，在四边形ABCD中，对角线AC，BD交于点O，点E，F分别是AB，CD的中点，且AC＝BD，求证：OM＝ON.‎ ‎【答案】1.解：连结EF，证四边形ABFE和四边形DCFE均为平行四边形，得FM＝AM，FN＝DN，‎ ‎∴MN∥AD，MN＝AD.‎ ‎2．解：取BC的中点G，连结EG，FG，‎ ‎∵BG＝CG，BE＝AE，‎ ‎∴GE＝AC，EG∥AC，‎ 5‎ ‎∴∠ONM＝∠GFE，‎ 同理GF＝BD，FG∥BD，‎ ‎∴∠OMN＝∠GEF，‎ ‎∵AC＝BD，‎ ‎∴GE＝GF，∴∠GEF＝∠GFE，‎ ‎∴∠ONM＝∠OMN，‎ ‎∴OM＝ON.‎ 四、小结与作业 小结 ‎1．三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．‎ ‎2．三角形中位线定理的应用．‎ ‎3．三角形重心的性质．‎ 布置作业 从教材相应练习和“习题23.4”中选取．‎ 本课时从学过的知识入手猜想中位线的性质，并通过动手画图、操作，证明猜想，体会知识的形成过程，加深对知识的理解．在证明的过程中举一反三，用多种方法证明三角形中位线定理，通过具体的实例分析，提高学生应用知识的能力．‎ 5‎ 5‎