- 785.50 KB
- 2021-11-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第
22
章:二次函数
22.1
二次函数的图像和性质
22.1.3 y=a(x-h)²+k
学习目标:
1.经历探索二次函数y=a(x-h)²+k 的图象及性质的过程,了解y=a(x-h)²+k与y=ax²、 y=ax²+k、 y=a(x-h)²的图象之间的关系。
2.会用描点法画出二次函数y=a(x-h)²+k 的图象,熟练掌握二次函数y=a(x-h)²+k 的有关性质。
3.能够灵活运用二次函数y=a(x-h)²+k 的图象和性质解决有关问题。
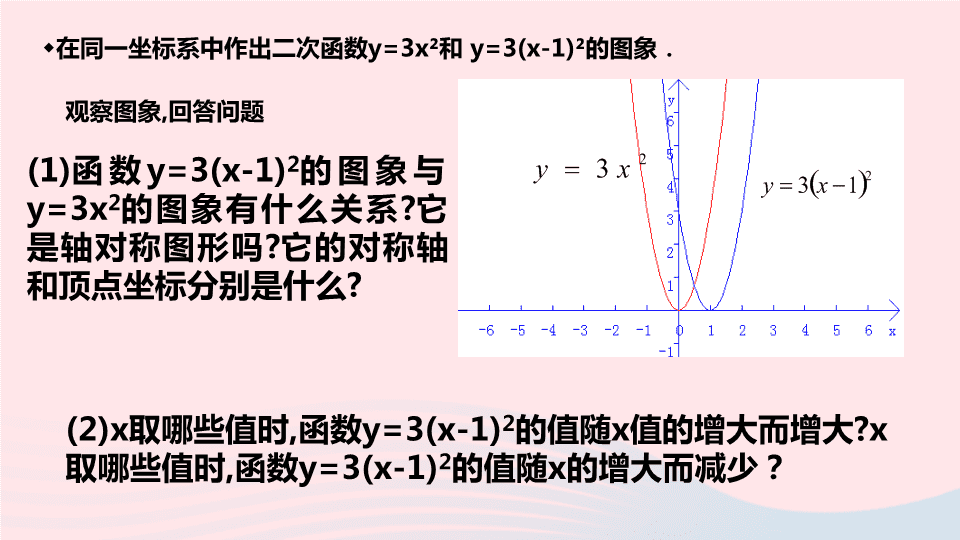
观察图象
,
回答问题
(1)
函数
y=3(x-1)
2
的图象与
y=3x
2
的图象有什么关系
?
它是轴对称图形吗
?
它的对称轴和顶点坐标分别是什么
?
(2)x
取哪些值时
,
函数
y=3(x-1)
2
的值随
x
值的增大而增大
?x
取哪些值时
,
函数
y=3(x-1)
2
的值随
x
的增大而减少?
在同一坐标系中作出二次函数
y=3x²
和
y=3(x-1)²
的图象.
二次函数
y=-0.5x
²
,
y=-0.5(x+1)
2
和
y=-0.5(x+1)
2
-1
的图象有什么关系
?
它们的开口方向
,
对称轴和顶点坐标分别是什么
?
例
3
画出函数
y=-0.5
(
x+1
)
²-1
的图像,指出它的开口方向、对称轴及顶点,抛物线
y=-0.5x²
经过怎样的变换可以得到抛物线
y=-0.5
(
x+1
)
²
-1
?
思考:
二次函数
y=-0.5(x+1)
2
-1
的
图象可以看作是抛物线
y=-0.5x
2
先沿着
x
轴向左平移
1
个单位
,
再沿直线
x=-1
向
上平移
1
个单位后得到的
.
二次函数
y=-0.5(x+1)
2
-1
的图象
和抛物线
y=-0.5x
²
,
y=-0.5(x+1)
2
有什么关系
?
它的开口方向
,
对称轴和顶点坐标分别是什么
?
y=-½(x+1)²
-1
y=-½x²
y=-½(x+1)²
对称轴仍是平行于
y
轴的直线
(x=-1);
增减性与
y=-0.5x
2
类似
.
顶点是
(-1,-1)
.
开口向下
,
当
x=-1
时
y
有
最大值
:
且
最大值是
-1.
先猜一猜
,
再
做一做
,
在同一坐标系中作二次函数
y=0.5(x+1)
2
-1,
会是什么样
?
在同一坐标系中作出二次函数
y=-3(x-1)
2
+2
,
y=-3(x-1)
2
-2,y=-3x
²
和
y=-3(x-1)
2
的图象
二次函数
y=-3(x-1)
2
+2
与
y=-3(x-1)
2
-2
和
y=-3x
²
,
y=-3(x-1)
2
的图象有什么关系
?
它们是轴对称图形吗
?
它的开口方向、对称轴和顶点坐标分别是什么
?
当
x
取哪些值时,
y
的值随
x
值的增大而增大
?
当
x
取哪些值时,
y
的值随
x
值的增大而减小
?
对称轴仍是平行于
y
轴的直线
(x=1);
增减性与
y= -3x
2
类似
.
顶点分别是
(1,2)
和
(1,-2)
.
二次函数
y=-3(x-1)
2
+2
与
y=-3(x-1)
2
+2
的图象可
以看作是抛物线
y=-3x
2
先沿着
x
轴向右平移
1
个
单位
,
再沿直线
x=1
向上
(
或向下
)
平移
2
个单位后
得到的
.
二次函数
y=-3(x-1)
2
+2
与
y=-3(x-1)
2
-2
的图象
和抛物线
y=-3x
²
,
y=-3(x-1)
2
有什么关系
?
它的开口方向
,
对称轴和顶点坐标分别是什么
?
当
x
取哪些值时,
y
的值随
x
值的增大而增大
?
当
x
取哪些值时,
y
的值随
x
值的增大而减小
?
开口向下
,
当
x=1
时
y
有
最大值
:
且
最大值
= 2
(
或最大值
=-2).
y
X=1
与
y=-3x²
有关哟
一般地
,
由
y=ax²
的图象便可得到二次函数
y=a(x-h)²+k
的图象
:
y=a(x-h)²+k(a≠0)
的图象可以看成
y=ax²
的图象先沿
x
轴整体左
(
右
)
平移
|h|
个单位
(
当
h>0
时
,
向右平移
;
当
h<0
时
,
向左平移
),
再沿对称轴整体上
(
下
)
平移
|k|
个单位
(
当
k>0
时向上平移
;
当
k<0
时
,
向下平移
)
得到的
.
因此
,
二次函数
y=a(x-h)
²
+k
的图象是一条抛物线
,
它的开口方向、对称轴和顶点坐标与
a,h,k
的值有关
.
抛物线
y=a(x-h)²+k
有如下特点:
(
1
)当
a
>
0
时,开口向上
;
当
a
<
0
时,开口向下;
(
2
)对称轴是直线
x=h
;
(
3
)顶点坐标是
(
h
,
k
)
。
二次函数
y=a(x-h)
²
+k
与
y=ax²
的关系
二次函数
y=a(x-h)
2
+k
的图象和性质
1
.
顶点坐标与对称轴
2
.
位置与开口方向
3
.
增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)
2
+k
(a>0)
y=a(x-h)
2
+k
(a<0)
(
h
,
k
)
(
h
,
k
)
直线
x=h
直线
x=h
由
h
和
k
的符号确定
由
h
和
k
的符号确定
向上
向下
当
x=-h
时
,
最小值为
k.
当
x=-h
时
,
最大值为
k.
在对称轴的左侧
,y
随着
x
的增大而减小
.
在对称轴的右侧
, y
随着
x
的增大而增大
.
在对称轴的左侧
,y
随着
x
的增大而增大
.
在对称轴的右侧
, y
随着
x
的增大而减小
.
根据图形填表:
y
x
例
4
要修建一个圆形喷水池,在池中心竖立安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线型柱在与池中心的水平距离为
1m
处达到最高,高度为
3m
,水管应多长?
点(
1
、
3
)是顶点,知道
h=1
,
k=3
,求出
a
就好啦
!
点(
3
、
0
)在抛物线上,求
a
没问题。
解:如图建立直角坐标系,点(
1
、
3
)是顶点,
设抛物线的解析式为
Y=a
(
x-1
)
²+3
(
0≤x≤3
)
点(
3
、
0
)在抛物线上,所以有
0=a
(
3-1
)
²+3
∴ a=-
∴ y=-
(
x-1
)
²+3
(
0≤x≤3
)
当
x=0
时,
y=2.25
,
即
水管应长
2.25m
。
3
4
3
4
1.
指出下列函数图象的开口方向对称轴和顶点坐标及最值
:
2.(1)
二次函数
y=3(x+1)2
的图象与二次函数
y=3x2
的图象有什么关系
?
它是轴对称图形吗
?
它的对称轴和顶点坐标分别是什么
?
(
2
)二次函数
y=-3(x-2)2
+4
的图象与二次函数
y=-3x
2
的图象有什么关系
?
3.对于二次函数
y=3(x+1)
2
,
当
x
取哪些值时
,y
的值随
x
值的增大而增大
?
当
x
取哪些值时
,y
的值随
x
值的增大而减小
?
二次函数
y=3(x+1)
2
+4
呢
?
4.
指出下列函数图象的开口方向
,
对称轴和顶点坐标
.
必要时作出草图进行验证
.
5.
填写下表
:
y=a(x-h)
²
+k
开口方向
对称轴
顶点坐标
a>0
向上
X=k
(
h
、
k
)
a<0
向下
X=k
(
h
、
k
)
相关文档
- 中考数学一轮复习知识点+题型专题2021-11-1117页
- 二次函数的图象和性质(3)(1)2021-11-113页
- 九年级数学上册第二十二章二次函数2021-11-1112页
- 中考数学三轮真题集训冲刺知识点192021-11-1114页
- 人教版九年级上册数学同步课件-第22021-11-1119页
- 华师版数学九年级下册课件-第26章 2021-11-1124页
- 九年级数学上册第二十二章二次函数2021-11-1129页
- 人教版九年级数学上册第二十二章二2021-11-1121页
- 人教版九年级上册数学同步练习课件2021-11-1116页
- 九年级数学上册第二十二章二次函数2021-11-1119页